Для получения интервалов прогноза по линейному уравнению регрессии преобразуем с учетом формул (2.5) уравнение
x = a + bx (2.22)
в уравнение
x = 
. (2.23)
Из (2.1) вытекает, что D(Y) = 
, из свойств дисперсии среднего, имеем 
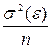. Далее, 
следовательно
D() = + 
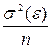s() = 
. (2.24)
Переходя от стандартного теоретического отклонения к стандартной выборочной ошибке, получаем
S() = 
= 
. (2.25)
Выберем некоторый уровень надежности g, например, равный 0,95, то есть выберем 95 % уровень надежности прогноза. Тогда доверительный интервал для расчета прогноза 
при данном значении x* рассчитывается по формуле:
, (2.26)
где tg находят по таблицам Стьюдента для заданного g и n = n - 2 (в случае парной регрессии). Так, например, при n = 10 и g = 0,95 по таблице приложений 1, получаем tg = 2,306. В нашем примере 
, следовательно, 
0,5621. Далее,
S() = =0,5621 × 
Получаем окончательную формулу для интервала прогноза :
[0,924+0,658 ×x- 1,2962 × ; 0,924+0,658 *x+ +1,2962× ].
Построим соответствующие графики, используя возможности пакета STATISTICA на участке [0 ¸ 15].
Рис. 2.3
2.5. Контрольные вопросы и варианты лабораторной работы «Парный регрессионный анализ»
1. Как выглядит линейная модель парной регрессии? Как называют переменные участвующие в модели?
2. Почему существуют отклонения от теоретической прямой линии регрессии?
3. Выведите формулы для расчета коэффициентов прямой парной регрессии по МНК.
4. Сформулируйте условия Гаусса-Маркова в методе МНК.
5. Приведите формулу расчета коэффициента детерминации R2 и объясните его роль при определении качества построенного уравнения регрессии.
6. Как производится проверка значимости уравнения регрессии по F-критерию Фишера?
|
|
7. Выведите формулы, связывающие теоретические коэффициенты модели a и b с МНК коэффициентами a и b и докажете несмещенность МНК оценок.
8. Выведите формулы для дисперсий и стандартных отклонений МНК оценок. Покажите, что из этих формул следует состоятельность МНК оценок.
9. Опишите алгоритм проверки значимости коэффициентов a и b с использованием стандартных выборочных ошибок коэффициентов и критерия Стьюдента.
10. Как строятся доверительные интервалы для прогноза Y по линейному уравнению регрессии? Какой выбирается уровень надежности прогноза? От каких факторов зависит ширина интервала прогноза?
Проведите парный регрессионный анализ с использованием пакета STATISTICA по данным своего варианта (см. табл. 2.6).
Таблица 2.6
Данные для проведения лабораторной работы по теме
«Парный регрессионный анализ»
| № | Y1 | Y2 | Y3 | Y4 | Y5 | Y6 | Y7 | Y8 | Y9 | Y10 |
| 1,26 | 1,73 | 1,34 | 1,48 | ,34 | 2,26 | 3,82 | 1,34 | ,678 | 2,41 | |
| 2,16 | 1,87 | 1,65 | 1,53 | 1,54 | 2,38 | 4,11 | 3,08 | ,78 | 2,48 | |
| 2,17 | 2,54 | 2,67 | 2,34 | 1,65 | 2,95 | 5,48 | 2,64 | ,83 | 3,33 | |
| 2,68 | 2,88 | 2,75 | 3,33 | 2,68 | 4,23 | 6,77 | 4,26 | 1,71 | 4,45 | |
| 3,17 | 2,47 | 3,16 | 3,38 | 2,77 | 4,81 | 7,48 | 4,78 | 1,38 | 5,12 | |
| 3,81 | 3,40 | 3,87 | 4,40 | 2,89 | 6,04 | 8,04 | 5,49 | 1,98 | 6,46 | |
| 3,59 | 3,64 | 3,95 | 4,79 | 3,50 | 6,21 | 8,79 | 6,84 | 1,67 | 7,15 | |
| 4,02 | 4,00 | 4,88 | 5,03 | 2,96 | 7,02 | 9,62 | 7,48 | 1,99 | 7,74 | |
| 4,43 | 3,87 | 4,49 | 6,02 | 3,16 | 7,70 | 10,54 | 9,57 | 2,18 | 8,50 | |
| 4,90 | 4,53 | 4,62 | 6,65 | 2,94 | 8,77 | 11,48 | 9,19 | 2,55 | 9,29 | |
| 5,701 | 4,76 | 5,91 | 8,01 | 3,21 | 9,06 | 12,81 | 9,91 | 2,87 | 10,33 | |
| 6,02 | 5,07 | 7,29 | 7,22 | 4,28 | 10,05 | 13,28 | 12,29 | 2,85 | 10,89 | |
| 5,92 | 5,04 | 7,26 | 7,92 | 4,20 | 10,97 | 14,42 | 12,39 | 3,24 | 12,35 | |
| 6,42 | 5,64 | 6,92 | 9,23 | 5,35 | 12,61 | 15,28 | 11,67 | 3,30 | 12,46 | |
| 7,32 | 5,72 | 7,85 | 9,43 | 5,38 | 12,88 | 16,14 | 13,23 | 3,16 | 13,07 | |
| 7,44 | 5,75 | 8,15 | 10,37 | 5,93 | 13,35 | 17,79 | 14,38 | 3,52 | 13,48 | |
| 8,44 | 6,32 | 8,63 | 10,56 | 5,45 | 14,98 | 17,45 | 16,06 | 3,88 | 14,98 | |
| 8,34 | 6,75 | 9,59 | 11,25 | 5,44 | 15,38 | 19,26 | 16,42 | 3,97 | 15,72 | |
| 9,06 | 6,88 | 10,23 | 11,68 | 6,52 | 16,04 | 19,59 | 17,44 | 4,64 | 16,02 | |
| 9,19 | 7,42 | 10,97 | 12,15 | 7,20 | 16,80 | 20,60 | 18,46 | 4,72 | 16,83 |
|
|
Лабораторная работа № 1 «Модель парной линейной регрессии»
По имеющимся данным
1. Вычислить дескриптивные (описательные) статистики:
1) выборочные средние;
2) выборочную дисперсию;
3) выборочное среднее квадратичное отклонение;
4) нижний и верхний квартили выборочного распределения;
5) размах выборки;
6) 95 % и 99 % доверительные интервалы для оценки математического ожидания (и дисперсии) в предположении, что выборочные данные имеют нормальное распределение.
2. Вычислить выборочный коэффициент корреляции и оценить его значимость на 5 % уровне.
3. Построить корреляционное поле заданных переменных и сформулировать гипотезу о виде связи.
4. Вычислить параметры уравнения парной регрессионной модели.
5. Оценить значимость построенного уравнения регрессии с помощью F-критерия.
6. Оценить качество построенного уравнения регрессии с помощью коэффициента детерминации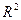 
.
7. Построить 95 % -ные интервалы для оценок параметров уравнения регрессии.
8. Рассчитать прогнозное значение, если значение независимой переменной увеличится на 10 % от его среднего значения. Построить 95 % доверительный интервал для прогнозного значения.
9. Оценить с помощью коэффициента эластичности (среднего) силу связи независимой переменной с зависимой.
10. Рассчитать параметры уравнений регрессий других форм: степенной, логарифмической, экспоненциальной и др.
|
|
Таблица 2.7
 |
Исходные данные