Проблема мультиколлинеарности факторов

Под мультиколлинеарностью понимается высокая степень коррелированности объясняющих переменных. Крайний случай мультиколлинеарности – это случай линейной зависимости между столбцами информационной матрицы Х. При этом определитель матрицы равен 0 и не существует обратной матрицы С = ()^-1. Расчет коэффициентов модели по МНК в этом случае невозможен. Гораздо чаще в экономических исследованиях встречается стохастическая мультиколлинеарность. В этом случае корреляционная связь между факторами высокая, определитель матрицы мал и, следовательно, велики элементы, в том числе диагональные, матрицы С = ()^-1. Эти элементы входят в формулы для расчета дисперсии коэффициентов модели и дисперсии расчетного и наблюдаемого значений зависимой переменной. Качество модели падает, так как модель становится чувствительной к незначительным изменениям в величине и объеме данных. Прогноз по такой модели теряет смысл, а коэффициенты могут не отвечать требованиям теоретических предпосылок.

Рассмотрим следующий пример. Пусть точное уравнение, связывающее зависимую переменную с тремя объясняющими переменными, имеет вид:

(3.38)

Прибавим к точным значениям ошибку наблюдения d, получим наблюдаемые значения зависимой переменной . Данные наблюдений отражает табл. 3.8.

Таблица 3.9

X1	X2	X3		d	y
1,1	1,1	1,2	25,40	0,8	26,20
1,4	1,5	1,1	26,40	-0,5	25,90
1,7	1,8	2,0	32,10	0,4	32,50
1,7	1,7	1,8	30,80	-0,5	30,30
1,8	1,9	1,8	31,50	0,2	31,70
1,8	1,8	1,9	31,70	1,9	33,60
1,9	1,8	2,0	32,30	1,9	34,20
2,0	2,1	2,1	33,80	0,6	34,40
2,3	2,4	2,5	37,00	-1,5	35,50
2,5	2,5	2,4	37,00	-0,5	36,50

Переменные X1, X2, X3 сильно коррелируют друг с другом ().

Метод наименьших квадратов для наблюдаемой переменной y приводит к уравнению

(3.39)

Различие в моделях (3.38) и (3.39) очевидно. Поменялся даже знак коэффициента при x2, что приводит к неверным выводам даже в качественном, а не только в количественном описании взаимодействия факторов с выходной переменной. Использование модели (3.39) невозможно.

Различные методы, которые могут быть использованы для смягчения мультиколлинеарности делятся на две категории. К первой категории относятся методы уменьшающие дисперсию оценок. К таким методам относятся: радикальное увеличение числа опытов; отбор из множества объясняющих переменных тех переменных, которые имеют наиболее низкие взаимные коэффициенты корреляции;на стадии подготовки данных следует максимизировать дисперсию наблюдений независимых переменных путем расслоения выборки; уменьшить дисперсию остатков путем введения упущенной в первоначальной модели важной переменной.

Второй способ смягчения мультиколлинеарности: использование внешней информации о структуре модели и ввод ограничений на величину оценок или виде связи между коэффициентами модели.

Еще один способ устранения мультиколлинеарности: переход от несмещенных оценок МНК с большой дисперсией, к смещенным оценкам но с гораздо меньшей дисперсией. В результате доверительный интервал той же длины для смещенного коэффициента будет накрывать истинный коэффициент с большей вероятностью. Метод построения модели использующий эту идею называется методом гребневой регрессии (ридж-регрессии). В этом методе расчет коэффициентов модели проводят по формуле

где - некоторое подбираемое исследователем положительное число, называемое «гребнем», а - единичная матрица к +1–го порядка. Величина выбирается из условий компромисса между желанием уменьшить - смещенность оценки b и уменьшить ее дисперсию за счет увеличения определителя матрицы .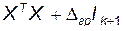

Наконец, можно провести преобразование исходных данных и получить новые ортогональные факторы, называемые главными компонентами, и получить уравнение регрессии. Этот метод называется регрессией на главные компоненты.

Метод главных компонент

Основная идея метода заключается в замене сильно коррелированных переменных совокупностью новых переменных, между которыми корреляция отсутствует. При этом новые переменные являются линейными комбинациями исходных переменных:

Переменные называют главными компонентами. Будем подбирать их так, чтобы имела бы наибольшую дисперсию. Для каждой следующей компоненты дисперсия убывает, а последняя компонента будет иметь наименьшую дисперсию. Можно предполагать, что исходные переменные уже стандартизированы, так что все переменные имеют нулевое математическое ожидание и единичную дисперсию. При этом матрица является корреляционной матрицей для исходных данных.

Для первой главной компоненты где , справедливы равенства M(z₁) = ; .

Хорошо известно, что невырожденная корреляционная матрица имеет m положительных собственных значений и m соответствующих им собственных векторов.

Пусть собственный вектор матрицы , а l₁ соответствующее этому собственному вектору собственное значение, то есть 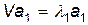. Умножая последнее равенство слева на 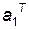, получаем . Чтобы вектор однозначно определить, дополнительно потребуем, чтобы . Тогда и проблема нахождения первой главной компоненты с максимальной дисперсией решается путем нахождения наибольшего собственного значения и соответствующего ему собственного вектора корреляционной матрицы .

Рассуждая аналогично, находим вторую главную компоненту при условиях нормировки и линейной независимости (ортогональности векторов) . Дисперсия второй главной компоненты будет равна второму по величине собственному значению l₂ матрицы . Проверим, что главные компоненты и не коррелируют между собой. В самом деле

Продолжая процесс построения, получаем систему главных компонент, не коррелирующих друг с другом, с дисперсиями равными собственным числам корреляционной матрицы . Так как исходные переменные были сильно коррелированны, то матрица плохо обусловлена, то есть ее определитель близок к нулю. С другой стороны можно показать, что определитель . Следовательно, можно ожидать, что одно или несколько последних собственных значений матрицы достаточно малы. Тогда, отбросив соответствующие главные компоненты, мы получаем возможность сократить размерность задачи, уменьшить число факторов в модели.

Применим метод главных компонент к рассмотренному выше примеру табл. 3.4.

Составим корреляционную матрицу С, и посчитаем собственные векторы и собственные значения матрицы С используя, например, пакет МАТКАД

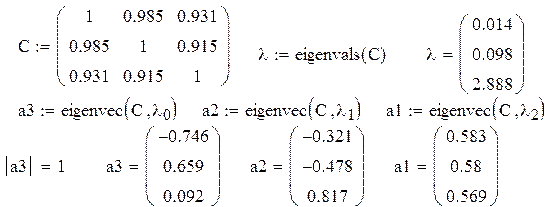
Первая главная компонента имеет вид

. (3.40)

Аналогично вычисляются и остальные главные компоненты. Коэффициенты корреляции между y и главными компонентами , , равны Это еще раз подтверждает, что почти вся информация о линейной связи между y и сводится к информации о связи между y и первой главной компонентой . Если написать уравнение регрессии, связывающее переменную y и , а затем перейти, используя (3.40), к исходным переменным в естественной, а не в стандартизированной форме, то получим окончательное уравнение:

(3.41)

Уравнение (3.41) правильно отражает качественные свойства зависимостей и значительно ближе к точному уравнению (3.39), чем классическое МНК уравнение (3.40).