Частный  -критерий предназначенный для включения фактора в модель сравнивает прирост факторной дисперсии за счет дополнительно включенного фактора с остаточной дисперсией приходящейся на одну степень свободы по регрессионной модели в целом.
-критерий предназначенный для включения фактора в модель сравнивает прирост факторной дисперсии за счет дополнительно включенного фактора с остаточной дисперсией приходящейся на одну степень свободы по регрессионной модели в целом.
 . (3.34)
. (3.34)
Величина  показывает долю вариации y объясненную регрессией за счет введения фактора xi,
показывает долю вариации y объясненную регрессией за счет введения фактора xi,  - это доля остаточной вариации модели включающей полный набор факторов. Если числитель и знаменатель (3.34) умножить на
- это доля остаточной вариации модели включающей полный набор факторов. Если числитель и знаменатель (3.34) умножить на  , то получим отношение не долей, а отношение прироста факторной объясняющей суммы квадратов отклонений к остаточной сумме квадратов. Так как прирост факторной суммы квадратов обусловлен включением в модель одного фактора, то число степеней свободы для него равно
, то получим отношение не долей, а отношение прироста факторной объясняющей суммы квадратов отклонений к остаточной сумме квадратов. Так как прирост факторной суммы квадратов обусловлен включением в модель одного фактора, то число степеней свободы для него равно  .
.
Для остаточной суммы квадратов 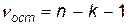 .Фактическое значение частного
.Фактическое значение частного  -критерия сравнивается с табличным при некотором уровне значимости
-критерия сравнивается с табличным при некотором уровне значимости  . Если наблюдаемый
. Если наблюдаемый  -критерий превышает табличное значение, то фактор признают значимым и оставляют в модели, если наблюдаемый
-критерий превышает табличное значение, то фактор признают значимым и оставляют в модели, если наблюдаемый  -критерий меньше табличного, то фактор признается незначимым и принимается гипотеза
-критерий меньше табличного, то фактор признается незначимым и принимается гипотеза  Аналогичную процедуру можно применять и для усложнения модели путем решения вопроса о включении в нее нового фактора. В пакетах прикладных программ, например, в пакете STATISTICA реализованы как процедура включения, так и процедура исключения фактора из модели. Пользователь определяет сам критические значения критериев для включения и исключения факторов
Аналогичную процедуру можно применять и для усложнения модели путем решения вопроса о включении в нее нового фактора. В пакетах прикладных программ, например, в пакете STATISTICA реализованы как процедура включения, так и процедура исключения фактора из модели. Пользователь определяет сам критические значения критериев для включения и исключения факторов  и
и  .
.
В методе исключения анализ начинается с включения в регрессионную модель всех переменных. Затем для каждой переменной вычисляют частную F-статистику и ту переменную, для которой F-статистика минимальна, исключают из рассмотрения. Затем строится новая модель по оставшимся переменным и после вычисления частных F-статистик вновь удаляют одну из переменных и т.д. Так поступают до тех пор, пока не будет достигнуто заранее заданное число переменных в модели или F-статистики не станут все больше заданного порога.
В методе включения начинают с построения модели, включающей лишь одну переменную, имеющую наибольший по абсолютной величине парный коэффициент корреляции с переменной выхода. Затем вычисляют частные F-статистики для всех оставшихся переменных и включают в модель переменную с наибольшей F-статистикой. Это эквивалентно включению переменной имеющей наибольший частный коэффициент корреляции с переменной выхода. Процесс продолжают до достижения в модели определенного числа переменных или F-статистики не станут меньше заданного порога.
Более сложной процедурой является комбинация методов включения и исключения. Выбираются фиксированные пороговые уровни  и
и  и на каждом шаге рассматриваются следующие возможности: добавить переменную, исключить переменную, одну переменную заменить другой, остановить процесс. На каждом шаге вычисляются F-статистики переменных, величина
и на каждом шаге рассматриваются следующие возможности: добавить переменную, исключить переменную, одну переменную заменить другой, остановить процесс. На каждом шаге вычисляются F-статистики переменных, величина  и степень допустимой коррелированности переменных, вошедших в регрессионное уравнение, которая вычисляется по формуле Т =
и степень допустимой коррелированности переменных, вошедших в регрессионное уравнение, которая вычисляется по формуле Т =  . Обычно задают уровень Тдопуска = 0,01,
. Обычно задают уровень Тдопуска = 0,01,  , и
, и  подбирают в ходе решения задачи. Переменную с максимальным значением F включают в модель при условии, что значения Т не превышают Тдопуска (степень коррелированности системы не должна быть слишком большой), но при этом F >
подбирают в ходе решения задачи. Переменную с максимальным значением F включают в модель при условии, что значения Т не превышают Тдопуска (степень коррелированности системы не должна быть слишком большой), но при этом F >  ;если оказывается, что F <
;если оказывается, что F <  , то переменную исключают из модели.
, то переменную исключают из модели.
Преимуществом шаговых методов являются простота алгоритмов, автоматизация выбора наилучшей модели, быстрота вычислений; недостатком — раздельный анализ переменных (по отдельности переменные могут не являться значимыми, но при совместном использовании улучшают показатели регрессионной модели).
Другой способ пошагового отбора факторов состоит в использовании скорректированного (adjusted) коэффициента детерминации, определяемого по формуле
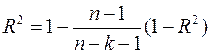 . (3.35)
. (3.35)
В отличие от обычного коэффициента детерминации  , который всегда увеличивается при добавлении новых факторов, скорректированный коэффициент детерминации может уменьшаться при добавлении новых переменных не оказывающих существенное влияние на выходную переменную y. Однако даже увеличение скорректированного) коэффициента детерминации не всегда означает, что вводимый в модель фактор значим. Поэтому, описанный выше метод шаговой регрессии, основанный на использовании
, который всегда увеличивается при добавлении новых факторов, скорректированный коэффициент детерминации может уменьшаться при добавлении новых переменных не оказывающих существенное влияние на выходную переменную y. Однако даже увеличение скорректированного) коэффициента детерминации не всегда означает, что вводимый в модель фактор значим. Поэтому, описанный выше метод шаговой регрессии, основанный на использовании  и
и  предпочтительнее.
предпочтительнее.
Рассмотрим пример. В табл. 3.2 представлены данные для исследования зависимости урожайности семян люцерны от следующих факторов:
1) x1 - количество осадков в период сентябрь -20 апреля (мл);
2) x2 - количество осадков в период 20 апреля -20 мая (мл);
3) x3 -температура воздуха в фазе цветения (С0);
4) x4 -относительная влажность воздуха в фазе цветения (%);
5) x5 -количество осадков в фазе цветения (мл);
6) x6 -температура почвы на глубине 20 см 20 мая (С0);
7) x7 -высота растения 20 мая (мм).
В табл. 3.2 представлены данные 12 опытов, проведенных в 1986 - 1989 гг. в учхозе «Березовский» Воронежского агроуниверситета.
С целью выбора наилучшего варианта набора переменных применим комбинированный вариант включения и исключения неизвестных в процедуре шаговой регрессии реализованный в модуле «Множественная регрессия» пакета STATISTICA.
Таблица 3.2
| Номер опыта | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
| 17,3 | 65,3 | 65,4 | |||||
| 20,2 | |||||||
| 18,9 | 131,6 | ||||||
| 18,8 | 55,1 | ||||||
| 18,1 | 171,9 | ||||||
| 62,1 | 46,6 | ||||||
| 73,2 | 95,7 | ||||||
| 17,3 | 66,3 | 119,7 | |||||
| 17,3 | 65,3 | 65,4 | |||||
| 17,3 | 66,3 | 149,1 | |||||
| 69,3 | |||||||
Дополним множество переменных следующими переменными  ,
,  ,
, 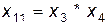 ,
,  ,
,  ,
,  . Матрицу данных зададим в табл. 3.3.
. Матрицу данных зададим в табл. 3.3.
Таблица 3.3

Рассчитаем частные коэффициенты корреляции (Partial Correlations) и значения частной F-статистики (F –to enter/ to remove) на каждом шаге регрессии. Всего было задано пять шагов регрессии при  = 1,15 и
= 1,15 и  = 1. Результаты расчетов представлены в таблицах 3.4 - 3.6.
= 1. Результаты расчетов представлены в таблицах 3.4 - 3.6.
Таблица 3.4
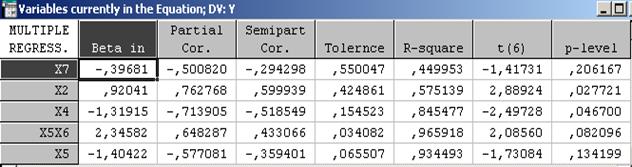
Таблица 3.5

Таблица 3.6

Результаты расчетов показывают, что хотя некоторые переменные x5, x5x6 имеют незначимые уровни значимости (p-level >0,05), но их желательно оставить в уравнении регрессии, так как при их включении прирост коэффициента детерминации R2 составил 0,193364, то есть 20 % всего возможного диапазона изменения R2.
Выпишем полученное уравнение, сначала используя исходные переменные:
 (3.36)
(3.36)
Напомним, что
x2 - количество осадков в период 20 апреля - 20 мая (мл);
x4 - относительная влажность воздуха в фазе цветения (С0);
x5 - количество осадков в фазе цветения (мл);
x6 - температура почвы на глубине 20 см 20 мая (С0);
x7 - высота растения 20 мая (мм).
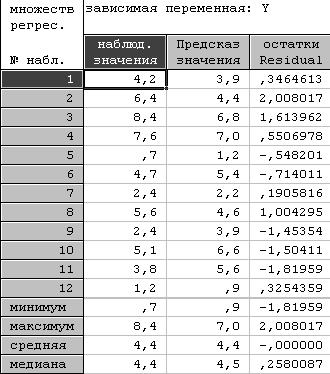
Составим табл. 3.7 наблюдаемых, расчетных значений и остатков урожайности семян люцерны.
Качество предсказания получилось посредственное, средняя абсолютная ошибка предсказания равна 1,0, а средняя относительная ошибка равна почти 30 %.
Рассмотрим вопрос о ранжировании факторов по силе их влияния на формирование урожая. Для этого надо переписать уравнение (3.36) через стандартизированные факторы, то есть факторы вида 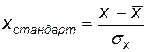 .
.
Таблица 3.7
Тем более, что в пакете STATISTICA коэффициенты модели со стандартизированными факторами приводятся в столбце BETAтаблицы REGRESSION SUMMARY. Стандартизированный коэффициент регрессии  показывает на сколько величин
показывает на сколько величин  изменится в среднем зависимая переменная y при увеличении переменной
изменится в среднем зависимая переменная y при увеличении переменной 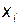 на
на  . Имеем
. Имеем
 . (3.37)
. (3.37)
Из свойств уравнения в стандартизированных переменных заключаем, что наибольшее влияние на выходную переменную при изменении каждого фактора xi на величину  окажет фактор
окажет фактор 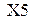 в отдельности и в сочетании факторов
в отдельности и в сочетании факторов  . Следующий по силе влияния - фактор
. Следующий по силе влияния - фактор  , затем фактор
, затем фактор  и, наконец, фактор
и, наконец, фактор  .
.
По уравнению (3.37) можно ранжировать факторы по силе влияния на y, но количественно сравнить силу этого влияния можно используя коэффициенты эластичности модели  . Коэффициенты эластичности показывают: на сколько процентов от среднего значения изменится зависимая переменная y при увеличении переменной
. Коэффициенты эластичности показывают: на сколько процентов от среднего значения изменится зависимая переменная y при увеличении переменной 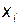 на 1 %. Вычислим коэффициенты эластичности каждого фактора. Для этого вычислим в модуле Basic Statistic пакета STATISTICA средние факторов и зависимой переменной y. Имеем
на 1 %. Вычислим коэффициенты эластичности каждого фактора. Для этого вычислим в модуле Basic Statistic пакета STATISTICA средние факторов и зависимой переменной y. Имеем
Таблица 3.8
| Факторы | Средние | Факторы | Средние |
| X1 | 358,50 | X1X2 | 26806,33 |
| X2 | 69,08 | X2X3 | 1321,17 |
| X3 | 18,85 | X3X4 | 1282,14 |
| X4 | 67,98 | X4X5 | 7126,24 |
| X5 | 102,13 | X5X6 | 1557,70 |
| X6 | 16,42 | X6X7 | 938,42 |
| X7 | 58,33 | Y | 4,37 |
Отсюда
 -0,06034*102,13/4,37=-1,4101886;
-0,06034*102,13/4,37=-1,4101886;
 0,00919*1557,70/4,37=3,2758039;
0,00919*1557,70/4,37=3,2758039;
 -0,68161*67,98/4,37=-10,6031688;
-0,68161*67,98/4,37=-10,6031688;
 0,07299*69,08/4,37=1,1538099;
0,07299*69,08/4,37=1,1538099;
 -,06971*58,33/4,37=-0,930477.
-,06971*58,33/4,37=-0,930477.