Опыт использования методов регрессионного анализа показывает, что для адекватного описания объекта исследования необходимо удачно выбрать предсказывающие переменные. Например, для успешного прогнозирования урожайности нужно выбрать наиболее информативные агрометеорологические, почвенные и социально-технологические факторы. При этом у исследователя обычно имеется в распоряжении несколько десятков факторов, реально влияющих на сельскохозяйственные культуры. Однако модель, построенная по всем факторам, как правило, имеет плохие прогнозирующие свойства.
Ранее отмечалось, что для оценки качества модели можно использовать коэффициент детерминации 
, который численно выражает долю дисперсии переменной выхода, объясненную с помощью регрессионного уравнения. Однако для получения наилучшего набора переменных этот коэффициент мало пригоден.
Во-первых, при включении новой переменной в модель коэффициент детерминации либо остается практически неизменным, либо увеличивается. Во-вторых, зависит от крутизны поверхности регрессии. В одномерном случае при увеличении угла наклона прямой регрессии к оси абсцисс величина может быть близка к единице при плохом качестве прогноза по уравнению регрессии. Наконец,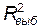 
является смещенной оценкой для 
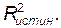При 
математическое ожидание 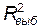равно: 
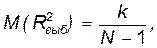где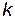 
— число переменных в регрессионной модели, а 
— число наблюдений. Поэтому при значениях 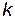, близких к объему выборки можно получить значение 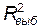близкое к единице, хотя 
Все это заставляет искать другие критерии для поиска наилучшего набора переменных регрессионной модели.
Рассмотрим показатель статистической связи между двумя переменными, называемый частным коэффициентом корреляции. Во многих задачах, в том числе экономических, агрометеорологических факторы, как правило, сильно коррелируют и трудно выделить «чистое» влияние на переменную выхода каждой независимой переменной. С целью выделения этого влияния и вычисляют частный коэффициент корреляции, как меру линейной связи между зависимой переменной Y и какой-либо одной из переменных 
после удаления влияния на эту связь всех остальных переменных.
|
|
Укажем один из способов построения частного коэффициента корреляции. Пусть, например, изучается линейная связь между переменными 
и требуется найти коэффициент корреляции между зависимой переменной 
и независимой переменной 
, «очищенный» от влияния переменной 
.
Вычислим парные коэффициенты корреляции 
и рассмотрим разность
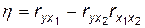(3.29)
Если переменные и не коррелируют с , то 
.Оценивать зависимость с помощью разности (3.29) неудобно. Поэтому ее нормируют так, чтобы получившийся коэффициент был в пределах от – 1 до + 1. В этом случае получаем выражение
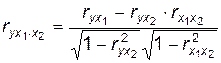. (3.30)
Величина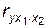 
называется частным коэффициентом корреляции величин и без учета влияния . Если требуется устранить влияние на двух переменных и 
, то по формуле (3.30) вычислим предварительно коэффициенты ,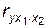 
, 
. Затем вычисляем коэффициент
, (3.31)
который отражает зависимость между и без учета влияния и . Аналогично поступают в случае любого числа переменных. Можно показать, что коэффициент частной корреляции показывает тесноту связи результирующего признака с одним из факторов при неизменном уровне других факторов. Если оценивается теснота связи между и 
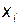без учета влияния 
, то коэффициент частной корреляции может быть рассчитан по формуле:
|
|
, (3.32)
где 
- множественный коэффициент детерминации всех факторов с результатом;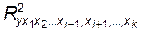 
- множественный коэффициент детерминации модели без i- го фактора.
Наконец, рассмотрим еще один способ расчета частных коэффициентов корреляции, основанный на вычислении корреляционной матрицы выборочных коэффициентов корреляции
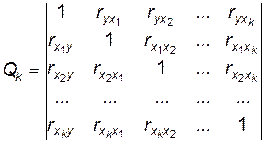. (3.33)
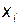Выборочным частным коэффициентом корреляции между и без учета влияния является выражение
= 
,
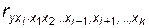где 
, 
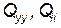— алгебраические дополнения элементов 
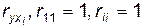матрицы 
.
Частные коэффициенты корреляции имеют те же свойства, что и обычные. При выборе наилучшей модели с их помощью определяют, какая переменная оказывает на переменную выхода наибольшее влияние. Для того чтобы выяснить, существенно ли это влияние, используют различные критерии проверки гипотезы о равенстве нулю некоторых коэффициентов регрессии. Можно, например, воспользоваться 
-критерием, который в данном случае называют частным -критерием. Если изучается влияние переменной 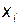входящей в модель с коэффициентом 
, то основная гипотеза имеет вид - 