Возникновения эконометрики

Яновский Л.П., Буховец А.Г.

эконометрика

ОГЛАВЛЕНИЕ

Введение
Глава 1. Сущность и история возникновения эконометрики
1.1. О предмете исследований эконометрики
1.2. Об этапах развития эконометрики
1.3. Контрольные вопросы к главе 1
Глава 2. Парный регрессионный анализ
2.1. Основные понятия регрессионного анализа
2.2. Регрессия по методу МНК
2.3. Предположения и проверка адекватности уравнения регрессии
2.4. Точечный и интервальный прогнозы по уравнению парной регрессии
2.5. Контрольные вопросы и варианты контрольной работы «Парный регрессионный анализ»
2.6. Лабораторная работа № 1 «Модель парной линейной регрессии»
Глава 3. Множественная регрессия
3.1. Постановка задачи
3.2. МНК- модель
3.3. Оценки математического ожидания и ковариаций МНК- коэффициентов модели
3.4. Оценка качества модели
3.5. Доверительные интервалы для коэффициентов регрессии и проверка гипотезы об их значимости
3.6. Доверительный интервал для функции регрессии и для индивидуальных значений зависимой переменной
3.7. Выбор наилучшего набора переменных. Частный коэффициент корреляции
3.8. Процедура шаговой регрессии
3.9. Проблема мультиколлинеарности факторов
3.10. Метод главных компонент
3.11. Линейные регрессионные модели с фиктивными переменными
3.12. Пример использования фиктивной переменной для повышения качества прогнозов при использовании оперативной информации в период уборки урожая
3.13. Тест Г. Чоу для проверки структурных изменений модели
3.14. Выбор модели оптимальной сложности. Тесты Акайка и Шварца
3.15. Контрольные вопросы к главе 3
3.16. Лабораторная работа № 2 «Модель множественной линейной регрессии»
3.17. Лабораторная работа № 3 «Мультиколлинеарность. Отбор наиболее существенных объясняющих переменных в регрессионной модели»
3.18. Лабораторная работа № 4 «Фиктивные переменные во множественной регрессии»
Глава 4. Гетероскедастичность моделей, ее обнаружение и методы устранения гетероскедастичности
4.1 Определение гетероскедастичности модели
4.2. Тестирование гетероскедастичности
4.3. Последствия гетероскедастичности
4.4. Подходы к решению проблемы гетероскедастичности
4.5. Обобщенная линейная модель множественной регрессии. Теорема Айткена и обобщенный метод наименьших квадратов
4.6. Контрольные вопросы к главе 4
Глава 5. Методологические вопросы прогнозирования временных рядов
5.1. Принципы разработки прогнозов
5.2. Анализ и моделирование временных рядов
5.3. Коррелограмма и ее применение
5.4. Выделение тренда в случае нестационарного временного ряда
5.5. Автокорреляция остатков
5.6. Лабораторная работа № 5 «Исследование временного ряда»
5.7. Гармонический анализ временных рядов
5.8. Контрольные вопросы к главе 5
Глава 6. Сглаживание временных рядов
6.1. Линейные фильтры
6.2. Простая скользящая средняя
6.3. Методы взвешенных скользящих средних
6.4. Простое экспоненциальное сглаживание
6.5. Лабораторная работа № 6 “Сглаживание временного ряда
6.6. Элементы диалога в модуле ПП STATISTICA – Анализ временных рядов. Прогнозирование
6.7. Контрольные вопросы к главе 6
6.8. Лабораторная работа № 7 «Сглаживание временных рядов в пакете STATISTICA»
Глава 7. Одновременные уравнения. Методы идентификации
7.1. Уравнения со случайными объясняющими переменными
7.2. Метод инструментальных переменных
7.3. Структурная и приведенная формы системы одновременных уравнений
7.4. Косвенный и двухшаговый метод наименьших квадратов и проблема идентифицируемости
7.5. Контрольные вопросы и упражнения к главе 7.
Глава 8. Моделирование структурными уравнениями
8.1. Обзор основных понятий
8.2. Идеи, лежащие в основе структурного моделирования
8.3. Моделирование структурными уравнениями и диаграммы путей
8.4. Контрольные вопросы к главе 8
Глава 9. Разностные уравнения и их решение
9.1. Уравнения первого и второго порядков
9.2. Системы разностных уравнений более высокого порядка
9.3. Потребление и инвестиции
9.4.Контрольные вопросы к главе 9
Глава 10. Стационарные временные ряды, модели авторегрессии-скользящего среднего
10.1. Основные определения
10.2. Тесты проверки стационарности временного ряда
10.3. Процессы авторегрессии- скользящего среднего
10.4. Условия стационарности для АРСС(p, q) процесса
10.5. Автокорреляционные функции
10.6.Построение АРСС-моделей
10.7. Селекция моделей АРСС
10.8. Алгоритм выбора модели оптимальной сложности для временного ряда в классе АРСС(p, q)-моделей
10.9. Учет сезонности в модели
10.10. Контрольные вопросы к главе 10
ГЛАВА 11. Временные ряды с высокой изменчивостью.
11.1 Авторегрессионые условно - гетероскедастические модели
11.2 Обобщенные авторегрессионые условно гетероскедастические модели (ОАРУГ - модели)
11.3 АРУГ-М модели
11.4 ММП - оценивание ОАРУГ и АРУГ - М моделей
11.5. Контрольные вопросы к главе 11
Глава 12. Ложная регрессия, коинтеграция и модели корректировки ошибок
12.1. Проблема обнаружения ложной корреляции в данных
12.2. Краткосрочные модели, коинтеграция и механизм корректировки ошибок.
12.3 Контрольные вопросы к главе 12
Приложение 1. Элементы линейной алгебры: основные понятия и факты.
Приложение 2. Элементы теории вероятностей и математической статистики: основные понятия и факты.
Приложение 3 Геометрическая интерпретация метода наименьших квадратов
Приложение 4 Критические точки распределения Стьюдента
Приложение 5 Критические точки распределения Фишера
Заключение
Литература
Учебные материалы по эконометрике на английском языке в Интернете

Введение

Государственные стандарты высшего образования включают эконометрику как федеральную компоненту в цикле общих математических и естественнонаучных дисциплин. В настоящее время ощущается нехватка доступных как по цене, так и по содержанию учебных пособий и практикумов по эконометрике. Кроме того, эконометрика опирается на массивы данных и сложных расчетов, поэтому необходимо при преподавании данного курса использовать пакеты вычислительных процедур. В данном пособии авторы используют пакет STATISTICA. На основе этого пакета просчитывались примеры и лабораторные работы настоящего курса. Выбор пакета обусловлен его широким распространением в России, простотой и наглядностью интерфейса, а главное, наличием в продаже ряда пособий по его использованию [4] -[-5].

Пособие состоит из двенадцати глав и лабораторного практикума. В первой главе освещены история возникновения эконометрики и предмет ее исследований. Во второй главе изучается парная регрессия и классические предпосылки использования метода наименьших квадратов (МНК). Множественная регрессия на базе матричного анализа рассматривается в третьей главе. Здесь подробно изучаются вопросы проверки адекватности модели и прогнозирования. Особое внимание уделено случаю мультиколлинеарности объясняющих переменных и моделям с переменной структурой. В четвертой главе изучаются модели с наличием гетероскедастичности в ошибках наблюдений, подходы к решению проблемы гетероскедастичности. Главы пятая и шестая посвящены первичному анализу временных рядов. В пятой главе рассматриваются вопросы выделения линейного и нелинейного тренда, а в шестой главе – адаптивные модели сглаживания временного ряда. В седьмой главе изучаются методы идентификации системы одновременных уравнений на основе косвенного и двухшагового метода наименьших квадратов. Краткий обзор понятий структурного моделирования приведен в восьмой главе. Остальные главы посвящены построению эконометрических моделей временных рядов. В девятой главе изучается вспомогательный материал по теории разностных уравнений. В десятой главе изучаются эконометрические модели Бокса-Дженкинса. В одиннадцатой главе изучаются временные ряды с изменяющейся условной дисперсией. В двенадцатой главе поднимаются вопросы связанные с ложной регрессией, коинтеграцией временных рядов и построение моделей долгосрочной тенденции с коррекцией ошибок.

Лабораторный практикум состоит из семи лабораторных работ отражающих содержание основных глав пособия.

Изложение материала сопровождается контрольными вопросами, примерами, задачами. Предлагается тематика контрольных работ по узловым моментам курса. В отличие от имеющихся пособий авторы не приводят развернутые математико-статистические таблицы в приложениях, так как предполагается использование для этих целей возможностей статистических пакетов.

Глава 1

 

Сущность и история

возникновения эконометрики

1.1. О предмете исследований эконометрики

Курс эконометрики занимает важное место в современных программах экономических вузов во всем мире наряду с такими предметами как микроэкономика, макроэкономика, финансовый анализ. Эконометрические методы являются инструментом для прогнозирования в банковском деле, финансах, бизнесе, при государственном регулировании экономики. Что же такое эконометрика? Эконометрика — быстроразвивающаяся отрасль экономической науки, цель которой состоит в количественном описании экономических отношений. Приведем несколько цитат о существе данной науки.

«Эконометрика позволяет проводить количественный анализ реальных экономических явлений, основываясь на современном развитии теории и наблюдениях, связанных с методами получения выводов» (Самуэльсон).

«Основная задача эконометрики – наполнить эмпирическим содержанием априорные экономические рассуждения» (Клейн).

«Цель эконометрики — эмпирический анализ экономических законов. Эконометрика дополняет теорию, используя реальные данные для проверки и уточнения постулируемых отношений» (Маленво).

Термин «эконометрия» был впервые введен П. Цьемпой в 1910 году, который пытался применить методы алгебры и геометрии к анализу хозяйственной деятельности. В настоящее время этот термин используется для того раздела эконометрики и теории экономического анализа, который изучает влияние факторов, формирующих результаты работы фирмы (предприятия)[1].

В мировой науке общеупотребимым стал термин «эконометрика» для науки об измерении и анализе экономических явлений. Эта наука возникла на стыке трех дисциплин: экономической теории, методов математического анализа и математической статистики, несколько позднее - программирования и вычислительной техники. Основатель журнала «Эконометрика» Р. Фриш (1895–1973) привел следующее определение эконометрики: «Эконометрика — это не то же самое, что экономическая статистика. Она не идентична тому, что мы называем экономической теорией, хотя значительная часть этой теории носит количественный характер. Эконометрика не является синонимом приложений математики к экономике. Как показывает опыт, каждая из трех отправных точек — статистика, экономическая теория и математика — необходимое, но не достаточное условие для понимания количественных соотношений в современной экономической жизни. Это — единство всех трех составляющих. И это единство образует эконометрику» [2].

Пока еще рано утверждать, что достигнуто однозначное определение эконометрики. Есть, по крайней мере, еще четыре дисциплины использующие в своей основе математические методы в применении к экономике: многомерный статистический анализ данных (тесно связанный с эконометрикой)[3]; финансовая математика, также использующая в современных своих разделах эконометрические методы[4]; математические модели в экономике — наука, применяющая для подтверждения теоретических концепций эконометрическую технику верификации моделей[5]; математические методы в экономике (старое название — исследование операций) — наука о постановках и решении оптимизационных задач в экономике, состоящей из таких широко известных разделов как линейное и нелинейное программирование, сетевое планирование, управление запасами, теория игр. Несколько особняком стоит теория массового обслуживания.

Некоторые исследователи, например, Э. Маленво придавали широкое толкование эконометрике, интерпретируя ее как «любое применение математики или статистических методов к изучению экономических явлений»[6]. Однако доминирующим стало мнение, что эконометрика применяет статистические подходы к эконометрическим измерениям. Это обстоятельство обусловило содержание настоящего курса лекций.

В свою очередь эконометрика содержит два больших раздела: моделирование данных неупорядоченных во времени и теорию временных рядов.

1.2. Об этапах развития эконометрики

Эконометрика прошла длинный путь зарождения и выделения в самостоятельную область знания. Одним из первых количественных законов был «закон Кинга» (Г. Кинг (1648–1712)), в котором выяснялись закономерности спроса на основе соотношений между урожаем зерновых и ценами на зерно. Первые применения парной корреляции появились на рубеже 19-го и 20-го веков (Дж. Э. Юл, 1895, 1896, Г.Хукер, 1901), в которых изучались показатели благосостояния.

С 30-х годов 19-го века страны с высоким уровнем развития капитализма стали сотрясать кризисы производства, которые неоклассическая теория спроса и предложения не могла объяснить. Марксистская экономическая теория в ее классическом варианте также была удалена от конкретной практики хозяйствования. Для практических приложений требовались количественные выражения базовых понятий теории, таких как производственная функция, эластичность спроса, предельная полезность и др.

Первой книгой, которую можно назвать эконометрической, была книга американского ученого Г. Мура «Законы заработной платы: эссе по статистической экономике» (1911). В ней дана практическая проверка теории производительности Дж. Кларка, а также излагались основы стратегии тред-юнионов на основе достижений теории корреляции, регрессии, анализа динамических рядов. В это же время в Италии Р. Бенини (1862–1956) применял метод множественной регрессии для оценки функции спроса.

Значительный вклад в становление эконометрики внесли ученые занимавшиеся проблемой цикличности в экономике, такие как К. Жюгляр, К. Маркс, С. Китчин, С. Кузнец, Н. Кондратьев. Они выявили цикличность инвестиций в активную часть основных фондов (7–11 лет), цикличность обновления оборотных средств (3–5 лет), циклы в строительстве (15–20 лет), долгосрочные циклы обновления инфраструктуры (пассивной части основных фондов) Кондратьева (40–60 лет).

Для построения эконометрических моделей использовался метод К. Гаусса. В этой связи напомним, что по оценке К. Гаусса, метод наименьших квадратов он разрабатывал в противовес методу, предложенному в 1755 году Р. Босковичем, а в 1789 году, уточненному П. Лапласом, которые ориентировались изначально на минимизацию суммы модулей отклонений расчетных значений от фактических. Предложение Гаусса исходило из предположения, что в случае перехода к поиску минимума по сумме квадратов появляется возможность существенно упростить решение на основе дифференциального исчисления.

Среди эконометрических исследований 40-х годов выполненных в России отметим работы В.М. Обухова[7]. Это был первый ученый, которому удалось за довольно продолжительный период времени (1872–1931 гг.) на союзном уровне описать динамику урожайности зерновых культур уравнениями с малым числом параметров. Здесь для нас особенно примечателен тот факт, что методы выполнения прогностических работ, использованные В.М. Обуховым, задолго до современных авторов уже предполагали разбиение изучаемой совокупности на «обучающую» и «проверочную» части (cross-validation method).

Новым этапом в формировании эконометрики явилось построение экономических предсказателей (барометров), в частности гарвардского барометра. Идея заключалась в предсказании динамики одних элементов экономики с помощью других, которые в своих изменениях опережают первые. В течение 1903–1914 годов и нескольких лет после первой мировой войны удавалось прогнозировать поворотные пункты в усредненных кривых фондового рынка, товарного рынка и денежного рынка с заблаговременностью несколько месяцев. Но со второй четверти 20-го века гарвардский барометр потерял прогнозирующие свойства возможно в связи с появлением мощных внешних регулирующих воздействий на экономику США.

Вообще к подтверждению существования статистических зависимостей надо подходить с особой осторожностью. Так известный советский статистик-математик Е. Слуцкий (1880–1948) в работе 1927 года взял в качестве случайных рядов последние цифры номеров облигаций из тиражных таблиц выигрышного займа и показал, что «сложение случайных причин порождает волнообразные ряды, имеющие тенденцию на протяжении большего или меньшего числа волн имитировать гармонические ряды, сложенные из небольшого числа синусоид». В настоящее время существуют теоретические подходы к проверке надежности прогнозов[8]. Возможно также проявление законов самоорганизации при сложении случайных величин. Например, если складывать большое число однородных случайных слагаемых, то в результате получается случайная величина, подчиняющаяся нормальному закону распределения.

Оказывается, что при усреднении большого числа разновеликих слагаемых возникают естественным путем самоподобные процессы. Так распределение дневных колебаний курса доллара будет напоминать распределение недельных колебаний курса, но, конечно, с другими числовыми характеристиками среднего, дисперсии и т.д.

В 30-е годы были перен­есены в экономические исследования из астрономии, физики методы спектрального анализа временных рядов. После исключения тенденции (тренда) кривая временного ряда приближенно описывалась в виде волнообразной кривой, в свою очередь составленной из суммы небольшого числа гармоник, то есть функций вида y = A₁ + A₂sin(kt + e). Возможна аппроксимация гармониками и без предварительного выделения тенденции (тренда). Это направление получило значительное развитие в последнее время: развита теория волновых пакетов для нестационарных временных рядов (wavelet theory).

В конце 1930 года в США было создано первое международное эконометрическое общество. С 1933 года стал издаваться журнал «Econometrica». В 1941 году появился первый учебник по эконометрике, автором которого был Я. Тинберген (1913–1994).

До 70-х годов эконометрика рассматривалась в качестве инструмента подтверждения на эмпирических наблюдениях количественных соотношений разработанных в теории. Это объяснялось тем, что эконометрические модели, разрабатываемые в тот период, были всегда кейнсианскими. Позднее, когда началась ожесточенная дискуссия среди кейнсианцев, монетаристов и последователей других экономических теорий, формальные методы эконометрики стали использоваться для доказательства выбора тех или иных теоретических концепций.

Схематически применение эконометрики до 70-х годов и после 70-х можно представить на двух рисунках (см. рис. 1 и рис. 2).

В эти же годы бурное развитие вычислительной техники стало толчком для развития трудоемких с вычислительной точки зрения методов анализа временных рядов. Г. Бокс и Г. Дженкинс создали теорию интегрированных моделей авторегрессии — скользящего среднего (ARIMA). Широкое распространение получает альтернативный методу наименьших квадратов метод максимального правдоподобия, сводящийся к решению систем нелинейных уравнений.

В начале 80-х годов развиваются методы решения систем одновременных уравнений (VAR модели), путевой анализ. Для решения систем одновременных уравнений используются косвенный, двухшаговый и трехшаговый методы наименьших квадратов, метод максимального правдоподобия.

Следует разъяснить, в чем состоит тестирование конкурирующих экономических гипотез. Во-первых, величина и знак коэффициентов моделей должны согласовываться с теорией. Во-вторых, среди конкурирующих гипотез следует отдать предпочтение той гипотезе, у которой эконометрическая модель обладает лучшими прогнозирующими свойствами. Испытания надо проводить обязательно на тех данных, которые не использовались при построении модели (независимом материале).

 

 

Рис. 1. Схематическое описание последовательных этапов эконометрического анализа экономических теоретических моделей до 70-х годов

 

В самом начале 90-х годов была создана теория коинтеграции временных рядов и на ее основе модели исправления ошибки (error correction model) включающие краткосрочные изменения, которые поддерживают долгосрочное равновесие. Двухстадийный процесс построения модели Ингла-Грейнджера (1987) включал на первом этапе оценку регрессии, описывающей коинтеграцию временных рядов, а на втором этапе – построение модели исправления ошибки. В многомерном случае, когда может существовать более одного вектора коинтеграции, нужно было разработать методологию определения структуры всех векторов коинтеграции. Такая техника была предложена Йохансеном в 1988–1990 годах.

В связи с нарастающей неустойчивостью финансовых рынков возрастал интерес к изучению нестационарности финансовых рисков. Мандельброт в 60-х годах обнаружил в рядах активов наличие «долговременной памяти», выражавшейся в том, что большие изменения цен активов влекут за собой большие изменения в сторону, как возрастания, так и убывания, в то время как малые изменения влекут малые изменения. В частности, финансовые переменные имеют спокойные периоды, за которыми следуют периоды сравнительной нестабильности. То есть нестабильность (волатильность) является не постоянной, а изменяющейся во времени. В 80-х начале 90-х годов Ингл (Engle, 1982), а затем Боллеслев (Bolleslev, 1986) и Нельсон (Nelson, 1991) разработали эконометрические модели предсказания будущей нестабильности (модели авторегрессионой условной гетероскедастичности (ARCH-модель) и модели обобщенной авторегрессионой условной гетероскедастичности (GARCH-модель)).

 

 

Рис. 2. Схематическое описание последовательных этапов эконометрического

анализа экономических теоретических моделей в настоящее время

 

Эконометрика в настоящее время завоевала всеобщее признание. Четыре нобелевские премии по экономике были присуждены за вклад в развитие эконометрической науки. Премия 1969 года была присуждена Р. Фришу и Я. Тинбергену, стоявшим у истоков зарождения эконометрики как науки. Премия 1980 года — Л. Клейну за применение эконометрических моделей к анализу экономических колебаний и в экономической политике. Премия 1989 года — Т. Хаавельмо за разработку и анализ одновременных (структурных) экономических уравнений. Премия 2000-го года Дж. Хекману — за развитие теории селективных выборок и Д. Макфаддену за развитие моделей дискретного выбора. Премия 2003 года Инглу и Грейнджеру за создание моделей условной регрессионной гетероскедастичности и развитие теории коинтеграции временных рядов.

На современном этапе развития эконометрическое исследование может включать несколько из ниже перечисленных проблем:

1) при исследовании моделей по независимым неупорядоченным наблюдениям:

· выделение зависимых и независимых переменных согласно некоторой экономической гипотезе;

· подбор и анализ данных, преобразование данных в удобном для эконометрического исследования виде;

· выбор формы связи между зависимыми и независимыми переменными, спецификация модели, выбор наилучшего подмножества объясняющих переменных;

· оценка параметров модели;

· проверка ряда гипотез о виде распределения или о числовых характеристиках случайной компоненты уравнения;

· анализ статистической значимости мультиколлинеарности в объясняющих переменных (предикторах);

· необходимость использования фиктивных переменных в случае неоднородности данных;

· выявление автокорреляции в остатках и пересчет коэффициентов модели при наличии автокорреляции;

· селекция и отбор наиболее конкурентоспособных моделей на независимом материале, проверка адекватности моделей;

· анализ структуры связей и построение системы одновременных уравнений, путевой анализ;

· проверка условия идентификации системы одновременных уравнений;

· оценивание параметров системы одновременных уравнений;

· прогноз и применение к экономической политике результатов моделирования;

2) при исследовании моделей временных рядов:

· выявление тренда, лагов, циклической компоненты;

· проверка остатков на гетероскедастичность;

· анализ внутренней структуры рядов, анализ специфики убывания автокорреляций и взаимных корреляций, наличие «долговременной памяти», расчет фрактальной размерности и т.д.;

· анализ структурных изменений ряда, определение переломных моментов в ряду (break point);

· построение сглаженных временных рядов, рекурсивных, адаптивных моделей;

· построение ARIMA и VAR — моделей;

· идентификация и оценивание параметров моделей (в условиях неприменимости метода наименьших квадратов);

· проблемы выявления стационарности и коинтеграции, построение и оценка параметров моделей с исправлением ошибок;

· Прогноз и применение к экономической политике результатов моделирования.

1.3. Контрольные вопросы к главе 1«Сущность и история возникновения эконометрики»

1. Приведите высказывания различных ученых о сущности эконометрики. Попытайтесь сформулировать определение эконометрики как науки на основе этих высказываний.

2. Расскажите об истории возникновения эконометрики. Кто и когда написал первый учебник по эконометрике? Какие учебники по эконометрике Вам рекомендованы для изучения курса?

3. Какова была схема эконометрических исследований до и после 70-х годов 20-го века?

4. Какие новейшие исследования были проведены в 80–90-х годах 20–го века?

5. Сформулируйте задачи эконометрического исследования на современном этапе развития.

Глава 2

 

Парный регрессионный

Анализ

Основные понятия регрессионного анализа

Регрессионный анализ является одним из наиболее распространенных инструментов эконометрического анализа. Регрессионный анализ анализирует и оценивает связи между зависимой (объясняемой) переменной и независимыми (объясняющими) переменными. Зависимую переменную иногда называют результативным признаком, а объясняющие переменные – предикторами, регрессорами или факторами. Как это часто бывает, название метода не связано с его существом, а имеет исторические корни. Термин регрессия ввел лорд Френсис Гальтон (1822–1911), исследуя связь между ростом родителей и детей. Он установил, что хотя у высоких родителей — высокие дети, а у маленьких чаще рождаются маленькие дети, рост у детей имеет тенденцию постепенно стремиться к средним значениям, выравниваться. Гальтон, будучи аристократом, к такой тенденции относился негативно и назвал ее регрессией (упадком).

Обозначим зависимую переменную за y, а независимые (объясняющие) переменные за x₁, x₂, …, x_k. Если k = 1, и есть только одна независимая переменная x₁ (которую обозначим x), то регрессия называется простой (simple) или парной. Если k = 2, 3, …, то регрессия называется множественной.

Сейчас мы обсудим вопросы, связанные с априорными предположениями, оценкой коэффициентов и доверительными интервалами для прогноза парной регрессии.

Начнем с построения простейшей модели

 

Y = a + bx + e, (2.1)

 

где Y — зависимая переменная, состоящая из двух слагаемых: 1) неслучайной составляющей Y1 = a + bx (x – независимая переменная, a и b - постоянные числа — параметры уравнения); 2)случайного члена e. Пусть имеется таблица данных (рис. 1). На графике эти данные можно представить в виде табл. 2.1 и рис. 2.1.

Предположим, что истинная зависимость между x и y – линейная, то есть существует некоторая прямая Y1 = a + bx, отражающая «истинную» зависимость. Задача регрессионного анализа состоит в получении оценок a, b и, следовательно, в определении положения прямой по точкам. На рис. 2.2 такое уравнение построено с использованием возможности графики в пакете «STATISTICA».

 

 

Таблица 2.1

 

Рис. 2.1

 

Рис. 2.2

 

Почему существуют отклонения от прямой регрессии, то есть случайные слагаемые e? Для этого есть несколько причин:

1. Ошибки измерения. Например, при сборе данных об урожайности сельскохозяйственных культур, результаты работы в отчетах могут завышаться или занижаться в зависимости от экономической политики, данные оценивались «на глазок» и т.д.

2. Невключение объясняющих переменных. Возможно, что простая зависимость Y = a + bx является очень большим упрощением. Наверняка существуют и другие факторы, влияющие на изменение Y, и которые не удалось оценить и включить в уравнение.

3. Неправильный выбор вида зависимости в уравнении. Возможно зависимость не линейная, а более сложная. Приведем наиболее употребительные виды связей, использующихся при построении парной регрессии:

 

Y = a + b/x; Y = ax^b; Y = ab^x; Y = a + bx + cx²; Y = a + bx + cx² + dx³;

Y = 1/(a + bx); Y = a + bx + c/x; Y = 1/(a + bx + cx²); Y = a + b × tgx;

ln Y= a + bx; Y = a/(1 + be^-cx) и др.

 

Вид зависимости выбирают либо графически, либо проверяя качество моделей на контрольной выборке, либо используя априорные экономические соображения. Например, валовой выпуск продукции Y в зависимости от числа x занятых работников в производстве может быть описан уравнением Y = ax^b, где 0 < b < 1. Разделив уравнение слева и справа на x получим зависимость производительности труда от числа работников в производстве: Пр Y = a/x^1-b = a/x^c 0 < c < 1.

4. Уравнение регрессии отражает связи между агрегированными переменными. Так, например, зависимость между урожайностью и количеством внесенных удобрений индивидуальна для различных полей и любая попытка определить зависимость между совокупным урожаем и совокупным внесением удобрений является лишь приближением, аппроксимацией.

Для оценивания параметров a, b обычно применяют метод наименьших квадратов (МНК). Существуют и другие методы оценки параметров, такие как: метод моментов, метод наименьших модулей, метод максимального правдоподобия.

 

Регрессия по методу МНК

Пусть имеется n наблюдений и, следовательно, уравнение (2.1) можно переписать в виде:

 

Y_i = a + bx_i +e_i, i = 1, 2, 3 … n (2.1)

 

Случайное слагаемое e можно рассматривать как последовательность n случайных величин e_i, i = 1, 2, 3 … n.

Метод наименьших квадратов состоит в том, чтобы получить такие оценки a и b параметров a и b, при которых сумма квадратов отклонений e фактических значений признака Y_i от расчетных (теоретических) 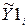[9] была бы минимальна:

 

(2.2)

 

Найдем минимум функции 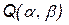, приравняв производные по каждой переменной нулю. Имеем

 

(2.3)

 

После преобразований получаем систему уравнений:

 

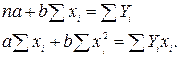(2.4)

 

Система уравнений (2.4) называется системой нормальных уравнений МНК.

Находим a и b, решая систему (2.4):

 

, (2.5)

 

где ,

, .

 

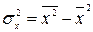Коэффициент b при x называется выборочным коэффициентом регрессии. Если переменную x изменить на единицу, то есть взять за x величину x + 1, то новое значение Y1(x + 1 ) будет равно Y1(x) + b. Следовательно, коэффициент регрессии показывает среднее изменение результата Y при изменении фактора x на единицу.

Коэффициент a указывает на значение результирующего признака при нулевом значении фактора. Этот факт является важным индикатором для выбора вида уравнения регрессии. Например, если в результате вычислений коэффициент a оказался отрицательным, а экономический смысл задачи диктует положительность или равенство нулю показателя a, значит выбор вида уравнения, был неудачен.

Произведем расчеты для данных представленных в табл. 2.1.

Итак, систему уравнений (2.4) для данных табл. 2.2 перепишем в виде

 

.

 

Таблица 2.2

 

Решая последнюю систему, получаем a = 0,924; b = 0,658. Построим таблицу, содержащую исходные данные, расчетные значения 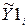= 0,924 + 0,658 x_i и остатки = Y_i - 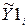= Y_i - 0,924 - 0,658 x_i.

 

Таблица 2.3