1) Для определения типа процесса построим его коррелограмму по формулам (5.8)-(5.12). Коррелограмму будем строить по четырем точкам (n = 15, l £ n/ 4 » 4 ) r1, r2, r3, r4. Получаем, после вычислений
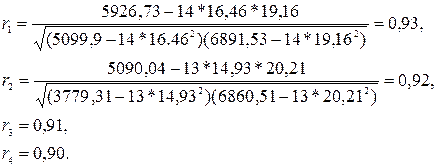
По результатам вычислений получаем коррелограмму (рис. 5.5).
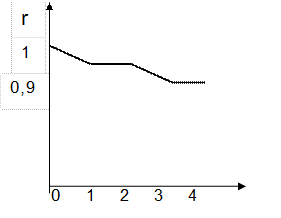Очевидно, что это коррелограмма нестационарного временного ряда (см. рис 5.1б). Поэтому, можно предположить, что у этого ряда имеется тренд среднего уровня (имеется тренд у математического ожидания ряда).
2) Оценим форму кривой тренда. Для этого по форме корреляционного поля (см. рис. 5.6) подберем соответствующие кривые и для них вычислим последовательные разности.
По виду корреляционного поля подходят (см. табл. 5.1) две зависимости:
X1(t) = a + bt (b > 0),
X1(t) = aexp (bt) (b > 0).
Сравним эти зависимости, используя критерий из табл. 5.1. Найдем 
Рис. 5. 6
Для прямой имеем
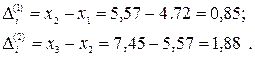
и так далее.
Получаем, в результате
D(1) = { 0,85;1,88;1,14;0,93;1,13;1,99;2,49;1,9;3,41;2.57;4,49;4,20;4,67;6,25 }.
Для экспоненты X2(t), имеем
Di(1) = lnxi+1 – lnxi; Di(1) =ln5,57 – ln4,72=0,17
и так далее.
В результате
D(1)={ 0,17;0,29;0,14;0,10;0,11;0,17;0,18;0,12;0,18;0,12;0,18;0,14;0,16 }.
Очевидно, для экспоненциальной зависимости равенство Di(1) = const более приемлемо, чем для линейной зависимости. Оценим параметры a и b, решив систему нормальных уравнений МНК:
Вычисляем необходимые суммы
 |
Получаем систему
.
Тогда, lna = 1,47; a = exp(lna) = 4,35; b = 0,15.
Получим модель тренда X = 4.35 *exp( 0,15t ).
Для сравнения приведем график выравнивания данного ряда с помощью экспоненциальной модели из пакета «STATISTICA»(см. рис.5.7). Некоторые расхождения в оценке коэффициентов объясняются погрешностями наших вычислений.
3). Проверим правильность полученной модели на основе поведения ряда остатков. Обозначим e(t) = X(t) - 4.35 *exp( 0,15 t). Тогда
|
|
e(t1) = 4,72 – 4.35 *exp( 0,15*1 ) = – 0.35;
e(t2) = 5,57 – 4.35 *exp( 0,15*2 ) = – 0,34.
Аналогично получаем остальные e(ti), i = 3, 4, …, 15. В результате имеем ряд остатков:
e(ti) ={–0,35; –0,34; 0,56; 0,56; 0,17; –0,23; –0,04; 0,35; –0,18; 0,38; –0,37; 0,26; –0,05; –0,67; –0,54 }.
Рис. 5.7
Проверку соответствия найденной модели тренда можно осуществить тремя путями. Во-первых, проверим случайность ряда остатков на основе критерия поворотных точек (см. формулу (5.15)). Находим, что поворотных точек в нашем ряду восемь
(0,56; –0,23; 0,35; –0,18; 0,38; –0,37; 0,26; –0,67).
Вычислим правую часть q неравенства (15) при n = 15:
Так как p = 8 > q = 5, и p = 8 существенно меньше n – 2 = 13, то ряд остатков по данномукритерию можно считать случайным.
Во-вторых, если модель тренда адекватна ряду, то ряд из остатков должен быть стационарен. Выпишем для ряда e(ti) коэффициенты автокорреляции. Получим, что
r1 (e) = 0,14; r2 (e) = – 0,19; r3 (e) = – 0,23; r4 (e) = 0,12.
Колебания rk (e); k = 1, 2, 3, 4 по знаку и небольшие (незначимые) значения rk(e) по абсолютной величине означают стационарность ряда остатков.
В третьих, проверим отсутствие автокорреляции остатков по критерию Неймана Q = F/S2.
Итак, Q = 0,246/0,147 = 1,65.
По табл.5.2 находим для уровня значимости a = 0.05 и n = 15 критическое значение Qкр = 1,29.
Так как Q > Qкр, то можно принять гипотезу об отсутствии автокорреляции остатков.
Аналогичные расчеты можно провести, используя пакеты STATISTICA или STATGRAPHICS, например, используя модель
X = 4.354 *exp (0,153 t),
найденную выше (см. рис. 5.7), получаем таблицу значений остатков (см. табл. 5.4, переменная RESIDUAL).
|
|
Вычислим для этого ряда остатков автокорреляции. Последний столбец P показывает вероятности того, что найденные автокорреляции равны нулю. Высокие значения P означают, что полученные автокорреляции статистически незначимы.
Рис. 5.8. Автокорреляционная функция процесса.
Предпоследний столбец Q дает статистику Бокса- Льюиса. Небольшие значения Q указывают на адекватность построенной модели временного ряда. Вычислим для ряда остатков статистику Дарбина –Ватсона. Она оказывается равной 2,1145. Близость к числу 2 статистики DW свидетельствует об удачном выборе модели.
Таблица 5.4
| № | Данные | Расчетные данные | Остатки |
| 4,720 | 5,074 | -,354 | |
| 5,570 | 5,913 | -,343 | |
| 7,450 | 6,890 | ,560 | |
| 8,590 | 8,029 | ,561 | |
| 9,520 | 9,357 | ,163 | |
| 10,660 | 10,904 | -,244 | |
| 12,650 | 12,706 | -,056 | |
| 15,140 | 14,807 | ,333 | |
| 17,050 | 17,255 | ,205 | |
| 20,460 | 20,108 | ,352 | |
| 23,030 | 23,432 | -,402 | |
| 27,520 | 27,306 | ,214 | |
| 31,720 | 31,820 | -,100 | |
| 36,340 | 37,081 | -,741 | |
| 42,590 | 43,211 | -,621 |
Можно было бы использовать при выборе тренда более сложную модель вида X(t) = c + exp(b0 + b1t) (см. таблицу 5.1, последняя модель). Вручную расчеты для этой модели выполнять затруднительно. Представим на рис.5.9 результаты расчетов с помощью пакета STATISTICA, раздел «Нелинейное оценивание».
Рис. 5.9
Оценивая полученную модель визуально, убеждаемся в ее адекватности. Однако, как показывает опыт, если получены две адекватные модели временного ряда, то лучше использовать для прогноза более простую модель.
Варианты заданий к лабораторной работе № 5
|
|