Предположим, что в регрессионной модели (3.1)
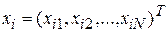- столбец, состоящий из значений 
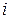- той случайной переменной в 
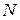наблюдениях, а 
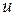- номер наблюдения 
, 
-теоретические значения коэффициентов модели, 
- ошибка в 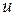- том наблюдении,
Ранее считалось, что значения объясняющих переменных 
постоянные, то есть не изменились бы, если провести новую серию из 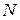экспериментов. Изменились бы при этом повторении случайные ошибки и, следовательно, результирующая переменная 
.
Необходимость рассмотрения уравнений со случайными объясняющими переменными вызвана тем, что при исследовании временных рядов многие объясняющие переменные сами представляют временной ряд и предполагать их полную предсказуемость (детерминированность) было бы неверно.
Вопрос о применимости обычного МНК, в этом случае, тесно связан с наличием или отсутствием корреляции между объясняющими переменными и случайными ошибками . Если корреляция отсутствует, то применение МНК дает несмещенные и состоятельные оценки коэффициентов регрессии . Доказательство этого факта является простым обобщением соответствующего доказательства для детерминированного случая. Однако, если объясняющие переменные коррелирует с ошибками регрессии в прошлых наблюдениях, то доказательство состоятельности оценок коэффициентов становится неверным. Если, более того, объясняющие переменные коррелирует с ошибками регрессии в текущих наблюдениях, то нарушается и свойство несмещенности оценок МНК.
Существует ряд причин, которые в экономических моделях влекут зависимость между объясняющими переменными и случайными ошибками . Например, существует некоторый фактор, который одновременно влияет на поведение случайной ошибки и объясняющей переменной.
|
|
Приведем следующий пример. Предположим, что строится линейная модель прогноза будущих розничных цен на некоторый сельскохозяйственный продукт после переработки, например, на подсолнечное масло. При этом, в качестве единственной объясняющей переменной принимается средняя оптовая закупочная цена на семена подсолнечника. Очевидно, урожайность подсолнечника является случайной величиной, изменяющейся от года к году, и влияющей одновременно на оптовую закупочную цену семян подсолнечника и на отклонение фактической розничной цены в данном году от расчетной модельной розничной цены, учитывающей только размер закупочных цен. Данное отклонение отражает неучтенные факторы рынка, такие как повышенный спрос в связи с неурожаем или незначительное снижение или даже рост розничных цен на монопольном рынке при хорошем урожае подсолнечника. При среднем урожае закупочные цены будут средними и ошибка модели минимальна, при плохом и хорошем урожае будут изменяться как закупочные цены, так и возрастать ошибки модели.
Вторым обстоятельством, вызывающим корреляцию между факторами и ошибками уравнения регрессии часто являются ошибки при измерении объясняющих переменных. В модель подставляются не истинные, а искаженные наблюдения. Ошибка наблюдения в модели теперь будет состоять из двух слагаемых: ошибок регрессии и ошибок при расчете факторов. Отсюда следует коррелированность факторов и ошибок модели, тем большая, чем больше дисперсия ошибок расчета факторов.
Для устранения возникающих трудностей построения уравнения регрессии при наличии коррелированности факторов и ошибок модели используют метод инструментальных переменных.
|
|