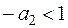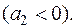9.1. Уравнения первого и второго порядков
Пусть дана функция  . Тогда первая разность
. Тогда первая разность 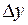 определяется формулой
определяется формулой
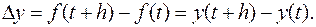 (9.1)
(9.1)
В отличие от дифференциального исчисления мы не предполагаем, что h стремится к нулю. Так как большинство экономических данных собираются через определенные равные промежутки времени, полезно считать, что  . Более того, обычно полагают период между наблюдениями
. Более того, обычно полагают период между наблюдениями 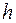 нормализованным, то есть выбирают
нормализованным, то есть выбирают  (1 месяц, 1 квартал, 1 год). Поэтому мы можем записать первые разности в виде
(1 месяц, 1 квартал, 1 год). Поэтому мы можем записать первые разности в виде
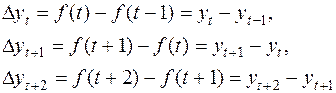
и т.д.
Тем же путем мы сформируем вторую разность как изменение первой разности. Рассмотрим

Аналогично определяется разность 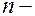 ого порядка:
ого порядка:

Так как в настоящей книге в основном рассматриваются линейные модели временных рядов, мы изучим только один специальный случай линейного разностного уравнения n-ого порядка с постоянными коэффициентами, а именно, уравнение вида
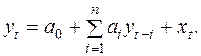 (9.2)
(9.2)
Порядок разностного уравнения задается показателем n (максимальной величиной шага запаздывания или, другими словами, максимальным лагом). Уравнение считается линейным потому, что все значения зависимой переменной y входят в него в первой степени.
Коэффициенты 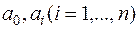 называются параметрами уравнения (1.2) и не зависят от значений x и y. Переменная x представляет возмущающий процесс и может зависеть от времени, текущего и прошлого значений других переменных или иметь стохастический характер изменения. Соответственно выбирая возмущающий процесс x, можно получить широкий спектр важных макроэкономических моделей.
называются параметрами уравнения (1.2) и не зависят от значений x и y. Переменная x представляет возмущающий процесс и может зависеть от времени, текущего и прошлого значений других переменных или иметь стохастический характер изменения. Соответственно выбирая возмущающий процесс x, можно получить широкий спектр важных макроэкономических моделей.
Рассмотрим, например, стохастическую версию классической модели Самуэльсона (1939 г.):
 (9.3)
(9.3)
где 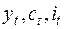 означают соответственно реальный общий национальный продукт (real GNP), потребление и инвестиции в момент времени t. Слагаемые
означают соответственно реальный общий национальный продукт (real GNP), потребление и инвестиции в момент времени t. Слагаемые 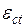 и
и 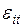 имеют нулевые средние и объясняют случайные возмущения в потреблении и инвестировании.
имеют нулевые средние и объясняют случайные возмущения в потреблении и инвестировании.
Преобразуем кейнсианскую модель (9.3) производства и потребления к виду
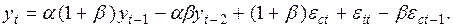 (9.4)
(9.4)
Уравнение (9.4) выражает теперь 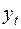 как функцию от собственных запаздываний (лагов) и возмущающих членов. Выберем возмущающий процесс в виде
как функцию от собственных запаздываний (лагов) и возмущающих членов. Выберем возмущающий процесс в виде
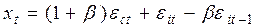 .
.
и получим разностное линейное уравнение второго порядка вида (9.2). Отметим, что в уравнении (9.4) отсутствует свободный член, то есть 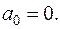
Важный частный случай для последовательности  мы получаем при
мы получаем при 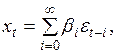 где
где  – константы, а
– константы, а  не зависят от y. При этом можно полагать, что
не зависят от y. При этом можно полагать, что 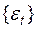 является последовательностью неопределенных внешних (экзогенных) переменных. Например, если
является последовательностью неопределенных внешних (экзогенных) переменных. Например, если 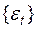 – последовательность случайных ошибок наблюдений и положить
– последовательность случайных ошибок наблюдений и положить  , то уравнение (9.2) становится уравнением авторегрессии:
, то уравнение (9.2) становится уравнением авторегрессии:

Пусть 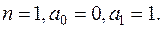 Тогда мы получаем модель случайного блуждания (random walk model), которая широко используется в дальнейшем.
Тогда мы получаем модель случайного блуждания (random walk model), которая широко используется в дальнейшем.
Другой полезный пример дает уравнение
 . (9.5)
. (9.5)
Можно проверить, что решением этого разностного уравнения первого порядка является функция
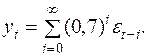 (9.6)
(9.6)
Перейдем к методам решения разностных уравнений.
Метод итераций (последовательных приближений).
Обозначим известное значение функции y в момент времени 0 за y0. Рассмотрим разностное уравнение первого порядка
 (9.7)
(9.7)
Подставляя y0 в (9.7), получаем
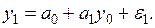
Тем же путем находим
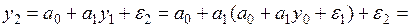

Продолжая процесс, найдем y3

Для итерации с номером t получаем решение уравнения (9.7):
 . (9.8)
. (9.8)
Предположим теперь, что начальное значение y0 не известно. Тогда при движении “назад” заменим y0 на итерацию “назад” 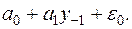 В результате получаем
В результате получаем
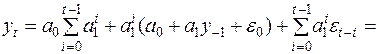
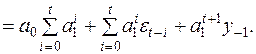
Предполагая, что  и сдвигаясь назад на m периодов (
и сдвигаясь назад на m периодов ( ), получаем
), получаем 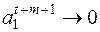 и
и  Тогда
Тогда 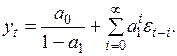
Можно показать, что полученное решение уравнения (9.7) не единственное. Решением уравнения (9.7) будет при любом С и выражение
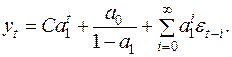 (9.9)
(9.9)
Выражение (9.9) как и в случае дифференциальных уравнений первого порядка представляет сумму общего решения 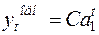 однородного разностного уравнения вида (9.2)
однородного разностного уравнения вида (9.2) 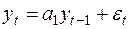 и частного решения неоднородного уравнения (9.7).
и частного решения неоднородного уравнения (9.7).
Рассмотрим теперь случай 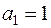 . Тогда движением “назад” получаем решение в виде:
. Тогда движением “назад” получаем решение в виде:  В отличие от предыдущего случая теперь ошибки
В отличие от предыдущего случая теперь ошибки  не убывают, а накапливаются.
не убывают, а накапливаются.
Рассмотрим теперь уравнение второго порядка
 . (9.10)
. (9.10)
Будем искать решение уравнения 2-го порядка в том же виде:
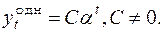
Подставляя это выражение в (9.10), получаем
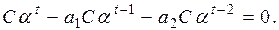 (9.11)
(9.11)
Разделив обе части (9.11) на 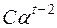 , получим характеристическое уравнение
, получим характеристическое уравнение  При решении характеристического уравнения могут возникнуть три случая.
При решении характеристического уравнения могут возникнуть три случая.
1. Дискриминант  и существуют два действительных различных корня уравнения. Тогда
и существуют два действительных различных корня уравнения. Тогда

Если абсолютное значение хотя бы одного из корней 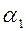 или
или 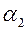 превышает единицу, то однородное решение имеет “взрывной” характер при
превышает единицу, то однородное решение имеет “взрывной” характер при 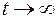 .
.
2. Если  , то общее решение получается в виде:
, то общее решение получается в виде:
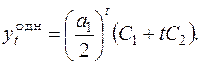
Решение носит “взрывной” характер, если 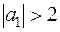 . Если
. Если 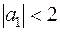 , то из-за слагаемого
, то из-за слагаемого 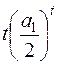 поведение общего решения не так ясно. В итоге решение стремится к нулю, но вначале может носить “взрывной” характер.
поведение общего решения не так ясно. В итоге решение стремится к нулю, но вначале может носить “взрывной” характер.
3. Если 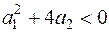 , то
, то 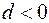 и характеристические корни комплексные. В этом случае однородное решение может быть получено в виде
и характеристические корни комплексные. В этом случае однородное решение может быть получено в виде 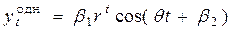 , где
, где 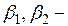 произвольные постоянные,
произвольные постоянные, 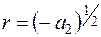 , а
, а 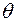 удовлетворяет соотношению
удовлетворяет соотношению 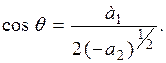 Тригонометрическая функция создает волнообразное поведение решения однородного уравнения. Частота колебаний определяется параметром
Тригонометрическая функция создает волнообразное поведение решения однородного уравнения. Частота колебаний определяется параметром 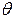 . Амплитуда колебаний определяется множителем
. Амплитуда колебаний определяется множителем 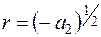 . Если
. Если  , то амплитуда не меняется. Колебания затухают при
, то амплитуда не меняется. Колебания затухают при  и растут при
и растут при 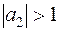 .
.
Характеризация условий устойчивости. В случае существования двух корней характеристического уравнения для устойчивости требуется, чтобы оба корня находились внутри промежутка (-1.1). В случае совпадающих характеристических корней условие устойчивости принимает вид 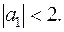 Для комплексных корней в случае 3 (
Для комплексных корней в случае 3 (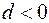 ) условие устойчивости следующее:
) условие устойчивости следующее: