Текст задания:
1. Используя знаний и умения математического анализа, для функции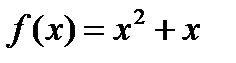 
найти первообразную, график которой проходит через точку А(1;2).
2. Вероятность того, что аудитор допустит ошибку при проверке бухгалтерского баланса, равна 10%. Аудитору на заключение представлено n=4 баланса. Получить закон распределения дискретной случайной величины X – числа правильных заключений на проверяемые балансы.
3. Используя знания и умения геометрии, вычислить высоту пирамиды, каждое боковое ребро которой равно 13 см, а стороны прямоугольного основания равны 6 см и 8 см. Построить чертеж.
Вопросы
1. Описать ход первичной статистической обработки числовых данных исследования.
2. Определить с помощью чертежа понятие «двугранный угол».
Условия выполнения задания:
1. Место (время) выполнения задания: задание выполняется в аудитории № 309 с 900 до 1100.
2. Максимальное время выполнения задания 120 минут.
3. Вы можете воспользоваться: калькулятором, макетами фигур стереометрии.
Пакет экзаменатора
2.1 Система оценки решения задач, ответов на вопросы, выполнения заданий
Без ошибок - отлично
Не более 2-х неточностей/ошибок - хорошо
3-4 ошибки - удовлетворительно
Более 4-х ошибок, нераскрытие темы, невыполнение задания, - неудовлетворительно
Средняя оценка выставляется экзаменатором по медиане оценок за каждое решение задания (ответ на вопрос).
2.2 Эталоны решения экзаменационных задач 2 семестра по математике.
Эталон к заданиям № 1.
1.1. Используя знания и умения математического анализа, проанализировать функцию 
на монотонность и экстремумы.
1)Находим область определения функции
2) Находим производную функции
3) Приравниваем производную к нулю и решаем полученное уравнение:
4) Исследуем знаки производной методом интервалов и находим интервалы монотонности функции и точки экстремума.
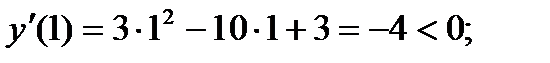
Функция возрастает на 
и убывает на 
.
Точки экстремума: 
.
5) Экстремумы функции:
1.2. Используя знания и умения математического анализа, вычислить определенные интегралы:
a) 
; b) 
.
a) 1) Запишем множество всех первообразных: tgx +c.
2) Применим формулу Ньютона-Лейбница для вычисления данного определенного интеграла:
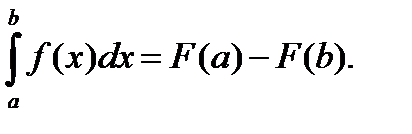
Получим
b) 1) Запишем множество всех первообразных: 
.
2) Применяем формулу Ньютона-Лейбница для вычисления данного определенного интеграла:
1.3. Используя знания и умения математического анализа, решить задачу экономической направленности. В кафе при цене 55 рублей за чашку кофе в среднем бывает 45 заказов в день. Если цену повысить до 60 рублей, то количество заказов снижается до 40 чашек кофе. Считая линейным соотношение между спросом и ценой, найти значение цены, при которой выручка достигает своего максимального значения. Каково максимальное значение выручки?
Обозначим цену чашки кофе – x, функцию спроса от цены – y(x), функцию выручки от цены – z(x).
По условию y(x) – линейная функция, поэтому y(x)=kx+b, где k и b - некоторые числа. Зная, что при цене 55 рублей за чашку кофе спрос составляет 45, а при цене 60 рублей – 40 чашек, составляем систему линейных уравнений и решаем ее методом алгебраического сложения:
Получим закон спроса: y(x)= - x+100.
Выручка определяется как произведение спроса на цену:
z=yx=(-x+100)x= -x²+100x.
Исследуем эту функцию на максимум с помощью производной.
1) Область определения функции: 
, так как цена является положительной величиной.
2) Производная функции: 
.
3) Приравниваем производную к нулю и решаем полученное уравнение:
4) Так как в этой точке знак производной меняется с плюса на минус (проверьте самостоятельно методом интервалов), то это – точка максимума.
5) Значит, в этой точке функция выручки достигает своего наибольшего значения, вычислим его:
Ответ: максимальная выручка составляет 2500 рублей в день и достигается при цене 50 рублей за одну чашку кофе.
Эталон к заданиям № 2.
2.1. Проанализировать числовые данные опроса (получить статистическое распределение выборки, вычислить моду, медиану, выборочную среднюю, дисперсию и среднеквадратическое отклонение):
2, 3, 0, 1, 1, 1, 2, 1, 4, 5.
1) Составим выборочный ряд, упорядочивая числовые данные выборки в неубывающем порядке:
0, 1, 1, 1, 1, 2, 2, 3, 4, 5.
Видим, что мода (значение с наибольшей частотой) равна Mo=1; медиана (середина выборочного ряда) равна Me=(1+2):2=1,5.
2) Составим статистическое распределение данных:
| xi | ||||||
| ni |
3) Вычислим выборочную среднюю по формуле
4) Вычислим выборочную дисперсию по формуле
5) Вычисляем среднее квадратическое отклонение по формуле
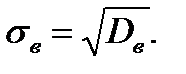
Итак, средним значением, полученным в результате опроса, является 2, причем, полученные значения отклоняются от среднего приблизительно на 1,48.
2.2. Депозитный риск (вероятность досрочного отзыва депозита) для каждого из трех клиентов банка есть величина постоянная, равная p=0,2. Получить закон распределения дискретной случайной величины X – числа отозванных депозитов.
Имеем серию n=3 независимых испытаний, в каждом из которых событие A (отзыв депозита) происходит с вероятностью p=0,2. Так как описанная в условии случайная величина X распределена по закону Бернулли, то вероятности p(X=m) того, что событие A произойдет m раз, могут быть вычислены по формуле Бернулли:
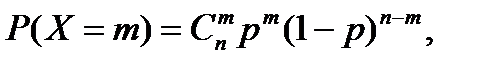
где 
- количество сочетаний из n элементов по m, определяемое комбинаторной формулой:
В нашем случае: n=3, p=0,2, поэтому:
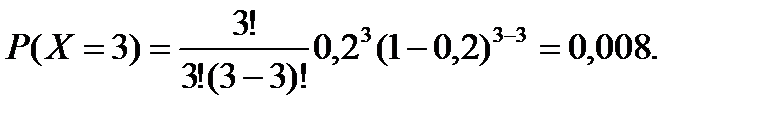
Контроль: 
Получаем закон распределения случайной величины X:
| xi | ||||
| pi | 0,512 | 0,384 | 0,096 | 0,008 |
Эталон к заданию № 3.
Используя знания и умения геометрии, вычислить диаметр чугунного шара массой m=10 кг, если плотность чугуна равна 7,2 г/см³.
1) Запишем кратко условие задачи:
Дано:
m = 10 кг =10000 г (масса);
ρ = 7,2 г/см³ (плотность).
Вычислить: d (диаметр).
2) Запишем необходимые формулы и выразим неизвестный диаметр d через известные массу m и плотность ρ.
3) По выведенной формуле вычисляем значение диаметра чугунного шара:
Ответ: диаметр чугунного шара составляет приблизительно 13,8 см.