Ответ. Предельные издержки и средние переменные издержки. 9 глава
|
Задача №1.8.22
При постоянных издержках производителя в 30 грн средние переменные издержки зависят от объема выпуска. Их величина приведена в таблице:
| Объем производства, ед.
|
|
|
|
|
|
|
|
| | Средние переменные издержки, грн.
|
|
|
|
|
|
|
|
| На основе приведенных данных:
1) Рассчитайте средние постоянные, средние общие и предельные издержки и постройте их графики и проанализируйте динамику;
2) Определите оптимальный объем выпуска продукции;.
3) Проследите эффект масштаба.
Решение
| Q
|
|
|
|
|
|
|
|
| | AVC
|
|
|
|
|
|
|
|
| | AFC
| -
|
|
|
| 7,5
|
|
| 4,3
| | AC
| -
|
|
|
| 28,5
|
|
| 46,3
| | TC
|
|
|
|
|
|
|
| 324,1
| | MC
| -
|
|
|
|
|
|
| 84,1
|
AFC = TFC / Q; AC = AFC + AVC; TC = AC*Q; MC = TCn – TC(n-1).
Поскольку общие постоянные издержки от объема выпуска не зависят, то график имеет вид горизонтальной прямой.
Кривая AFC понижается по мере того, как данная сумма постоянных издержек распределяется на все большее количество единиц продукции.
АС сначала, с увеличением объема выпуска, уменьшаются до Q = 4 ед., а затем под воздействием закона убывающей отдачи увеличиваются.
При снижении издержек АС до 4 ед. наблюдается положительный эффект масштаба, т.е. увеличение объема производимой продукции ведет к снижению затрат. Что выгодно предприятию.
При увеличении средних издержек, начиная с 5 ед. продукции, – отрицательный эффект масштаба.
К факторам, действующим в направлении снижения средних издержек производства, относятся:
а) специализация труда, в т.ч. управленческого персонала;
б) эффективное использование капитала;
в) производство побочных продуктов (утилизация отходов) и т.д.
Положительный и отрицательный эффекты масштаба используются на практике. Фирмы, преуспевающие в деле расширения масштабов своей деятельности до разумного предела, сумевшие воспользоваться положительным эффектом массового производства, выживают и процветают.
Те же, кому не удалось достичь необходимых масштабов, окажутся в проигрыше.
Кривая предельных издержек МС пересекает кривую АС в точке ее минимального значения (АС = 28,5 грн при Q = 4 ед.) – это и есть рациональный объем выпуска продукции.
Факт, что МС пересекает АСmin, объясняется тем, что пока добавочная, предельная, величина, присоединяемая к сумме общих издержек, остается меньше средней величины этих издержек, показатель средних издержек уменьшается, и наоборот.
|
|
| Задача №1.8.23
Фирма несёт постоянные издержки в размере 45000 грн (TFC).
Данные об объёмах производства и средних издержках приведены в таблице:
На основе приведённых данных:
1) Определите AFC, AC, MC, TC. Постройте кривые отражающие их динамику;
2) Объясните динамику предельных издержек.
Решение
1) рассчитаем средние постоянные издержки:
AFC = TFC / Q.
2) рассчитаем средние издержки:
AC = AVC + AFC.
3) рассчитаем общие издержки:
TC = AC*Q.
4) расчёт предельных издержек:
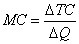 ; ;
 ; ;
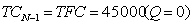 . .
При нулевом объёме выпуска продукции:

При Q = 0. AC = AFC. Переменных издержек нет.
MC при Q = 0 – нет, так как это прирост издержек на единицу продукции.
ACmin при AC = MC (*1) = 4,8 ед. Но так как мы не можем произвести нецелую единицу то оптимальный объём производства принимаем равный 4000 (шт.), что и подтверждается расчётными данными.
Вывод: До тех пор пока MC располагается ниже AC, наблюдается снижение средних издержек, следовательно производитель может увеличивать объём выпуска. Как только MC пересекает AC, наблюдается рост средних издержек. Производителю не имеет смысла увеличивать объём выпуска. Точка пересечения AC и MC – оптимальный объём выпуска, при условии, что ACmin.
|
|
| Задача №1.8.24
На конкурентном рынке с функцией спроса Q(P) = 2000 − 20P
действуют фирмы с функциями затрат TC(q) = 450 + 10q + 2q2.
Сколько фирм будет на рынке в условиях равновесия длительного периода?
Решение
В равновесии длительного периода устанавливается цена, равная минимуму средних затрат каждой из фирм. Средние затраты принимают минимальное значение при объеме производства, при котором они равны предельным затратам, AC(q) = MC(q), т.е. для нашей задачи: 450/q + 10 + 2q = 10 + 4q, откуда находим минимально эффективный размер производства типичной фирмы рынка:
q = √450/2 = 15.
Подставив в формулу средних или предельных издержек это значение выпуска, получаем: AC = MC = 70.
Этот уровень соответствует долгосрочной рыночной цене: P = 70.
Теперь подставим значение цены в функцию рыночного спроса.
Объем спроса Q = 2000 − 20 ⋅ 70 = 600.
Теперь найдем максимальное число фирм на рынке в долгосрочном периоде:
N = Q/q = 600/15 = 40 фирм.
Ответ. Таким образом, на рынке будет действовать 40 компаний.
Чему учит данное задание?
В задании находят оптимальное число компаний для долгосрочного периода.
Видно, что на число фирм оказывает влияние не только производственная часть – издержки и минимально эффективный размер выпуска, но и рыночная сторона – функция спроса.
|
|
Задача №1.8.25
Найти оптимальный объём производства фирмы,
функция прибыли которой задана таким образом:
П(q) = TR(q) – TC(q) = q2 – 8q + 10.
Решение
Найдём производную данной функции:
П  Приравняем производную к нулю и найдём точку экстремума:
П
Приравняем производную к нулю и найдём точку экстремума:
П  Является ли объём выпуска, равный четырём единицам продукции, оптимальным для фирмы? Чтобы ответить на этот вопрос, надо проанализировать характер изменения знака производной при переходе через точку экстремума.
При
Является ли объём выпуска, равный четырём единицам продукции, оптимальным для фирмы? Чтобы ответить на этот вопрос, надо проанализировать характер изменения знака производной при переходе через точку экстремума.
При  П П  и прибыль убывает.
При и прибыль убывает.
При 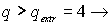 П П  и прибыль возрастает.
Как видим, при переходе через точку экстремума производная меняет свой знак с минуса на плюс. Следовательно, в точке экстремума и прибыль возрастает.
Как видим, при переходе через точку экстремума производная меняет свой знак с минуса на плюс. Следовательно, в точке экстремума  прибыль принимает минимальное значение, и таким образом, этот объём производства не является оптимальным для фирмы.
Каким же всё-таки будет оптимальный объём выпуска для данной фирмы?
Ответ на этот вопрос зависит от дополнительного исследования производственных возможностей фирмы.
Если фирма не может производить за рассматриваемый период больше 8 единиц продукции (П(q = 8) = П(q = 0) = 10), то оптимальным решением для фирмы будет вообще ничего не производить, а получать доход от сдачи в аренду помещений и/или оборудования.
Если же фирма способна производить за рассматриваемый период больше 8 единиц продукции, то оптимальным решением для фирмы будет выпуск на пределе своих производственных возможностей. прибыль принимает минимальное значение, и таким образом, этот объём производства не является оптимальным для фирмы.
Каким же всё-таки будет оптимальный объём выпуска для данной фирмы?
Ответ на этот вопрос зависит от дополнительного исследования производственных возможностей фирмы.
Если фирма не может производить за рассматриваемый период больше 8 единиц продукции (П(q = 8) = П(q = 0) = 10), то оптимальным решением для фирмы будет вообще ничего не производить, а получать доход от сдачи в аренду помещений и/или оборудования.
Если же фирма способна производить за рассматриваемый период больше 8 единиц продукции, то оптимальным решением для фирмы будет выпуск на пределе своих производственных возможностей.
|
|
| Задача №1.8.26
Даны функция спроса на продукцию монополиста Q = 25 – P
и функция средних переменных затрат AVC = 4 + 0,5 × Q.
Известно, что максимум прибыли монополиста равен 23,5.
Найти его фиксированные затраты.
Решение
Фиксированные затраты входят в состав общих затрат (TC).
ТС = FC + VC,
Где FC – фиксированные затраты, VC – переменные затраты.
Зная средние переменные затраты, можно найти переменные затраты по формуле:
VC = AVC × Q
Величина общих затрат входит в формулу прибыли фирмы:
П = TR – TC,
Где TR – общий доход, который равен произведению цены и объёма производства.
TR = P × Q
Тогда формула прибыли будет иметь вид:
П = P × Q – (FC + AVC × Q)
Подставим все имеющиеся данные, цену выразим из функции спроса
Р = 25 – Q:
23,5 = (25 – Q) × Q – (FC + (4 + 0,5 × Q) × Q)
23,5 = 25 × Q – Q2 – FC – 4 × Q – 0,5 × Q2
Отсюда выразим фиксированные затраты:
FC = 21 × Q – 1,5 × Q2 – 23,5
Теперь определим оптимальный объём производства монополиста.
Для этого воспользуемся условием максимизации прибыли:
МС = MR
Найдём функцию предельных издержек.
Возьмём производную функции общих затрат:
МС = ТС' = (FC + (4 + 0,5 × Q) × Q)' = (FC + 4 × Q + 0,5 × Q2)'
Производная от константы (от фиксированных затрат) равна нулю.
Таким образом,
МС = 4 + Q
Функция предельного дохода равна производной от функции общего дохода:
MR = TR' = (P × Q)' = ((25 – Q) × Q)' = (25 × Q – Q2)' = 25 – 2 × Q
Приравняем функции MC и MR:
4 + Q = 25 – 2 × Q
3 × Q = 21
Q = 7 – оптимальный выпуск фирмы монополиста.
Ответ.Следовательно, фиксированные затраты будут равны:
FC= 21 × 7 – 1,5 × 72 – 23,5 = 147 – 73,5 – 23,5 = 50
|
|
Задача №1.8.27
Функция спроса на продукцию монополиста:
P = 20 – 2 × Q.
MC = AC = 4.
Найти эластичность спроса по цене, если монополист ищет максимум прибыли.
Решение
Эластичность спроса по цене рассчитывается по формуле:  ,
где ,
где
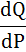 – производная функции спроса Q(P) по аргументу Р.
По условию задачи функция спроса на продукцию монополиста:
P = 20 – 2 × Q.
Это обратная функция спроса.
Выразив отсюда Q, получим прямую функцию спроса:
Q = 10 – 0,5 × P,
производная которой и потребуется нам при нахождении эластичности спроса по цене. – производная функции спроса Q(P) по аргументу Р.
По условию задачи функция спроса на продукцию монополиста:
P = 20 – 2 × Q.
Это обратная функция спроса.
Выразив отсюда Q, получим прямую функцию спроса:
Q = 10 – 0,5 × P,
производная которой и потребуется нам при нахождении эластичности спроса по цене.
 Осталось найти координаты точки оптимума. То есть такой оптимальный объём производства и цену, при которых монополист максимизирует свою прибыль.
Условие максимизации прибыли на рынке несовершенной конкуренции имеет вид:
MC = MR
Предельные издержки по условию равны:
MC = 4.
Найдём величину общего дохода по формуле:
TR = Р × Q = (20 – 2 × Q) × Q = 20 × Q – 2 × Q2
Тогда предельный доход будет равен:
MR = TR' = (20 × Q - 2 × Q2)' = 20 – 4 × Q
4 = 20 – 4 × Q
Q = 4 – это оптимальный объём выпуска монополиста.
Цену найдём из функции спроса:
P = 20 - 2 × 4 = 12.
Рассчитаем эластичность спроса по цене:
Осталось найти координаты точки оптимума. То есть такой оптимальный объём производства и цену, при которых монополист максимизирует свою прибыль.
Условие максимизации прибыли на рынке несовершенной конкуренции имеет вид:
MC = MR
Предельные издержки по условию равны:
MC = 4.
Найдём величину общего дохода по формуле:
TR = Р × Q = (20 – 2 × Q) × Q = 20 × Q – 2 × Q2
Тогда предельный доход будет равен:
MR = TR' = (20 × Q - 2 × Q2)' = 20 – 4 × Q
4 = 20 – 4 × Q
Q = 4 – это оптимальный объём выпуска монополиста.
Цену найдём из функции спроса:
P = 20 - 2 × 4 = 12.
Рассчитаем эластичность спроса по цене:

|
|
Задача №1.8.28
Заполните таблицу, рассчитав недостающие данные.
| Количество продукции Q
| Совокупные издержки TC
| Постоянные издержки TFC
| Переменные издержки TVC
| Средние совокупные издержки ATC
| Предельные издержки MC
| Совокупный доход TR
| Средние совокупный доход AR
| Предельный доход MR
| Цена единицы продукции P
| Прибыль (убытки)
| |
|
| | | | | | | |
| | |
| | | | |
|
| | | | | |
| | | |
| | |
| | | | |
| | |
| | | | |
| | | |
|
| | | | | | | |
| |
Решение
Для расчета необходимо воспользоваться формулами:
ТС = ТFC + TVC, ATC = TC/Q, MC = TCn – TCn-1, TR = P*Q, AR = TR/Q, MR = TRn – TRn-1, Прибыль = TR – TC.
| Количество продукции Q
| Совокупные издержки TC
| Постоянные издержки TFC
| Переменные издержки TVC
| Средние совокупные издержки ATC
| Предельные издержки MC
| Совокупный доход TR
| Средние совокупный доход AR
| Предельный доход MR
| Цена единицы продукции P
| Прибыль (убытки)
| |
|
|
|
|
| -
|
| -
| -
|
| -15
| |
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| |
|
| Задача №1.8.29
Даны функции общих издержек и выручки монополиста:
ТС = ½Q² + 20Q + 90;
TR = 140Q – 3/2 Q².
Определите ценовую эластичность рыночного спроса в точке максимальной прибыли.
Ответ: 2,1.
| |
| Задача №1.8.30
Задача из А. Султыговой.
Найдем ценовую эластичность рыночного спроса монополиста в точке максимальной прибыли, если он, действуя наилучшим для себя образом и обладая полной информацией, назначает цену на уровне: P = 52 – 2Q.
При этом общие издержки на произвоство продукции составляют:
TC = 120 – 8Q + Q².
Решение
Для определения ценовой эластичности рыночного спроса монополиста воспользуемся коэффициентом Лернера (L):
(P – MC) / P = 1 / |Ed|.
По условию задачи мы располагаем функциями цены и общих издержек фирмы. Следовательно, определив объём производства, при котором фирма – монополист получает максимум прибыли, мы сможем найти соответствующее значение цены и рассчитать ценовую эластичность рыночного спроса.
Первый способ:
а) Определим объём производства, максимизирующий прибыль, используя правило максимизации MR = MC.
MR = (TR)’ = (P×Q)’= ((52 – 2Q) × Q)' = (52Q – 2Q²)' = 52 – 4Q;
MC = (TC)’ = (120 – 8Q + Q²)' = 2Q – 8.
Приравняем значения соответствующих выражений MR и MC.
Мы получим следующее выражение: 52 – 4Q = 2Q – 8. Отсюда, объём продукции, максимизирующий прибыль монополиста, составит 10 ед.
б) Монопольная цена фирмы в точке, максимизирующей прибыль, должна быть равна величине среднего дохода (AR).
Рассчитаем величину среднего дохода по формуле:
AR = TR / Q, где TR = 52Q – 2Q², а Q = 10.
Отсюда, величина среднего дохода составит:
AR = 32 ден. ед. (52Q – 2 Q²) / Q = 52 – 2Q = 52 – 2 × 10.
Тогда монопольная цена фирмы (P) будет 32 (так как AR = 32).
в) Определим величину предельных издержек MC = 2Q – 8
в точке, максимизирующей прибыль. Мы получим: MC = 2 × 10 – 8 = 12.
г) Для определения ценовой эластичности рыночного спроса монополиста воспользуемся индексом Лернера (L):
(P – MC) / P = 1 / |Ed|.
(32 – 12) / 32 = 1 / |Ed|
1,6 = 1 / |Ed| = Ed = 1,6.
Второй способ:
По условию задачи, мы располагаем функциями монопольной цены и общих издержек монополиста. Для того, чтобы найти ценовую эластичность рыночного спроса в точке максимальной прибыли, мы должны знать величину монопольной цены и предельных издержек.
а) Вычислим величину монопольной цены P = 52 – 2Q.
Из формулы цены мы видим, что нам не хватает значения объёма производства (Q), максимизирующего прибыль. Для его исчисления воспользуемся формулой прибыли PR = TR – TC, где TR = P × Q.
Если мы приравняем производную функции прибыли к нулю, то сможем определить объём производства, максимизирующий прибыль.
Запишем формулу прибыли:
PR = (52 – 2Q) × Q – (120 - 8Q + Q²) = 52Q – 2Q² – (120 – 8Q + Q²) =>
PR = 60Q – 3Q² – 120.
Приравняем производную функции прибыли к нулю и определим объём производства, максимизирующий прибыль:
(PR)' = (60Q – 3Q² – 120)' = 60 – 6Q.
60 – 6Q = 0;
Q = 10 ед.
Отсюда, величина монопольной цены P = 52 – 2×10 = 32 ден. ед.
б) Найдем значение предельных издержек.
Функция предельных издержек есть первая производная общих издержек:
MC = (TC)’ = (120 – 8Q + Q²)' = 2Q – 8.
Если мы подставим значение объема производства, максимизирующего прибыль, в формулу функции предельных издержек, то получим соответствующее значение:
MC = 2Q – 8 = 2×10 – 8 = 12.
в) Ценовую эластичность рыночного спроса Ed рассчитаем по формуле:
(P – MC) / P = 1 / |Ed|.
(32 – 12) / 32 = 1 / |Ed|;
20 / 32 = 1 / |Ed|;
Ed = 1,6.
Ответ: Ed = 1,6.
Чем более эластичен спрос, тем меньшей рыночной властью обладает фирма.
|
|
| Задача №1.8.31
Продаваемая продукция приносит выручку производителям в размере:
А) TR = 9Q;
Б) MR = 3;
В) TR = 8Q – ¼ Q²;
Г) MR = 7 – 0,5Q.
Определим тип рыночной структуры в каждом из этих случаев.
Решение
Из всего многообразия признаков, отличающих один тип рыночной структуры от другого, воспользуемся главным признаком – ценовым.
По ценовому признаку мы можем судить, в какой мере продавец обладает рыночной властью. В частности, в условиях совершенной конкуренции цена не зависит от объёма продаж, а при несовершенной конкуренции – зависит.
В микроэкономике, если прямая функция спроса описывает зависимость величины спроса от цены (Q(D) = b – aP), то обратная функция цены спроса от величины спроса будет выглядеть следующим образом: (P = b / а – Q / a).
Применительно к условию нашей задачи мы имеем следующее:
А) TR = 9×Q; => P×Q = 9×Q; а P = 9.
Б) MR = 3; тогда TR = 3×Q или P×Q = 3Q; => P = 3.
В) TR = 8Q – ¼Q²; тогда P×Q = 8Q – ¼Q²; => P = 8 – ¼Q.
Г) MR = 7 – ½Q; тогда TR = 7Q –¼Q² или P×Q = 7Q – ¼Q²; => P = 7 – ¼Q.
Ответ
А); Б) – случай совершенной конкуренции, т.к. цена не зависит от объёма продаж;
В); Г) – случай несовершенной конкуренции, т.к. цена зависит от объема продаж.
|
|
| Задача №1.8.32
Юный экономист, анализируя деятельность совершенно конкурентной фирмы, максимизирующей прибыль, нарисовал график, где, по неопытности, допустил некоторые ошибки.
Найдите и объясните (!) максимальное количество неточностей на представленном ниже графике, исходя из стандартных предпосылок, относительно производственной функции и целей фирмы:
Решение
Необходимо обнаружение «ошибки» с обьяснением:
1) AFC пересекает ось Р.
2) МС пересекает AC не в точке минимума последней.
3) AVC и АС не сближаются с ростом Q и расстояние между ними не равно AFC.
4) Закрашенная площадь является прибылью, но не соответствует оптимальному объему выпуска с точки зрения максимизации прибыли, плюс к этому при таком расположении Р и АС логичнее было бы написать, что это не «прибыль», а «убытки».
5) Точка Q = 0 на кривых МС и AVC не выколота.
|
|
Задача №1.8.33
Функция издержек совершенно конкурентной фирмы описывается уравнением:
 а) При какой минимальной рыночной цене фирма останется на рынке в краткосрочном периоде?
б) Интерпретируйте ответ графически.
Решение
Искомая цена равна
а) При какой минимальной рыночной цене фирма останется на рынке в краткосрочном периоде?
б) Интерпретируйте ответ графически.
Решение
Искомая цена равна  Восстановим функцию
Восстановим функцию  Внимание! Неверно считать, что
Внимание! Неверно считать, что  Постоянные издержки, по определению, не зависят от выпуска и равны
Постоянные издержки, по определению, не зависят от выпуска и равны 

 .
Значит, .
Значит,  .
При .
При  данная функция линейна, монотонно возрастает и достигает минимума при данная функция линейна, монотонно возрастает и достигает минимума при  ; ;  При
При  исследуем нашу функцию с помощью производной: исследуем нашу функцию с помощью производной:
 – точка локального минимума нашей функции. – точка локального минимума нашей функции.
 Значит,
Значит, 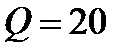 является также и точкой глобального минимума данной функции, и является также и точкой глобального минимума данной функции, и  , что соответствует искомому значению цены.
б) 1-й способ иллюстрации.
График функции , что соответствует искомому значению цены.
б) 1-й способ иллюстрации.
График функции  будет в нашем случае иметь вид: будет в нашем случае иметь вид:
2-й способ иллюстрации.
График предельных издержек МС(Q) в нашем случае будет иметь вид:
Ответ: а) цена равна 8.
|
|
| Задача №1.8.34
Вопрос из А. Султыговой.
В гипотетической экономике наблюдается процесс концентрации предприятий и производства. Это связано как с открытием новых предприятий, так и с укрупнением, слиянием мелких хозяйствующих единиц.
Собранная по итогам года статистика показала, что ряд предприятий в различных отраслях заняла долю рынка, свыше 35%.
Используя меры антимонопольной политики, установите соответствие между видами мер и их содержанием:
1) административно-правовое воздействие;
2) административно-экономическое воздействие;
3) экономическое воздействие.
Варианты ответа:
1) выпуск товаров-субститутов, расширение внутреннего рынка за счет импорта товаров;
2) принудительное разделение предприятий, которые занимают значительную долю рынка;
3) структурная перестройка экономики путем разгосударствления и приватизации.
Ответ
Подзадача 1.
Основные группы мер антимонопольной политики:
1) административно-правовое воздействие:
запрет на существование монополий в различных отраслях хозяйства;
разделение существующих предприятий на ряд независимых единиц;
2) административно-экономическое воздействие:
запрещение ценовой дискриминации, пресечение недобросовестной (нечестной) конкуренции; запрещение сговора между предприятиями с целью пресечения совместного влияния на рыночную ситуацию;
3) экономическое воздействие:
применение различных приемов налоговой политики, которые заставят монополию назначать цены на свою продукцию, близкие к свободно конкурентным ценам; стимулирование выпуска взаимозаменяемых товаров (товаров-субститутов); расширение рынка за счет импортных товаров.
Подзадача 2.
Проведение политики демонополизации, основными целями которой являются:
создание равных условий функционирования для субъектов различных форм собственности, нейтрализация барьеров для конкуренции;
увеличение выпуска товаров, конкурирующих с дефицитом на рынке за счет увеличения количества производителей в «проблемных» отраслях и т.п.
|
|
| Задача №1.8.35
Длина города равна 35 км. Магазин первого дуополиста расположен в точке А на расстоянии 4 км от левого конца города (точка М). Магазин второго – в точке В на расстоянии 1 км от правого конца города. Стоимость перевозки равно 1 ден. ед. на км. Дуополисты максимизируют выручку. Потребители проживают равномерно по всей длине города. Найти расположение точки Е, в которой проживает потребитель, затраты которого на покупку единицы товара (включающие транспортные расходы) одинаковы для обоих магазинов.
Решение
Найдем расположение точки Е, в которой находится потребитель и где затраты на покупку единицы товара, включая транспортные расходы, одинаковы для обоих магазинов. Если через x и y обозначить расстояния от безразличного покупателя до первого и второго магазина соответственно, то условие безразличия примет вид: P1 + x = P2 + y и, кроме того:4 + 1 + x + y = 35.
Решив совместно эти два уравнения относительно x и y, получим:
x = 15 + 0,5(P1 – P2), y = 15 – 0,5(P2 – P1).
Обозначим объем продаж каждого дуополиста через Q1 и Q2.
Тогда: Q1 = x + 4 и Q2 = y + 1.
Выручка первого равна: TR1 = P1Q1 = 19 P 1 + 0,5 P1P 2 – 0,5 P2 2.
Она достигает максимума, когда P1 – 0,5 P2 – 19 = 0. (1)
Аналогично для второй фирмы, составив функцию выручки и взяв производную по P2 получаем: –0,5 P1 + P2 – 16 = 0. (2)
Решив систему уравнений (1) и (2) находим цены: P1 = 36; P2 = 34.
Тогда легко найти x и y: x = 15 + 0,5×2 = 16 км, y = 15 – 0,5×2 = 14 км.
|
|
Задача №1.8.36
Из Т. Болочагиной
Крах коммунистической системы превратил СССР в рай для первоначального накопления капитала. Громадные состояния наживались в мгновение ока.
Особое значение имели четыре метода присвоения «ренты»: спекуляция, субсидии на импорт, льготные кредиты, номенклатурная приватизация.
Расскажите об этих методах подробнее.
Ответ (трактовка темы принадлежит автору вопроса)
Спекуляция.
После 1987 г. она стала главным делом для кооперативов, которые покупали все что угодно за бесценок по государственной цене, а затем продавали дорого – по рыночной. Но «золотую ренту» получили те, кто имел доступ к нефти, газу и металлу. Они покупали их по цене, составляющей менее 1% рыночной, а продавали за рубежом по ценам мирового рынка.
|
Поиск по сайту:
|



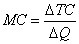 ;
; ;
;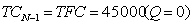 .
.

 Приравняем производную к нулю и найдём точку экстремума:
П
Приравняем производную к нулю и найдём точку экстремума:
П  Является ли объём выпуска, равный четырём единицам продукции, оптимальным для фирмы? Чтобы ответить на этот вопрос, надо проанализировать характер изменения знака производной при переходе через точку экстремума.
При
Является ли объём выпуска, равный четырём единицам продукции, оптимальным для фирмы? Чтобы ответить на этот вопрос, надо проанализировать характер изменения знака производной при переходе через точку экстремума.
При  П
П  и прибыль убывает.
При
и прибыль убывает.
При 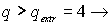 П
П  и прибыль возрастает.
Как видим, при переходе через точку экстремума производная меняет свой знак с минуса на плюс. Следовательно, в точке экстремума
и прибыль возрастает.
Как видим, при переходе через точку экстремума производная меняет свой знак с минуса на плюс. Следовательно, в точке экстремума  прибыль принимает минимальное значение, и таким образом, этот объём производства не является оптимальным для фирмы.
Каким же всё-таки будет оптимальный объём выпуска для данной фирмы?
Ответ на этот вопрос зависит от дополнительного исследования производственных возможностей фирмы.
Если фирма не может производить за рассматриваемый период больше 8 единиц продукции (П(q = 8) = П(q = 0) = 10), то оптимальным решением для фирмы будет вообще ничего не производить, а получать доход от сдачи в аренду помещений и/или оборудования.
Если же фирма способна производить за рассматриваемый период больше 8 единиц продукции, то оптимальным решением для фирмы будет выпуск на пределе своих производственных возможностей.
прибыль принимает минимальное значение, и таким образом, этот объём производства не является оптимальным для фирмы.
Каким же всё-таки будет оптимальный объём выпуска для данной фирмы?
Ответ на этот вопрос зависит от дополнительного исследования производственных возможностей фирмы.
Если фирма не может производить за рассматриваемый период больше 8 единиц продукции (П(q = 8) = П(q = 0) = 10), то оптимальным решением для фирмы будет вообще ничего не производить, а получать доход от сдачи в аренду помещений и/или оборудования.
Если же фирма способна производить за рассматриваемый период больше 8 единиц продукции, то оптимальным решением для фирмы будет выпуск на пределе своих производственных возможностей.
 ,
где
,
где
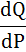 – производная функции спроса Q(P) по аргументу Р.
По условию задачи функция спроса на продукцию монополиста:
P = 20 – 2 × Q.
Это обратная функция спроса.
Выразив отсюда Q, получим прямую функцию спроса:
Q = 10 – 0,5 × P,
производная которой и потребуется нам при нахождении эластичности спроса по цене.
– производная функции спроса Q(P) по аргументу Р.
По условию задачи функция спроса на продукцию монополиста:
P = 20 – 2 × Q.
Это обратная функция спроса.
Выразив отсюда Q, получим прямую функцию спроса:
Q = 10 – 0,5 × P,
производная которой и потребуется нам при нахождении эластичности спроса по цене.
 Осталось найти координаты точки оптимума. То есть такой оптимальный объём производства и цену, при которых монополист максимизирует свою прибыль.
Условие максимизации прибыли на рынке несовершенной конкуренции имеет вид:
MC = MR
Предельные издержки по условию равны:
MC = 4.
Найдём величину общего дохода по формуле:
TR = Р × Q = (20 – 2 × Q) × Q = 20 × Q – 2 × Q2
Тогда предельный доход будет равен:
MR = TR' = (20 × Q - 2 × Q2)' = 20 – 4 × Q
4 = 20 – 4 × Q
Q = 4 – это оптимальный объём выпуска монополиста.
Цену найдём из функции спроса:
P = 20 - 2 × 4 = 12.
Рассчитаем эластичность спроса по цене:
Осталось найти координаты точки оптимума. То есть такой оптимальный объём производства и цену, при которых монополист максимизирует свою прибыль.
Условие максимизации прибыли на рынке несовершенной конкуренции имеет вид:
MC = MR
Предельные издержки по условию равны:
MC = 4.
Найдём величину общего дохода по формуле:
TR = Р × Q = (20 – 2 × Q) × Q = 20 × Q – 2 × Q2
Тогда предельный доход будет равен:
MR = TR' = (20 × Q - 2 × Q2)' = 20 – 4 × Q
4 = 20 – 4 × Q
Q = 4 – это оптимальный объём выпуска монополиста.
Цену найдём из функции спроса:
P = 20 - 2 × 4 = 12.
Рассчитаем эластичность спроса по цене:

 а) При какой минимальной рыночной цене фирма останется на рынке в краткосрочном периоде?
б) Интерпретируйте ответ графически.
Решение
Искомая цена равна
а) При какой минимальной рыночной цене фирма останется на рынке в краткосрочном периоде?
б) Интерпретируйте ответ графически.
Решение
Искомая цена равна  Восстановим функцию
Восстановим функцию  Внимание! Неверно считать, что
Внимание! Неверно считать, что  Постоянные издержки, по определению, не зависят от выпуска и равны
Постоянные издержки, по определению, не зависят от выпуска и равны 

 .
Значит,
.
Значит,  .
При
.
При  данная функция линейна, монотонно возрастает и достигает минимума при
данная функция линейна, монотонно возрастает и достигает минимума при  ;
;  При
При  исследуем нашу функцию с помощью производной:
исследуем нашу функцию с помощью производной:
 – точка локального минимума нашей функции.
– точка локального минимума нашей функции.
 Значит,
Значит, 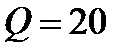 является также и точкой глобального минимума данной функции, и
является также и точкой глобального минимума данной функции, и  , что соответствует искомому значению цены.
б) 1-й способ иллюстрации.
График функции
, что соответствует искомому значению цены.
б) 1-й способ иллюстрации.
График функции  будет в нашем случае иметь вид:
будет в нашем случае иметь вид:
