Ответ: максимальная прибыль фирмы в условиях совершенной конкуренции равна 120 д. ед.
|
|
Задача №1.9.7
Экономисты фирмы, производящей снегоходы, выяснили, что потенциальные покупатели делятся на две группы. Недельный спрос первой группы описывается уравнением 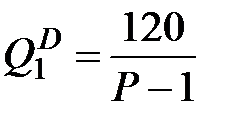 , а спрос второй группы равен , а спрос второй группы равен 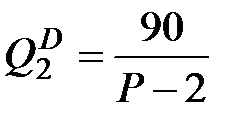 , где Р – цена снегоходов, которая по требованию правительства должна удовлетворять ограничению , где Р – цена снегоходов, которая по требованию правительства должна удовлетворять ограничению 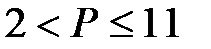 . Фирма способна произвести за неделю не более 60 снегоходов, причем издержки фирмы постоянны и равны TC = 200.
Определите максимальную прибыль, которую может получить фирма, если она не проводит ценовой дискриминации?
Решение
Обозначим выручку фирмы от продажи товара покупателям первой и второй группы через TR1 и TR2.
Из уравнений кривых спроса получим: . Фирма способна произвести за неделю не более 60 снегоходов, причем издержки фирмы постоянны и равны TC = 200.
Определите максимальную прибыль, которую может получить фирма, если она не проводит ценовой дискриминации?
Решение
Обозначим выручку фирмы от продажи товара покупателям первой и второй группы через TR1 и TR2.
Из уравнений кривых спроса получим:  ; ;  .
Прибыль фирмы равна: .
Прибыль фирмы равна: 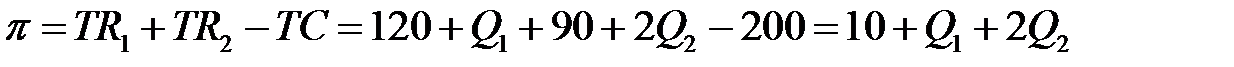 .
Если фирма не проводит ценовую дискриминацию, то задача максимизации прибыли сводится к нахождению такой цены, при которой .
Если фирма не проводит ценовую дискриминацию, то задача максимизации прибыли сводится к нахождению такой цены, при которой  и выполняются ограничения и выполняются ограничения  , ,  , ,  , , 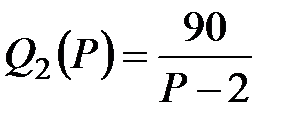 .
Поскольку функции спроса убывают с ростом цены на исследуемом интервале цен, то ограничение .
Поскольку функции спроса убывают с ростом цены на исследуемом интервале цен, то ограничение  не может выполняться в оптимуме как строгое неравенство, т.к. иначе можно немного уменьшить цену, соответственно не может выполняться в оптимуме как строгое неравенство, т.к. иначе можно немного уменьшить цену, соответственно 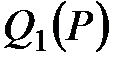 и и 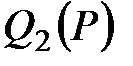 увеличатся и прибыль возрастет. Поэтому ищем оптимальное решение, предполагая равенство увеличатся и прибыль возрастет. Поэтому ищем оптимальное решение, предполагая равенство 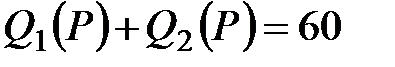 , т.е. , т.е.  . Отсюда получаем квадратное уравнение . Отсюда получаем квадратное уравнение  . Корни уравнения равны . Корни уравнения равны  и и 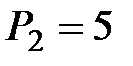 .
В необходимый интервал попадает второй корень, поэтому оптимальная цена .
В необходимый интервал попадает второй корень, поэтому оптимальная цена  . При этом покупки покупателей первой и второй группы равны . При этом покупки покупателей первой и второй группы равны  , ,  , и фирма получает прибыль , и фирма получает прибыль 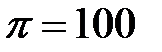 .
Ответ: .
Ответ: 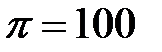 . .
|
|
| Задача №1.9.8
На рынке манны небесной спрос зависит от рекламных вложений и выражается соотношением p = 1− q(1− a). Здесь p – цена за 1 г, тыс. руб., q – объем продаж, тонн, 0 ≤ a ≤ 1 – затраты на рекламу, млрд руб.
Себестоимость добычи не зависит от объема и составляет 500 руб. за 1 г.
При каком объеме рекламных вложений можно получить максимальную прибыль?
Решение
Задачу можно решать, выписав функцию прибыли:
π = (p − 0,5)q − a = (1 − q(1 − a) − 0,5)q − a → max,
найдя оптимальный объем добычи при каждом уровне рекламных вложений и затем исследовав функцию прибыли от оптимального объема добычи на максимум по одной переменной: уровню рекламных вложений.
Однако проще заметить, что при равенстве рекламных вложений 1 млрд руб. уравнение спроса принимает вид p = 1, т.е. по цене 1 тыс. руб. за 1 г можно продать неограниченное количество продукции. Поскольку себестоимость составляет 500 руб., что меньше продажной цены, можно получить неограниченную прибыль.
|
|
| Задача №1.9.9
Собственник фермерского хозяйства, выращивающего пшеницу, считает, что его бизнес нерентабелен, несмотря на рост объемов производства, и планирует закрыть фирму. Известно, что неявные издержки равны нулю, а годовые бухгалтерские затраты фирмы на производство пшеницы включают в себя:
· оплату лизинговых платежей за сельскохозяйственное оборудование в размере 45 тыс. руб.;
· уплату земельного налога в сумме 9 тыс. руб.;
· выплату заработной платы рабочим в размере 1,2 тыс. руб. (с учетом социальных взносов) в расчете на каждую тонну произведенной пшеницы;
· оплату труда директора (30 тыс. руб. в месяц) и бухгалтера (20 тыс. руб. в месяц); · ежемесячные выплаты по банковскому кредиту в размере 4 тыс. руб.;
· покупку горюче-смазочных материалов в расчете 0,4 тыс. руб. на каждые 0,5 тонн произведенной пшеницы.
Кроме того, в целях сохранения урожая, производятся работы по борьбе с вредителями. Как было замечено, эти затраты могут быть выражены возрастающей квадратичной функцией: 0,05Q2 (где Q – количество произведенной пшеницы в тоннах). Рыночная цена тонны пшеницы составляет 10 тыс. руб. Фирма за отчетный период произвела и реализовала 100 тонн пшеницы.
При условии, что цена пшеницы и цены факторов производства остаются неизменными, а фирма стремится получить максимальную прибыль (или минимизировать убыток), что Вы посоветуете собственнику:
а) продолжать производить прежний объем пшеницы, обеспечивающий фирме максимальную прибыль (минимальный убыток);
б) изменить объем производства таким образом, чтобы обеспечить максимальную прибыль (минимальный убыток)?
Обоснуйте свой ответ и приведите соответствующие расчеты.
Решение
1) Найдём прибыль фермы при объёме производства 100 т.
Общие издержки производства за год:
45 + 9 + 1,2Q + 30×12 + 20×12 + 4×12 + 0,4×2×Q + 0,05Q2 = 702 + 2×Q + 0,05Q2 = 702 + 2×100 + 0,05×1002 = 1 402 тыс. рублей.
Выручка фермы за год = 10×Q = 10×100 = 1 000 тыс. рублей.
Прибыль фермы за год при объёме производства 100 т:
Выручка – Общие издержки = 1 000 – 1 402 = (-402) тыс. рублей.
Заметим, что величина постоянных издержек = 702 тыс. рублей.
2) Выясним, производит ли фирма оптимальный объём выпуска, при котором прибыль будет максимальна.
Для этого исследуем функцию прибыли на экстремум.
Функция прибыли имеет вид:
Прибыль (Q) = 10×Q – (702 + 2×Q + 0,05Q2) = 8×Q – 702 – 0,05Q2:
парабола, ветви которой направлены вниз.
Поэтому вершина параболы является точкой максимума.
Вершина параболы находится в точке Q = 80.
Максимально возможную прибыль фирма получит, если будет производить Q = 80.
Этот же ответ можно было получить, продифференцировав функцию прибыли по Q и приравняв её к нулю.
Фирма, производя 80 т пшеницы, несёт минимально возможные убытки (-382).
Величина постоянных издержек = 702 тыс. рублей. Фирма, производя 80 т пшеницы, несёт убытки меньшие, чем постоянные издержки.
Вывод:
Фирме не следует прекращать производство.
Но необходимо сократить объём производства до 80 т.
Ответ
1) нет, убыток = 602 тыс. руб.;
2) да, сократить объемы производства;
3) Q = 80 тонн.
|
|
| Задача №1.9.10
Фирма Винтик&Co продает винтики по цене за штуку и является монополистом на этом рынке. Спрос на винтики задается функций Q = 360 – P.
Главной деталью для изготовления каждого винтика являются шпунтик, и кроме как стоимость шпунтика других переменных издержек не требуется.
Винтик&Со закупает шпунтики у фирмы Шпунтик&Co по цене за шпунтик.
Предельные издержки изготовления одного шпунтика постоянны и равны 40, фиксированных издержек нет.
Найдитеx иy, если известно, что больше никакие другие фирмы не производят ни шпунтики, ни винтики.
Решение
Шпунтик&Со устанавливает цену на шпунтики, которую Винтик&Со воспринимает, как средние переменные издержки производства каждого винтика. Винтик&Со в свою очередь устанавливает цену на винтики, максимизируя свою прибыль:
Прибыль винтики = (360 – x) * (x – y).
Вершина параболы по формуле определяет максимум: x = (y + 360)/2.
По такой цене будет произведено и куплено: Q = (360 – y)/2 винтиков.
Для фирмы Шпунтик&Co это уравнение задаёт спрос на её продукцию.
Фирма также устанавливает цену y максимизируя свою прибыль:
Прибыль шпунтики = (y – 40) * (360 – y)/2
По формуле вершины параболы однозначно определяется y для достижения максимума прибыли.
Ответ: x = 280, y = 200.
|
|
| Задача №1.9.11
Задача из А. Султыговой.
Рассмотрим поведение фирмы-монополиста на следующем примере.
Даны функция издержек производства фирмы – монополиста и функции спроса на продукцию этой монополии на двух рынках:
TC = ¼ Q² + 10Q + 300;
Q(1) = 400 – 2P(1);
Q(2) = 600 – 4P(2).
А) Найдём объёмы продаж и цены на каждом из двух рынков, максимизирующие прибыль, при условии, что ценовая дискриминация незапрещена государством?
Б) Определим прибыль монополиста при ценовой дискриминации.
В) Как изменятся объём продаж, цены и прибыль, если ценовая дискриминация запрещена государством?
Решение
Рассуждения:
Из курса экономической теории мы знаем, что монополист, может производить любой объем продукции и продавать ее по цене, какой захочет. Главная цель монополиста – получить максимум прибыли при имеющихся возможностях.
Ценовая дискриминация – это продажа товара разным покупателям по разным ценам. Согласно закону спросу: чем выше цена, тем меньше реализуемый объем производства, или наоборот. Между тем от монополиста не зависит существующий на рынке спрос и уровень его издержек в данный момент времени.
Попробуем найти тот объем производства и соответственно уровень цен на каждом из двух рынков, максимизирующие прибыль монополиста при условии, что ценовая дискриминация незапрещена государством.
Действия:
А) Воспользуемся правилом максимизации прибыли монополиста при ценовой дискриминации:
MC = MR(1) = MR(2),
где 1, 2 – число разных групп покупателей, приобретающих монопольный товар по разным ценам.
Данное правило основано на принципе выравнивания предельных доходов, получаемых на каждом из двух рынков. Поскольку достигнутый при этом уровень доходов может быть выше или ниже предельных издержек, то для получения наибольшей массы прибыли необходимо или сокращать объём выпуска, или наращивать.
Первая производная общих издержек есть предельные издержки:
(TC)’ = MC = ½Q + 10.
Поскольку монополист функционирует на двух рынках,
то функция предельных издержек примет следующий вид:
MC = ½(Q(1) + Q(2)) + 10.
Выведим функции предельного дохода (MR(1) и MR(2)) монополиста на 2 рынках.
Функция предельного дохода есть первая производная общего дохода:
MR = (TR)’ = (P × Q)’.
Поскольку спрос на первом рынке составляет Q(1) = 400 – 2P(1),
а спрос на втором рынке равен Q(2) = 600 – 4P(2),
то обратные функции спроса, отражающие зависимость цены спроса от величины спроса соответственно примут соответствующий вид:
P(1) = 200 – ½ Q(1) и
P(2) = 150 – ¼ Q(2).
Отсюда функции предельного дохода на двух рынках составят:
MR(1) = (TR)’ = ((200 – ½ Q) × Q)’ = (200Q – ½ Q²)’ = 200 – Q(1);
MR(2) = (TR)’ = ((150 – ¼ Q) × Q)’ = (150Q – ¼ Q²)’ = 150 – ½Q(2).
Составим и решим систему уравнений:
Решим выражение (2) и подставим в первое (1). Получим:
Q(2) = 2Q(1) – 100.
Подставляем Q(2) в первое выражение и находим Q(1):
½(Q(1) + 2Q(1) – 100) + 10 = 200 – Q(1).
Следовательно, объем производства на каждом из двух рынков, максимизирующие прибыль монополиста составят:
• Q(1) = 96 штук;
• Q(2) = 92 штук.
Вычислим уровень цен на каждом из двух рынков, максимизирующий прибыль монополиста:
• P(1) = 200 – ½ × 96 = 152 д.е.
• P(2) = 150 – ¼ × 92 = 127 д.е.
Б) Подсчитаем прибыль монополиста при ценовой дискриминации по формуле:
PR = TR – TC.
• TR = (Q(1) × P(1) + Q(2) × P(2)) = (96 × 152 + 92 × 127) = 26 276 д.е.
• TC = ¼ (Q(1) + Q(2))² + 10(Q(1) + Q(2)) + 300 = (¼ × 188² + 10 × 188 + 300) = 11 016 д.е.
• PR = 15 260 д.е.
В) Как изменятся объём продаж, цены и прибыль, если ценовая дискриминация запрещена государством?
Во всех экономически развитых странах существует антимонополь-ное законодательство. Данные законы объявляют незаконными действия лиц, которые осуществляют дискриминацию в ценах между различными покупателями товаров одного и того же сорта, качества, когда результатами такой дискриминации является существенное ограничение конкуренции. Данный закон не налагает уголовной ответственности (т.е. является актом гражданского кодекса).
Если ценовая дискриминация будет запрещена государством, то товар на обоих рынках будет продаваться по одной и той же цене.
Отсюда общий рыночный спрос составит:
Q(D) = (400 – 2P(1)) + (600 – 4P(2)) = 1 000 – 6P.
Тогда обратная функция спроса примет следующий вид:
P = 167 – 1/6Q.
Определим объём производства, максимизирующий прибыль.
Найдём Q, исходя из условия максимизации прибыли MC = MR.
MC = ½Q + 10;
а MR = (TR)’ = ((167 - 1/6 Q) × Q)’ = (167 Q – 1/6 Q²)’ = 167 – 1/3 Q.
Приравняем значения MC и MR:
0,5Q + 10 = 167 – 1/3Q.
Следовательно, Q ≈ 188 шт., а Р ≈ 167 – 1/6 × 188 ≈ 136 д.е.
Найдем максимальное значение прибыли: PR = TR – TC.
PR = 188 × 136 – (¼ × 188² + 10 × 188 + 300) = 14 552 д.е.
Прирост прибыли монополиста при ценовой дискриминации составил:
708 д.е. (15260 – 14552).
|
|
| Задача №1.9.12
Объём спроса на продукцию предприятия выражается формулой:
QD = 200 – 4p, а объём предложения – QS = 6p – 100.
Величина переменных издержек на единицу продукции TVC = 25. Чему должна быть равна цена на единицу продукции p, чтобы прибыль П была максимальной?
Решение
В точке потребительского равновесия QS = QD, то есть
6p0 – 100 = 200 – 4p0,
откуда p0 = 30 (ден. ед.) – равновесная цена, à Q0 = 80 (ед.) – равновесный объём продукции.
Изобразим графически кривые спроса и предложения, и точку потребительского равновесия, находящуюся на их пересечении.
Рассмотрим три возможных варианта:
1) p > p0, à Q = QD, то есть П = QD * p – QD * TVC = QD(p – TVC),
подставим значения и получим:
П = (200 – 4p)*(p – 25) = –4p2 + 300p – 5000.
2) p = p0, à Q = QD = QS, à Qпродажи = Q0 = 80 (ед.), à
П2 = 80*(30 – 25) = 400 (ден. ед.).
3) p < p0, à Q = QS, то есть П = QS * p – QS * TVC = QS(p – TVC),
подставим значения:
П = (6p – 100)(p – 25) = 6p2 – 250p + 2500.
Далее случаи (1) и (3) можно решать аналитически, подставляя различные значения цены из интервала её значений или как-либо иначе, но гораздо проще выявить экстремумы прибыли через производную:
1) П = – 4p2 + 300p – 5000
П' = – 8p + 300;
– 8p + 300 = 0 à p = 75/2 = 37,5 (ден. ед.).
Значит, Q = QD = 200 – 4*37,5 = 200 – 150 = 50 (ед.), а
П1 = – 4p2 + 300p – 5000 = – 4*(37,5)2 + 300*37,5 – 5000 = 625 (ден. ед.).
2) Во втором случае прибыль была уже найдена: П2 = 400 (ден. ед.).
3) П = 6p2 – 250p + 2500
П' = 12p – 250;
12p – 250 =0 à p = 125/6 = 205/6 (ден. ед.).
Значит, Q = QS = 6*205/6 – 100 = 125 – 100 = 25 (ед.),
A П3 = 6p2 – 250p + 2500 = 6*(205/6)2 – 250*205/6 + 2500 = – 1041/6 (ден. ед.).
Можно заключить, что прибыль максимальна в первом случае, следовательно, цена единицы продукции должна равняться 37,5 денежным единицам.
|
|
Задача №1.9.13
На рынке монополистической конкуренции действует фирма, которая имеет функцию затрат ТС = Q3 – a × Q2+ 91 × Q.
Функция рыночного спроса Q = 75 – 2 × Р.
Определите, при каком значении переменной а данная фирма будет находиться в состоянии долгосрочного равновесия.
Какой уровень цены и объема выпуска она при этом установит?
Решение
Условие равновесия в долгосрочном периоде на рынке монополистической конкуренции:
AC = P,
а также общее для всех рыночных структур равенство предельных издержек и предельной выручки:
МС = MR.
Средние издержки фирмы определим по формуле:
 Обратная функция спроса имеет вид:
P = 37,5 – 0,5×Q
Найдём функцию предельных издержек как производную от общих издержек:
МС = (ТС)’= 3×Q2 – 2×a×Q + 91
И наконец, предельная выручка будет равна:
MR = (TR)’= (P×Q)’= (37,5×Q – 0,5×Q2)’= 37,5 – Q
Решим систему из двух уравнений:
Обратная функция спроса имеет вид:
P = 37,5 – 0,5×Q
Найдём функцию предельных издержек как производную от общих издержек:
МС = (ТС)’= 3×Q2 – 2×a×Q + 91
И наконец, предельная выручка будет равна:
MR = (TR)’= (P×Q)’= (37,5×Q – 0,5×Q2)’= 37,5 – Q
Решим систему из двух уравнений:
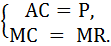
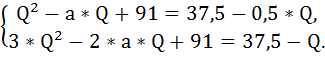 Умножим первое уравнение системы на 2 и вычтем из второго уравнения первое.
Умножим первое уравнение системы на 2 и вычтем из второго уравнения первое.
 Берём ответ с положительным знаком,
так как отрицательное значение Q экономического смысла не имеет.
Тогда переменная а будет равна:
а = 15,13
При этом установится цена:
P = 37,5 – 0,5 × 7,314 = 33,84
Итак, при а = 15,13 фирма будет находится в состоянии долгосрочного равновесия. При этом установиться цена Р = 33,84 и объём выпуска Q = 7,314.
Берём ответ с положительным знаком,
так как отрицательное значение Q экономического смысла не имеет.
Тогда переменная а будет равна:
а = 15,13
При этом установится цена:
P = 37,5 – 0,5 × 7,314 = 33,84
Итак, при а = 15,13 фирма будет находится в состоянии долгосрочного равновесия. При этом установиться цена Р = 33,84 и объём выпуска Q = 7,314.
|
|
Задача №1.9.14
Монополист, производящий табуретки, максимизирует прибыль.
Какую он назначит цену, если общие издержки составляют TC = 20 × Q + 100,
а эластичность спроса по цене постоянна и равна -2?
Решение
Условие максимизации прибыли на рынке монополии состоит в равенстве предельных издержек и предельного дохода в точке оптимального выпуска:
МС(Qопт) = МR(Qопт).
Предельный доход (или предельная выручка) определяется как:
частная производная общего дохода по количеству товара:
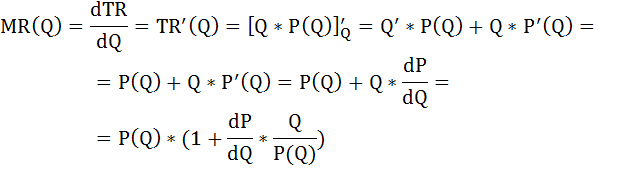 Напомним, что эластичность спроса по цене определяется по формуле:
Напомним, что эластичность спроса по цене определяется по формуле:
 Тогда подставив это выражение в формулу предельного дохода получим ещё одну формулу для расчёта предельного дохода и соответственно предельных издержек:
Тогда подставив это выражение в формулу предельного дохода получим ещё одну формулу для расчёта предельного дохода и соответственно предельных издержек:
 Таким образом, если известна эластичность спроса по цене и предельные издержки, то можно рассчитать ориентировочную цену продукта монополии.
Таким образом, если известна эластичность спроса по цене и предельные издержки, то можно рассчитать ориентировочную цену продукта монополии.
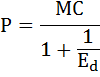 Предельные издержки легко найти, взяв производную от функции общих издержек:
МС = TC’ = (20 × Q + 100)’ = 20
Найдём монопольную цену.
Предельные издержки легко найти, взяв производную от функции общих издержек:
МС = TC’ = (20 × Q + 100)’ = 20
Найдём монопольную цену.
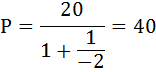
|
|
Задача №1.9.15
Известно, что в долгосрочном периоде средние переменные затраты монополистически конкурентной фирмы зависят от объема производства:
АVС = Q + 10.
Спрос на продукцию фирмы описывается формулой:
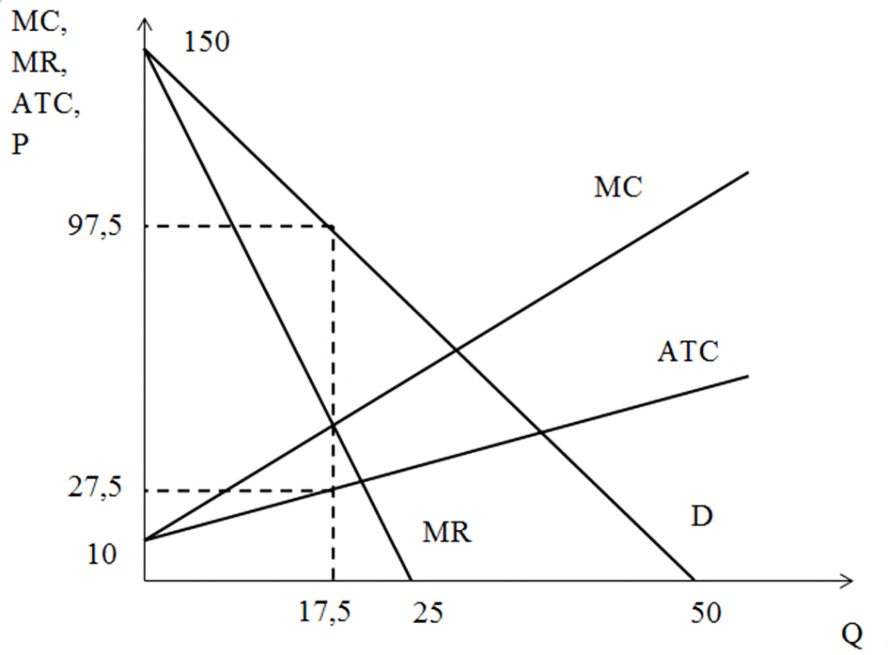
Р = 150 – 3Q.
Найдите параметры равновесия (цену и объем продаж) и сделайте вывод, находится фирма в состоянии долгосрочного или краткосрочного равновесия.
Нарисуйте график.
Решение
Найдём функцию переменных затрат:
VC = АVС × Q = (Q + 10) × Q = Q2 + 10 × Q
В долгосрочном периоде постоянные затраты равны нулю, следовательно, функция общих затрат будет иметь вид:
ТС = VC + FC = Q2 + 10 × Q
Соответственно функция средних общих затрат будет равна функции средних переменных затрат:
ATC = АVС = Q + 10
Предельные затраты фирмы на рынке определим как производную от функции общих затрат:
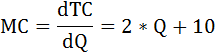 Выручка фирмы на рынке будет равна:
TR = P × Q = (150 – 3 × Q) × Q = 150 × Q – 3 × Q2
Найдём предельную выручку как производную от общей выручки:
Выручка фирмы на рынке будет равна:
TR = P × Q = (150 – 3 × Q) × Q = 150 × Q – 3 × Q2
Найдём предельную выручку как производную от общей выручки:
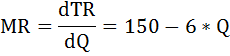 При равновесии в долгосрочном периоде в условиях монополистической конкуренции выполняются равенства:
P = ATC,
MC = MR.
Приравняем функцию предельных затрат к функции предельной выручки:
2Q + 10 = 150 – 6Q
Отсюда оптимальный объём выпуска фирмы равен:
Q = 17,5
Подставим это значение в равенство цены и средних общих издержек:
150 – 3 × 17,5 = 17,5 + 10
97,5 ≠ 27,5
P ≠ ATC
Следовательно, одно из условий равновесия долгосрочного периода не соблюдается, что свидетельствует о состоянии краткосрочного равновесия.
При равновесии в долгосрочном периоде в условиях монополистической конкуренции выполняются равенства:
P = ATC,
MC = MR.
Приравняем функцию предельных затрат к функции предельной выручки:
2Q + 10 = 150 – 6Q
Отсюда оптимальный объём выпуска фирмы равен:
Q = 17,5
Подставим это значение в равенство цены и средних общих издержек:
150 – 3 × 17,5 = 17,5 + 10
97,5 ≠ 27,5
P ≠ ATC
Следовательно, одно из условий равновесия долгосрочного периода не соблюдается, что свидетельствует о состоянии краткосрочного равновесия.
|
|
Задача №1.9.16
Из Л. Коломейцевой
Фирма работает в условиях монополии. Функции общих издержек и дохода фирмы представлены следующими уравнениями:
ТС = 25 + 2Q2;
ТR = 60 Q - Q2.
Определите объем производства, максимизирующий прибыль; средний и предельный доходы; средние и предельные издержки.
Построить и проанализировать графики.
На графике 1 начертить кривые общих издержек ТС, дохода TR и прибыли W.
На графике 2 – кривые среднего (AR) и предельного (MR) доходов; средних (АС) и предельных (МС) издержек.
На графике 3 построить кривые общих (ТС), общих постоянных (TFC), общих переменных (TVC) издержек и дохода (TR). Определите точку безубыточности.
На графике 4 отобразить кривые средних (АС), средних постоянных (AFC), средних переменных (AVC) и предельных (МС) издержек.
Анализируя графики, найдите:
- точку максимальной прибыли;
- область прибыли;
- «холм» доходов;
- границу эластичности;
- точку безубыточности.
|
|
Задача №1.9.17
Из Л. Коломейцевой
Фирма работает в условиях монополии. Функции общих издержек и дохода фирмы представлены следующими уравнениями:
ТС = 50 + 2Q2;
ТR = 40 Q - Q2.
Определите объем производства, максимизирующий прибыль; средний и предельный доходы; средние и предельные издержки.
Построить и проанализировать графики.
На графике 1 начертить кривые общих издержек ТС, дохода TR и прибыли W.
На графике 2 – кривые среднего (AR) и предельного (MR) доходов; средних (АС) и предельных (МС) издержек.
На графике 3 построить кривые общих (ТС), общих постоянных (TFC), общих переменных (TVC) издержек и дохода (TR). Определите точку безубыточности.
На графике 4 отобразить кривые средних (АС), средних постоянных (AFC), средних переменных (AVC) и предельных (МС) издержек.
Анализируя графики, найдите:
- точку максимальной прибыли;
- область прибыли;
- «холм» доходов;
- границу эластичности;
- точку безубыточности.
|
|
| Задача №1.9.18
Из Л. Коломейцевой
Предположим, что функции общих издержек фирмы и спроса продукции представлены следующими уравнениями:
ТС = 50 + 2Q + 0,5Q2;
Q = 12 – 0,5 P.
Определите объем производства, максимизирующий прибыль; средний и предельный доходы; средние и предельные издержки.
Построить и проанализировать графики.
На графике 1 начертить кривые общих издержек ТС, дохода TR и прибыли W.
На графике 2 – кривые среднего (AR) и предельного (MR) доходов; средних (АС) и предельных (МС) издержек.
На графике 3 построить кривые общих (ТС), общих постоянных (TFC), общих переменных (TVC) издержек и дохода (TR). Определите точку безубыточности.
На графике 4 отобразить кривые средних (АС), средних постоянных (AFC), средних переменных (AVC) и предельных (МС) издержек.
|
|
| Задача №1.9.19
Зависимость общих издержек конкурентной фирмы от объема выпуска описывается формулой ТС = X/3 + X²/48.
Известно, что средняя прибыль при оптимальном объеме выпуска равняется 1/6.
Найдите: 1) оптимальный объем производства и рыночную цену продукции фирмы;
2) общую прибыль фирмы при оптимальном объеме производства;
3) эластичность предложения по цене при оптимальном объеме производства.
Решение 1) Условие максимизации прибыли при совершенной конкуренции можно записать так: ТС’ = MC = P
TC’ = 1/3 + Х*/24
Также мы знаем, что
cредняя прибыль равна разности предельных и средних издержек:
π = МС – AС = 1/3 + Х*/24 – 1/3 – Х*/48 = 1/6
6Х* = 48
Х* = 8
Тогда P* = 1/3 + Х*/24 = 1/3 + 1/3 = 2/3
2) П = Р*·X* – TC = 16/3 – X*/3 – X*²/48 = 8/3 – 64/48 = 4/3
3) Условие максимизации прибыли – неявная функция предложения:
МС = Р = 1/3 + Х/24
24·Р = 8 + Х
ХП = 24·Р – 8
EP(XП) = X’П·P*/X* = 24·2/3·8 = 2
Ответ.Х* = 8, Р* = 2/3, П* = 4/3, EP(XП) = 2.
|
|
| Задача №1.10.1
Фирма сократила объём выпуска и продаж продукции. При этом выручка, постоянные издержки и средние переменные издержки не изменились.
Средние совокупные издержки выросли на 300 р./шт.
Первоначальная величина средних постоянных издержек составляла 1200 р./шт.
На сколько процентов подняла фирма цену на продукт?
Ответ: на 25%.
|
|
Задача №1.10.2
Сто фирм в условиях совершенной конкуренции имеют следующую зависимость общих издержек от объёма выпуска:
| Объём выпуска фирмы
|
|
|
|
| | Общие издержки фирмы, тыс. р.
|
| 45,5
| 51,6
| 58,2
|
Шкала рыночного спроса показана в следующей таблице:
| Величина рыночного спроса
| 80 000
| 90 000
| 100 000
| 110 000
| | Цена, р.
|
|
|
|
|
а) Определите рыночную цену.
б) Является ли производство прибыльным?
Какую экономическую прибыль (убыток) получает одна фирма?
Решение
а) В условиях совершенной конкуренции ни одна фирма не может повлиять на цену. Цена складываются под влиянием отраслевого спроса и отраслевого предложения. Найдём рыночное равновесие, при котором Qd = Qотр.
Рассчитаем объём выпуска всей отрасли, Qотр. = N*Qi, а также предельные издержки фирмы.
Для расчёта предельных издержек фирмы воспользуемся формулой:
МС = ΔTC / ΔQ,
Где: ΔTC – прирост общих издержек, ΔQ – прирост объёма выпуска.
Предельные затраты девятисотой единицы будут равны:
МС(900) = (45500 – 40000) / (900 – 800) = 55 и т. д.
Сведём исходные данные и результаты вычислений в одну таблицу:
| Объём выпуска фирмы, Qi
| Общие издержки фирмы, TC, р.
| Объём выпуска
отрасли, Qотр.
| Предельные издержки, МСi, р.
| Величина рыночного спроса, Qd
| Цена, Ррын р.
| |
| 40 000
| 80 000
| –
| 80 000
|
| |
| 45 500
| 90 000
|
| 90 000
|
| |
| 51 600
| 100 000
|
| 100 000
|
| |
| 58 200
| 110 000
|
| 110 000
|
|
Целью всех фирм является максимизация прибыли.
Условие максимизации прибыли: MR = MC.
В условиях совершенной конкуренции Р = MR.
Следовательно, условие максимизации прибыли для совершенного конкурента:
P = MC.
Из таблицы видно, что равновесие на рынке, при котором Qd = Qотр наступает при цене равной P = MC = 61 р.
Причём при такой цене каждая фирма произведёт 1000 единиц продукции.
б) Оптимальный объём выпуска, при котором прибыль будет максимальна, равен 1000 единиц.
Найдём прибыль при Q = 1000 по формуле:
П(1000) = TR – TC = PQ – TC = 61*1000 – 51 600 = 9 400
|
Поиск по сайту:
|
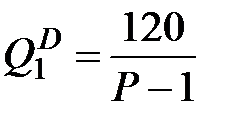 , а спрос второй группы равен
, а спрос второй группы равен 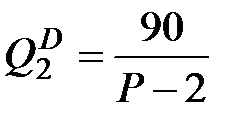 , где Р – цена снегоходов, которая по требованию правительства должна удовлетворять ограничению
, где Р – цена снегоходов, которая по требованию правительства должна удовлетворять ограничению 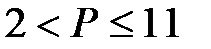 . Фирма способна произвести за неделю не более 60 снегоходов, причем издержки фирмы постоянны и равны TC = 200.
Определите максимальную прибыль, которую может получить фирма, если она не проводит ценовой дискриминации?
Решение
Обозначим выручку фирмы от продажи товара покупателям первой и второй группы через TR1 и TR2.
Из уравнений кривых спроса получим:
. Фирма способна произвести за неделю не более 60 снегоходов, причем издержки фирмы постоянны и равны TC = 200.
Определите максимальную прибыль, которую может получить фирма, если она не проводит ценовой дискриминации?
Решение
Обозначим выручку фирмы от продажи товара покупателям первой и второй группы через TR1 и TR2.
Из уравнений кривых спроса получим:  ;
;  .
Прибыль фирмы равна:
.
Прибыль фирмы равна: 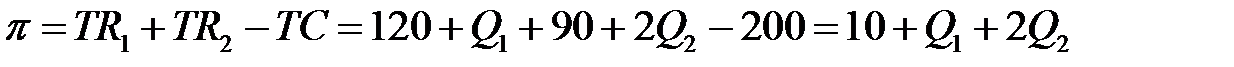 .
Если фирма не проводит ценовую дискриминацию, то задача максимизации прибыли сводится к нахождению такой цены, при которой
.
Если фирма не проводит ценовую дискриминацию, то задача максимизации прибыли сводится к нахождению такой цены, при которой  и выполняются ограничения
и выполняются ограничения  ,
,  ,
,  ,
, 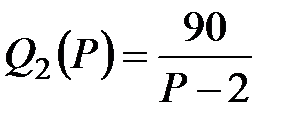 .
Поскольку функции спроса убывают с ростом цены на исследуемом интервале цен, то ограничение
.
Поскольку функции спроса убывают с ростом цены на исследуемом интервале цен, то ограничение  не может выполняться в оптимуме как строгое неравенство, т.к. иначе можно немного уменьшить цену, соответственно
не может выполняться в оптимуме как строгое неравенство, т.к. иначе можно немного уменьшить цену, соответственно 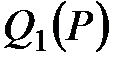 и
и 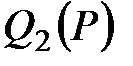 увеличатся и прибыль возрастет. Поэтому ищем оптимальное решение, предполагая равенство
увеличатся и прибыль возрастет. Поэтому ищем оптимальное решение, предполагая равенство 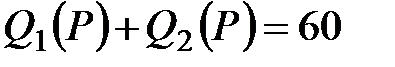 , т.е.
, т.е.  . Отсюда получаем квадратное уравнение
. Отсюда получаем квадратное уравнение  . Корни уравнения равны
. Корни уравнения равны  и
и 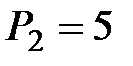 .
В необходимый интервал попадает второй корень, поэтому оптимальная цена
.
В необходимый интервал попадает второй корень, поэтому оптимальная цена  . При этом покупки покупателей первой и второй группы равны
. При этом покупки покупателей первой и второй группы равны  ,
,  , и фирма получает прибыль
, и фирма получает прибыль 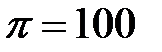 .
Ответ:
.
Ответ: 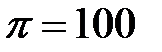 .
.
 Обратная функция спроса имеет вид:
P = 37,5 – 0,5×Q
Найдём функцию предельных издержек как производную от общих издержек:
МС = (ТС)’= 3×Q2 – 2×a×Q + 91
И наконец, предельная выручка будет равна:
MR = (TR)’= (P×Q)’= (37,5×Q – 0,5×Q2)’= 37,5 – Q
Решим систему из двух уравнений:
Обратная функция спроса имеет вид:
P = 37,5 – 0,5×Q
Найдём функцию предельных издержек как производную от общих издержек:
МС = (ТС)’= 3×Q2 – 2×a×Q + 91
И наконец, предельная выручка будет равна:
MR = (TR)’= (P×Q)’= (37,5×Q – 0,5×Q2)’= 37,5 – Q
Решим систему из двух уравнений:
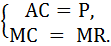
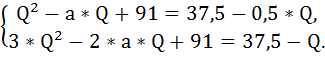 Умножим первое уравнение системы на 2 и вычтем из второго уравнения первое.
Умножим первое уравнение системы на 2 и вычтем из второго уравнения первое.
 Берём ответ с положительным знаком,
так как отрицательное значение Q экономического смысла не имеет.
Тогда переменная а будет равна:
а = 15,13
При этом установится цена:
P = 37,5 – 0,5 × 7,314 = 33,84
Итак, при а = 15,13 фирма будет находится в состоянии долгосрочного равновесия. При этом установиться цена Р = 33,84 и объём выпуска Q = 7,314.
Берём ответ с положительным знаком,
так как отрицательное значение Q экономического смысла не имеет.
Тогда переменная а будет равна:
а = 15,13
При этом установится цена:
P = 37,5 – 0,5 × 7,314 = 33,84
Итак, при а = 15,13 фирма будет находится в состоянии долгосрочного равновесия. При этом установиться цена Р = 33,84 и объём выпуска Q = 7,314.
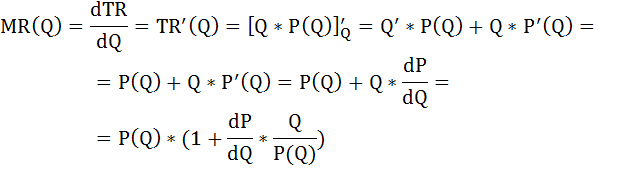 Напомним, что эластичность спроса по цене определяется по формуле:
Напомним, что эластичность спроса по цене определяется по формуле:
 Тогда подставив это выражение в формулу предельного дохода получим ещё одну формулу для расчёта предельного дохода и соответственно предельных издержек:
Тогда подставив это выражение в формулу предельного дохода получим ещё одну формулу для расчёта предельного дохода и соответственно предельных издержек:
 Таким образом, если известна эластичность спроса по цене и предельные издержки, то можно рассчитать ориентировочную цену продукта монополии.
Таким образом, если известна эластичность спроса по цене и предельные издержки, то можно рассчитать ориентировочную цену продукта монополии.
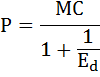 Предельные издержки легко найти, взяв производную от функции общих издержек:
МС = TC’ = (20 × Q + 100)’ = 20
Найдём монопольную цену.
Предельные издержки легко найти, взяв производную от функции общих издержек:
МС = TC’ = (20 × Q + 100)’ = 20
Найдём монопольную цену.
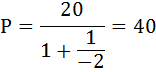
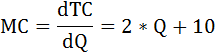 Выручка фирмы на рынке будет равна:
TR = P × Q = (150 – 3 × Q) × Q = 150 × Q – 3 × Q2
Найдём предельную выручку как производную от общей выручки:
Выручка фирмы на рынке будет равна:
TR = P × Q = (150 – 3 × Q) × Q = 150 × Q – 3 × Q2
Найдём предельную выручку как производную от общей выручки:
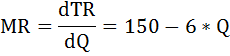 При равновесии в долгосрочном периоде в условиях монополистической конкуренции выполняются равенства:
P = ATC,
MC = MR.
Приравняем функцию предельных затрат к функции предельной выручки:
2Q + 10 = 150 – 6Q
Отсюда оптимальный объём выпуска фирмы равен:
Q = 17,5
Подставим это значение в равенство цены и средних общих издержек:
150 – 3 × 17,5 = 17,5 + 10
97,5 ≠ 27,5
P ≠ ATC
Следовательно, одно из условий равновесия долгосрочного периода не соблюдается, что свидетельствует о состоянии краткосрочного равновесия.
При равновесии в долгосрочном периоде в условиях монополистической конкуренции выполняются равенства:
P = ATC,
MC = MR.
Приравняем функцию предельных затрат к функции предельной выручки:
2Q + 10 = 150 – 6Q
Отсюда оптимальный объём выпуска фирмы равен:
Q = 17,5
Подставим это значение в равенство цены и средних общих издержек:
150 – 3 × 17,5 = 17,5 + 10
97,5 ≠ 27,5
P ≠ ATC
Следовательно, одно из условий равновесия долгосрочного периода не соблюдается, что свидетельствует о состоянии краткосрочного равновесия.