N2 (г) + 3H2 (г)↔ 2NH3 (г)
Константы равновесия могут быть записаны следующим образом:
Р2 (NH3) [NH3]2
Kp= -------------- Кс = -------------
P(N2)∙P3(H2) [N2]∙[H2]3
Связь между константами равновесия, выраженными через величины парциального давления и равновесных концентраций реагентов и продуктов реакции, отражена в формуле:
Кр = Кс∙(RT) ∆ν
где ∆ν =Σ νпрод. - Σ νисх.
В случае гетерогенных реакций в выражение константы химического равновесия входят парциальные давления (или концентрации) только газообразных участников реакции. Парциальные давления и концентрации веществ в твердом и жидком состояниях принимаются за единицу, так как их химические потенциалы равны. Например, для реакции
С (тв.) + О2 (г.)↔ СО2 (г.)
V→ =k∙[O2] V← = k∙[CO2]
[CO2]
Kc = ---------
[O2]
Для выражения константы равновесия (Ка) обратимых реакций растворов электролитов, значения равновесных концентраций заменяют на равновесные активности:
aCc ∙ aDd
Ка= ------------
aAa ∙ aBb
где а = С(х)∙γ, γ – коэффициент активности
(для реакции aA + bB↔ cC +dD)
Значение константы равновесия определяет положение равновесия, т.е. относительное содержание исходных веществ и конечных продуктов реакции, находящейся в состоянии равновесия.
Если Кс> 1,то в системе выше содержание конечных продуктов реакции, т.е. положение равновесия смещено в сторону прямой реакции.
Если Кс< 1, то в системе выше содержание исходных веществ, т.е. положение равновесия смещено в сторону обратной реакции.
Величина изменения свободной энергии Гиббса (∆G°) связана с константой равновесия обратимой реакции уравнением, выведенным Вант Гоффом в 1885 г. Он доказал, что между константой равновесия и энергией Гиббса обратимой реакции существует логарифмическая зависимость:
∆Gр. = - R∙T∙ln Kc,
где R – универсальная газовая постоянная, Т – температура (К).
Для упрощения математических расчетов зависимость константы равновесия и энергии Гиббса записать следующим образом:
∆Gр. = - 2,303∙R∙T∙lg Kc
Это уравнение дает возможность, зная ∆G, вычислить константу равновесия, и, наоборот, по экспериментально найденному значению константы равновесия рассчитать ∆G реакции.
Пользуясь уравнением изотермы химической реакции:
[C]c∙[D]d
∆G = ∆G° + RTln ----------
[A]a∙[B]b
(для реакции aA + bB↔ cC +dD)
можно определить, в каком направлении и до какого предела может протекать реакция в конкретных условиях при заданном составе исходных реагентов и продуктов реакции. Это же уравнение позволяет определить, какими должны быть условия реакции и состав исходной смеси, чтобы реакция протекала в нужном направлении и до рассчитанного предела.
Константы равновесия обратимых реакций зависят от температуры и природы реагирующих веществ, но не зависят от концентрации (Кс), активности (Ка), давления (Кр) реагирующих веществ.
Таким образом, в случае протекания обратимых реакций система самопроизвольно приходит к состоянию химического равновесия, из которого она без внешнего воздействия не может выйти, поскольку это требует увеличения энергии Гиббса.
Влияние изменения условий на химическое равновесие определяется принципом Ле Шателье:
Если на систему, находящуюся в состоянии химического равновесия, оказывать воздействие путем изменения концентрации реагентов, давления и температуры в системе, то равновесие всегда смещается в направлении той реакции, протекание которой ослабляет это воздействие.
Влияние изменения концентрации реагентов. В соответствии с принципом Ле Шателье введение в равновесную систему дополнительных количеств какого-либо реагента вызывает сдвиг равновесия в том направлении, при котором его концентрация уменьшается. Поэтому избыток исходного вещества (исходных веществ) вызывает смещение равновесия вправо, увеличивая степень превращения других реагентов; добавление продукта (продуктов) реакции вызывает смещение равновесия влево, т.е. уменьшение степени полноты ее протекания. Так, избыток кислорода увеличивает степень превращения SO2 в SO3 при контактном получении триоксида серы – возрастание концентрации молекул веществ ускоряет ту реакцию, которая их израсходует. В целях повышения выхода продуктов реакции, во многих случаях смещение равновесия в сторону продуктов взаимодействия можно осуществить и их удалением из реакционной зоны, связывая их в малодиссоциирующие, труднорастворимые или нелетучие вещества. Так, введение в равновесную систему:
СН3СООН + СН3ОН ↔ СН3СООСН3 + Н2О
водоотнимающих веществ (например, Н2SO4) позволяет сместить равновесие этой реакции вправо, т.е. в сторону образования продуктов реакции.
Таким образом, при изменении в равновесной системе концентрации любого из реагентов, исходное соотношение концентраций реагентов и величина константы равновесия в состоянии последующего равновесия не изменятся, хотя положение равновесия сместится в ту или иную сторону.
Влияние изменения давления в системе. Давление не изменяет величины константы равновесия обратимой реакции, так как она зависит только от температуры и природы реагирующих веществ, следовательно, с давлением меняется ∆G реакции.
Повышение давления в системе смещает химическое равновесие в направлении реакции, идущей с образованием меньшего числа молей газообразных веществ, т.е. в сторону уменьшения объема, а понижение давления в системе вызывает сдвиг равновесия в противоположную сторону. При равном числе молей газообразных исходных веществ и продуктов реакции изменение давления не смещает химическое равновесие. Влияние давления на химическое равновесие при Т = const показано схемой, где в первом случае рассмотрена реакция, сопровождающаяся уменьшением объема; а во втором – реакция, сопровождающаяся увеличением объема.
Чем меньше абсолютное значение изменения объема в системе, тем меньше влияние давления на равновесие. Поэтому при небольших значениях давления оно не влияет на равновесие системы. В гетерогенных процессах объемом конденсированной фазы можно пренебречь, однако, при сверхвысоких давлениях объем газов становится соизмеримым с объемом твердых тел и жидкостей. Если рассматривать реакции, в которых среди реагентов нет газообразных продуктов, например, процесс модификационного превращения С(графит)→С(алмаз), так как в данном случае изменение объема ничтожно мало, то даже для незначительного сдвига равновесия вправо требуется весьма значительное изменение (повышение) давления.
Для точного учета влияния давления на равновесие реакций, особенно при высоких давлениях, следует принимать во внимание изменение величины объема с давлением; так, если по мере повышения давления абсолютное значение изменения объема уменьшается, то будет уменьшаться и эффект действия давления в системе.
Влияние изменения температуры в системе. В соответствии с принципом Ле Шателье нагревание вызывает смещение равновесия в сторону того из двух встречных процессов, протекание которого сопровождается поглощением теплоты, т.е. в сторону эндотермической реакции. Понижение температуры приводит к противоположному эффекту: равновесие смещается в сторону того процесса, протекание которого сопровождается выделением тепла, в сторону экзотермической реакции.Из этого следует, что для суждения о влиянии температуры необходимо знать тепловой эффект изучаемого процесса. Как уже говорилось ранее, тепловой эффект реакции может быть определен опытным путем или по закону Гесса. Направление смещения и его степень определяются знаком и величиной теплового эффекта; чем больше ∆Н, тем значительнее влияние температуры; наоборот, если ∆Н близко к нулю, то и температура практически не влияет на равновесие. На схеме отражено влияние температуры на химическое равновесие при р = const, где первая зависимость приведена для эндотермической реакции, вторая – для экзотермической реакции. Законы наступления, сохранения и смещения динамического равновесия справедливы не только для химических и физико-химических процессов, но и имеют аналоги в живой природе. Соблюдение этого принципа в живых системах позволяет им поддерживать состояние гомеостаза. Основу гомеостаза составляет стационарное состояние системы, причем далекое от равновесия, из-за чего живые системы способны к эволюции.
Основы биоэнергетики.
Протекание жизненных процессов требует затрат энергии. Источником энергии для живых организмов служит пища. Главными компонентами пищи являются жиры, белки и углеводы, окисление которых сопровождается выделением энергии. В медицине энергетическую характеристику продуктов питания принято считать в калориях. Поскольку пища – разнородная смесь, ее калорийность, как правило, приводят в виде средних значений на 100 г.
Калорийностью питательных веществ – называется энергия, выделяемая при полном окислении (сгорании)1 г. питательных веществ.
Взаимосвязь между единицами энергии выражается соответствием:
1 калория = 4.18 Дж
Хорошо известная всем калорийность пищевых продуктов – не что иное, как теплота их сгорания, которую можно измерить экспериментально.
Начало таким измерениям положили Антуан Лавуазье и Пьер Симон в 1780 г. Определяя при помощи калориметра количество теплоты, выделенное морской свинкой, они установили, что окисление пищи в организме и вне его, дает близкие тепловые эффекты. На основании этих опытов был сделан важный вывод: живой организм выделяет теплоту за счет окисления в нем пищи кислородом воздуха. Это позволило объяснить различие в цвете артериальной и венозной крови, а в дальнейшем послужило исходным пунктом к открытию первого закона термодинамики.
Конечно, окисление питательных веществ в организме протекает совсем не так, как в калориметре. Это сложные многостадийные процессы с участием биологических катализаторов (ферментов). Однако, согласно закону Гесса, теплота, выделяемая при окислении питательных веществ, не зависит от того, окисляется она в организме или в калориметре, если продукты ее окисления одинаковы. Наибольшую энергетическую ценность имеют жиры, при окислении которых выделяется 37.7 –39.8 кДж/г (9.3 ккал/г). В процессе усвоения углеводов в организме человека выделяется 16.5 –17.2 кДж/г (4.1 ккал/г). На этом же уровне находится и калорийность белков.
Информация о выделении теплоты очень важна для понимания путей преобразования различных веществ в энергию в живых организмах.
В основе научной диетологии лежит соответствие калорийности пищевого рациона энергозатратам человека. Биоэнергетику организма можно регулировать не только с помощью выбора отдельных продуктов, но, главным образом, их сочетанием.
Зная основные термодинамические закономерности, химический состав продуктов питания и энергетические характеристики питательных веществ, врач должен уметь с учетом суточной потребности человека в энергии и на основе энергетического баланса его жизнедеятельности составить оптимальный рацион питания (энергоменю).
Л А Б О Р А Т О Р Н А Я Р А Б О Т А.
Количество теплоты измеряют по ее переносу от одного тела к другому. Повышение температуры тела определяется теплоемкостью:
С = Q/∆T,
Где С – теплоемкость, Q – количество теплоты, полученной телом, ∆Т – изменение температуры тела.
Соответственно, зная теплоемкость и изменение температуры, можно рассчитать количество теплоты, полученное или выделенное телом.
Тепловые эффекты реакций измеряют с помощью специальных приборов – калориметров. Этот термин предложили в 1780 г. французские ученые Антуан Лоран Лавуазье и Пьер Симон Лаплас. Основоположником калориметрии считается английский химик Джозеф Блэк, известный своими работами о природе теплоты.
Простейший калориметр – теплоизолированный сосуд с водой, снабженный мешалкой и термометром. Контейнер, в котором протекает исследуемый процесс (например, химическая реакция), помещают в калориметр и регистрируют изменение температуры воды. Зная теплоемкость калориметра, рассчитывают количество выделившейся теплоты. На рисунке представлена схема строения пламенного калориметра:
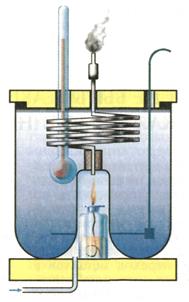
ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ ТЕПЛОВЫХ ЭФФЕКТОВ.
Определение тепловых эффектов химических процессов является задачей термохимии. Термохимические методы имеют большое значение не только в химических, но и в медико-биологических науках. Энергия, необходимая живым организмам для совершения работы, поддержания постоянной температуры тела и т.д., получается организмом за счет экзотермических реакций окисления, протекающих в клетках.
В химических лабораториях применяется простейший калориметр, который состоит из сосуда для проведения химической реакции, помещенного во внешнюю оболочку. Калориметр снабжен термометром, мешалкой для быстрого достижения однородности раствора, и воронкой для введения в сосуд растворов реагирующих веществ. Количество теплоты, выделяющейся или поглощающейся в калориметре, определяют по общей теплоемкости всех частей калориметра и изменению температуры.
РАБОТА № 1. Определение теплоты реакции нейтрализации сильной кислоты сильным основанием.
Цель работы: научиться определять теплоту реакции нейтрализации сильной кислоты сильным основанием.
Теплотой нейтрализации называется количество теплоты, которое выделяется при взаимодействии грамм-эквивалента кислоты с грамм-эквивалентом основания. Нейтрализация 1 г-экв. сильной кислоты сильным основанием, в достаточно разбавленном растворе, сопровождается почти одинаковым экзотермическим тепловым эффектом, отвечающим одному и тому же процессу – образованием 1 моля жидкой воды из гидратированных ионов по уравнению:
 H+aq + OH-aq H2O(ж), Qнейт.=55.9 кДж/г-экв.
H+aq + OH-aq H2O(ж), Qнейт.=55.9 кДж/г-экв.
Постоянство теплоты нейтрализации не соблюдается при нейтрализации слабого основания сильной кислотой или наоборот, так как в этих реакциях на тепловой эффект реакции влияет теплота диссоциации слабого электролита.
Выполнение работы. Во взвешенный калориметрический стакан помещают 50 мл 1.0 N раствора щелочи и записывают показание термометра. В отдельный стакан отмеряют 60 мл 1.0 N раствора соляной кислоты и измеряют его температуру. Поместив мешалку и термометр в калориметрический стакан, его закрывают крышкой. Затем, при перемешивании, вливают через воронку раствор кислоты в калориметр и следят за показаниями термометра, отмечая самую высокую температуру.
Результаты опыта записывают в таблицу:
Таблица1. Результаты вычислений.
| Масса калориметрического стакана, m1, г. | |
| Концентрация растворов, моль/л | |
| Объем раствора щелочи, V1, мл | |
| Объем раствора кислоты, V2, мл | |
| Температура щелочи, tºщ. | |
| Температура кислоты, tºк. | |
| Начальная температура, tº1=0.5(tºщ.+ tºк.) | |
| Температура поле нейтрализации tº2 | |
| Общая масса растворов m2=ρ(V1+V2) |
Вычисления:
1. Вычисление теплоты, выделившейся в результате реакции, производят по формуле:
q=(m1∙c1+m2∙c2) ∙(t2 – t1)
Удельную теплоемкость стекла (с1) принять равной 0,753 Дж/г∙град., раствора (с2) – 4,184 Дж/г∙град., плотность раствора (ρ) – 1 г/мл.
2. Чтобы определить теплоту нейтрализации, необходимо пересчитать выделившуюся теплоту на 1 грамм-эквивалент щелочи, так как кислота взята в избытке.
Расчет производят по формуле:
Qнейтр. = q∙1000/Nщ.∙Vщ., Дж/г-экв.
3. Сравнивают опытное и теоретическое значения теплоты нейтрализации и определяют (в%) относительную ошибку опыта:
% ошибки =((Qтеор. – Qопыт.)/ Qтеор)∙100%
В отчете о работе следует кратко описать ход определения, внести результаты опыта и расчеты.
РАБОТА №2. Определение теплоты растворения соли.
Цель работы: Определить интегральную теплоту растворения хлорида калия. Определить теплоту растворения и гидратации безводного хлорида кальция.
Интегральной теплотой растворения называют количество теплоты, выделяемой или поглощаемой при растворении 1 моля вещества в определенном объеме растворителя.
Интегральная теплота растворения электролитов определяется исходя из двух стадий данного процесса: во-первых, поглощения теплоты, которая расходуется на разрушение кристаллической решетки (Q1), и, во-вторых, выделения теплоты вследствие гидратации или сольватации каждого иона молекулами растворителя (Q2).
Qраств.=-Q1 + Q2
Выполнение работы: Во взвешенный калориметрический стакан наливают 100 мл дистиллированной воды. Отвешивают около 2 г хорошо измельченного хлорида калия KCl с точностью до 0,01г. Записывают температуру воды в калориметре и затем, при перемешивании, через воронку прибавляют навеску соли. При растворении соли температура раствора понижается, в результаты опыта записывают ее минимальное значение.
Данные эксперимента записывают в таблицу2:
Таблица 2. Результаты вычислений.
| Масса калориметрического стакана, m1, г. | |
| Масса воды, m2, г. | |
| Навеска соли, m3, г. | |
| Температура воды, t1° | |
| Температура раствора соли,t2° |
Теплоту растворения рассчитывают, используя формулу:
Qраств.=((t2 – t1)∙c∙M)/m3
где с=c1∙m1 +c2∙m2, М – молярная масса соли.
Удельная теплоемкость стекла (с1) и раствора (с2) указана в работе №1. Интегральная теплота растворения хлорида калия
Qраств.=-17.577 кДж/моль
Таким же образом проводят опыт с безводным хлоридом кальция CaCl2. В калориметрический стакан наливают 50 мл дистиллированной воды, отвешивают около 2 г. хорошо измельченной соли с точностью до 0,01 г.
Определив теплоту растворения безводного хлорида кальция CaCl2, вычисляют теплоту гидратации этой соли, зная теплоту растворения кристаллогидрата CaCl2∙6H2O (Q2=19.08 кДж/моль).
Qгидр.=Q1 р.безв. – Q2 р. гидр.
В отчете о работе кратко опишите ход определения, внесите результаты и расчеты работы.
Примеры решения задач.
Задача №1. Вычислить теплоту гидратации безводной соли Na2SO4.
Решение. Гидратация солей протекает медленно и обычно приводит к образованию смеси кристаллогидратов. Теплоту гидратации можно вычислить, если известны теплоты растворения безводной соли и кристаллогидрата:
Na2SO4 + n Н2О→ 2Na+ + SO4 2- (раствор)+3.02 кДж
Na2SO4∙10 Н2О +m Н2О→ раствор Na2SO4 – 78.6 кДж,
Процесс растворения соли можно представить следующей схемой:
∆Нр.
 Na2SO4 + n Н2О 2Na+ + SO4 2- (раствор)
Na2SO4 + n Н2О 2Na+ + SO4 2- (раствор)


∆Н (гидр.) ∆Н (раств. крист.)
Na2SO4∙10 Н2О
По закону Гесса: ∆Нр =∆Н (гидр.) +∆Н (раств. крист.).
Тогда ∆Н (гидр.)= ∆Нр - ∆Н (раств. крист.) = 3.02 – (-78.6) = 81.62 кД/моль.
Задача № 2. Вычислить константу равновесия реакции:
NH3 + HCl ↔ NH4Cl (тв.)
Решение. Прежде всего, определим ∆Gр. реакции, используя следствие из закона Гесса. Находим по справочнику термодинамических величин значение ∆G веществ, входящих в уравнение реакции:
∆Gf° (NH3) = -16.7 кДж/моль, ∆Gf° (HCl) = -95.4 кДж/моль,
∆Gf °(NH4Cl) =-203.7 кДж/моль.
По следствию из закона Гесса: ∆G°p.f=∑νj∆G°j - ∑νi∆G°I
∆G°p.f = ∆Gf °(NH4Cl) –(∆Gf° (NH3) +∆Gf° (HCl)
∆G°p.f =-203.7 –(-16.7 + (-95.4)) = -91.6 кДж,
Теперь воспользуемся уравнением, связывающим ∆G и Кс реакции:
∆Gр. = - 2,303∙R∙T∙lg Kc
∆Gр.° = -2.303 ∙8.314∙298∙ lg Kc =-569∙lg Kc
-91.6 = -5.69∙ lg Kc
lg Kc ≈ 16, т.е. Kc = 1/[ NH3] ∙[HCl] =1016
Большое значение константы равновесия показывает, что при стандартной температуре равновесие реакции сильно смещено в сторону прямой реакции.
Задача № 3. Рассчитать будет ли протекать при 25°С реакция?
2NO2→ N2O4 + 57.9 кДж/моль
Решение: Согласно термохимическому уравнению реакции:
∆Нр.° = - 57.9 кДж/моль
Найдем по таблице термодинамических величин значения энтропии для веществ, входящих в реакцию, и рассчитаем значение энтропии реакции:
S°(NO2) =240.2 Дж/моль∙К, S°(N2O4) =304.0 Дж/моль∙К,
∆S°p.f=∑νjS°j - ∑νiS°i
∆S°p = S°(N2O4) – 2∙ S°(NO2) = 304.0 –2∙ 240.2 =-176.4 Дж/моль∙К
Найдем значение ∆Gр.° используя уравнение Гиббса:
∆G =∆Н - Т∆S
∆G°= -57900 – 298∙(-176.4) =-5323.8 Дж =-5.33 кДж
∆G< 0, однако, малость ее величины указывает, что реакция димеризации при 25°С практически не осуществима.
Задания для самостоятельного выполнения.
1. При сжигании 4.2 г. железа с серой выделилось 1.74 ккал. Рассчитайте энтальпию образования сульфида железа FeS.
2. Вычислите энтальпию образования фосфористого водорода PH3, если известно термохимическое уравнение реакции:
2PH3 + 4O2 = 3H2O + Р2О5 + 560.3 ккал
3. Теплота сгорания глюкозы равна 2816 кДж/моль; теплота сгорания этилового спирта равна 1236 кДж/моль. На основании этих данных вычислите тепловой эффект биохимического процесса брожения глюкозы:C6Н12О6 = 2С2Н5ОН(ж) + 2СО2(г)
4. Теплота растворения Na2SO3 равна 11.3 кДж/моль; теплота гидратации этой соли до Na2SO3∙7H2O составляет 58.1 кДж/моль. Вычислите теплоту растворения кристаллогидрата.
5. Рассчитайте изменение энтальпии, энтропии, и свободной энергии Гиббса для реакции окисления NO в NO2 в стандартных условиях.
А) Возможна ли эта реакция при 25°С?
Б) Какой фактор – энтальпийный или энтропийный определяет величину энергии Гиббса этой реакции?
6. Теплота сгорания углеводов и белков в организме человека составляет 4.1 ккал/г, жиров – 9.3 ккал/г. Среднесуточная потребность в белках, жирах, и углеводах для студентов мужчин составляет соответственно 113, 106, 451 г; для студентов женщин –96,90,363 г. Какова суточная потребность студентов в энергии?
Занятие 4.Строение атома. Химическая связь, ее свойства и методы описания.
Контрольные вопросы..
1. Основные законы квантовой механики. Квантование энергии. Корпускулярно – волновой дуализм. Принцип неопределённости.
2. Волновая функция. Атомная орбиталь. Вероятность и плотность вероятности.
3. Квантовые числа.
4. Периодический закон. Электронные структуры атомов.
5. Структура периодической системы. Периодичность свойств.
6. Порядок заполнения орбиталей. Принцип Паули. Правило Гунда. Принцип наименьшей энергии. Правило Клечковского.
7. Изображение электронной структуры атомов при помощи электронных формул и квантовых ячеек.
8. Химическая связь и строение молекул. Основные принципы взаимодействия атомов на примере молекулы водорода.
9. Основные типы химической связи.
10. Гибридизация.
11. Основные понятия метода валентных связей и метода молекулярных орбиталей.
Сложность структуры атома. Ядерная модель Э. Резерфорда
В основе атомно-молекулярной теории строения вещества лежит представление о возможности разделения физического тела на малые части, каждая из которых сохраняет химические свойства тела. Эти части были названы молекулами.
Предполагалось, что молекулы сложного состава можно разделить на части, называемые атомами. Атомы в химических реакциях не изменяются. Если допустить существование движущихся атомов и молекул, то можно объяснить многие наблюдаемые на опыте свойства физических тел. При этом считалось, что опытные факты можно истолковать, считая атомы и молекулы точечными телами. Однако в конце XIX – начале XX в. были открыты явления, заставляющие сделать предположение о сложности строения атомов и молекул.
Изучение прохождения электрического тока через газы и растворы позволило обнаружить одну из составных частей атома и молекулы – электрон.
При изучении прохождения электрического тока через растворы электролита были открыты законы электролиза и введено представление о существовании положительного и отрицательного заряженных атомов или групп атомов – катионов и анионов.
Эти факты привели к мысли о том, что атом можно представить как сложное образование, состоящее из электронов и области, несущей положительный заряд. Возник вопрос об относительном расположении электронов и положительно заряженной остальной части атома.
В 1904 году В. Томсон и Д. Д. Томсон предложили модель строения атома. Атом представляет положительно заряженный шар, в котором вкраплены отрицательно заряженные электроны.
В том же году японский физик Х. Нагаока предложил иную модель строения атома: атом имеет строение, напоминающее строение планеты Сатурн с её кольцами спутников. Основная часть атома - положительно заряженный шар, вокруг которого по кольцевым орбитам вращаются электроны.
В 1906 – 1911 гг. в лаборатории Э. Резерфорда было изучено прохождение через фольгу дважды ионизированных атомов гелия – α-частиц. Оказалось, что область положительного заряда атома очень невелика по размерам, что противоречило модели В. Томсона и Д. Д. Томсона. Э. Резерфорд использовал планетарную модель Х. Нагаоки. Однако он предложил в отличие от Нагаоки, что масса атома почти целиком сосредоточена в области положительного заряда. Эта область была названа ядром атома. Ядерная модель атома предложена Э. Резерфордом в 1911 г. Но она не могла объяснить факта устойчивости атома: ведь согласно законам электродинамики электроны должны были бы излучать электромагнитные волны, теряя кинетическую энергию и уменьшая свою скорость, пока не упадут на ядро.