Вопросы по экзамену
1. Основные задачи теории сооружений. Требования, предъявляемые к сооружениям. Понятие о расчётной схеме.
Строи́тельная меха́ника (теория сооружений) — совокупность наук о прочности, жёсткости и устойчивости строительных конструкций(сооружений).
Сооружение — это совокупность твердых тел, неподвижно соединенных между собой. Строительная механика обеспечивает строительство инженерных сооружений современными методами статического и динамического расчета.
Требования, предъявляемые к сооружениям:
1. прочность, жесткость и устойчивость;
2. экономичность;
3. неподвижность относительно основания и неизменность приданной геометрической формы в течение всего срока службы.
Задачами строительной механики являются определение внутренних усилий во всех элементах сооружений, изучение упругих перемещений, возникающих под действием внешней нагрузки, исследование устойчивости сооружений,а также установление законов образования наивыгоднейших форм сооружений.
Расчетная схема - это упрощенная, идеализированная схема, которая отражает наиболее существенные особенности объекта, определяющие его поведение под нагрузкой.
Расчет реальной конструкции начинается с выбора расчетной схемы. Выбор расчетной схемы начинается со схематизации свойств материала и характера деформирования твердого тела, затем выполняется схематизация геометрической формы реального объекта.
2.Основные предпосылки и гипотезы.
Гипотезы и допущения
Расчет реальных конструкций и их элементов является либо теоретически невозможным, либо практически неприемлемым по своей сложности. Поэтому в сопротивлении материалов применяется модель идеализированного деформируемого тела, включающая следующие допущения и упрощения:
|
|
Гипотеза сплошности и однородности: материал представляет собой однородную сплошную среду; свойства материала во всех точках тела одинаковы и не зависят от размеров тела.
Гипотеза об изотропности материала: физико-механические свойства материала одинаковы по всем направлениям.
Гипотеза об идеальной упругости материала: тело способно восстанавливать свою первоначальную форму и размеры после устранения причин, вызвавших его деформацию.
Гипотеза (допущение) о малости деформаций: деформации в точках тела считаются настолько малыми, что не оказывают существенного влияния на взаимное расположение нагрузок, приложенных к телу.
Допущение о справедливости закона Гука: перемещения точек конструкции в упругой стадии работы материала прямо пропорциональны силам, вызывающим эти перемещения.
Принцип независимости действия сил (принцип суперпозиции): результат воздействия нескольких внешних факторов равен сумме результатов воздействия каждого из них, прикладываемого в отдельности, и не зависит от последовательности их приложения.
Гипотеза Бернулли о плоских сечениях: поперечные сечения, плоские и нормальные к оси стержня до приложения к нему нагрузки, остаются плоскими и нормальными к его оси после деформации.
Принцип Сен-Венанна: в делениях, достаточно удалённых от мест приложения нагрузки, деформация тела не зависит от конкретного способа нагружения и определяется только статическим эквивалентом нагрузки.
|
|
Эти положения ограниченно применимы к решению конкретных задач. Например, для решения задач устойчивости утверждения 4-6 не справедливы, утверждение 3 справедливо не всегда.
3.Расчетная схема элемента сооружения. Классификация опор и элементов сооружений.
Расчётная схема сооружения — в строительной механике, упрощённое изображение сооружения, принимаемое для расчёта. Различают несколько видов расчётных схем, отличающихся основными гипотезами, положенными в основу расчёта, а также используемым при расчёте математическим аппаратом. Чем точнее расчётная схема соответствует действительному сооружению, тем более трудоёмок его расчёт.
Расчетные схемы сооружений можно классифицировать по-разному. Например, различают плоские и пространственные расчетные схемы, расчетные схемы по типу или способу соединения элементов, по направлению опорных реакций, по статическим и динамическим особенностям и т.д.
Сооружения опираются или закрепляются к основанию через какие-то опорные устройства. Взаимосвязь между сооружением и его основанием в расчетных схемах учитывается с помощью специальных знаков – опор. В пространственных и плоских расчетных схемах используются много типов опор. В плоских системах встречаются следующие типы опор (табл. 1.1).
Таблица 1.1. Основные типы опор плоских систем
Рассмотрим некоторые типы простых сооружений.
1. Балка – изгибаемый брус. Она бывает однопролетной или много-пролетной. Типы однопролетных балок: простая балка (рис. 1.5 а), консоль (рис. 1.5 б) и консольная балка (рис. 1.5 в). Многопролетные балки бывают разрезные (рис. 1.5 г), неразрезные (рис. 1.5 д) и составные (рис. 1.5 е):
|
|
Рис. 1.5
2. Рама – система прямых (ломаных или кривых) стержней. Ее стержни могут соединяться жестко или через шарнир. Вот некоторые типы рам: простая рама (рис. 1.6 а), составная рама (рис. 1.6 б), многоэтажная рама (рис. 1.6 в).
Рис. 1.6
3. Ферма – система стержней, соединенных шарнирами. Типов ферм много. Например, бывают стропильная ферма (рис. 1.7 а), мостовая ферма (рис. 1.7 б), крановая ферма (рис. 1.7 в), башенная ферма (рис. 1.7 г).
Рис. 1.7
4. Арка – система из кривых стержней. Некоторые типы арок: трехшарнирная (рис. 1.8 а), одношарнирная (рис. 1.8 б), бесшарнирная (рис. 1.7 в) арки.
Рис. 1.8
Существуют более сложные системы как комбинации простых систем. Они называются комбинированными системами. Например: арочная ферма (рис. 1.9 а), ферма с аркой (рис. 1.9 б), висячая система (рис. 1.9 в):
Рис. 1.9
По статическим особенностям различают статически определимые и статически неопределимые системы.
4.Классификация нагрузок.
В соответствии с 1 главой СНиП 2.01.07-85*-«НАГРУЗКИ И ВОЗДЕЙСТВИЯ» в зависимости от продолжительности действия нагрузок следует различать постоянные и временные (длительные, кратковременные, особые).
К постоянным нагрузкам относятся:
· Вес частей зданий и сооружений, в том числе вес несущих и ограждающих конструкций;
· Вес и давление грунтов(насыпей, засыпок), горное давление;
· Воздействие предварительного напряжения в конструкциях.
Из-за различного влияния на конструкции в зависимости от продолжительности действия временные нагрузки разделяют на длительные,
кратковременные и особые.
К временным длительным нагрузкам относятся:
· вес временных перегородок;
· вес стационарного оборудования, станков, аппаратов и др.
· нагрузки на перекрытиях в складских помещениях, холодильниках, зернохранилищах, архивах, библиотеках и подсобных зданиях и помещениях;
· нагрузки на перекрытия жилых и общественных зданий с пониженными нормативными значениями, приведенными в табл. 3 СНиП 2.01.07-85*;
· снеговые нагрузки с пониженным расчетным значением, определяемым умножением полного расчетного значения на коэффициент 0,5.
К остальным приведенным в СНиП 2.01.07-85* видам длительных нагрузок
при работе необходимо обратится на стр.2 СНиП 2.01.07-85*.
К кратковременные и особые.
К кратковременным нагрузкам относятся:
· нагрузки на перекрытия жилых и общественных зданий с полными
нормативными значениями;
· снеговые с полным расчетным значением;
· нагрузки от подвижного подъемно-транспортного оборудования (мостовых и подвесных кранов, тельферов, погрузчиков и т.п.);
· нагрузки, возникающие при изготовлении, перевозке и возведении конструкций, при монтаже и перестановке оборудования, а также нагрузки от веса временно с кратковременные нагрузки от веса насыпного грунта и др;
· нагрузки от оборудования, возникающие в пускоостановочном, переходном и испытательном режиме;
· ветровые нагрузки;
· температурные и климатические воздействия.
Более подробно кратковременные нагрузки описаны в СНиП 2.01.07-85*.
К особым нагрузкам относятся:
· сейсмические и взрывные воздействия;
· нагрузки, вызываемые резким нарушением технологического процесса, временной неисправностью или поломкой оборудования;
· воздействия неравномерных деформаций, сопровождающиеся изменением структуры грунта.
5. Основные понятия статики. Аксиомы статики и следствия из аксиом.
Ста́тика (от греч. στατός, «неподвижный») — раздел механики, в котором изучаются условия равновесия механических систем под действием приложенных к ним сил и моментов.
Основные понятия
Про тело говорят, что оно находится в равновесии, если оно покоится или движется равномерно и прямолинейно относительно выбранной инерциальной системы отсчёта.
В статике материальные тела считают абсолютно твёрдыми, т.к. изменение размеров тел обычно мало по сравнению с начальными размерами.
Связи
На тело влияют внешние силы, а также другие материальные тела, ограничивающие перемещение данного тела в пространстве. Такие тела называют связями. Сила, с которой связь действует на тело, ограничивая его перемещение, называется реакцией связи. Для записи условия равновесия системы связи убирают, а реакции связей заменяют на равные им силы.
Например, если тело закреплено на шарнире, то шарнир является связью. Реакцией связи при этом будет сила, проходящая через ось шарнира.
Системы сил
Если систему сил, действующих на твёрдое тело, можно заменить на другую систему сил, не изменяя механического состояния тела, то такие системы сил называются эквивалентными.
Для любой системы сил, приложенных к твёрдому телу, можно найти эквивалентную систему сил, состоящую из силы, приложенной в заданной точке (центре приведения), и пары сил. Эта сила называется главным вектором системы сил, а момент, создаваемый парой сил — главным моментом относительно выбранного центра приведения. Главный вектор равен векторной сумме всех сил системы и не зависит от выбранного центра приведения. Главный момент равен сумме моментов всех сил системы относительно центра приведения.
Аксиомы статики
Система сил, приложенная к телу или материальной точке, называется уравновешенной или эквивалентной нулю, если тело под действием этой системы находится в состоянии покоя или движется по инерции.
1.Не нарушая механического состояния тела, к нему можно приложить или отбросить уравновешенную систему сил.
2.О действии и противодействии. При всяком действии одного тела на другое со стороны другого тела имеется равное противодействие, такое же по величине, но противоположное по направлению.
3.О двух силах. Две силы, приложенные к одному и тому же телу, взаимно уравновешены (их действие эквивалентно нулю) тогда и только тогда, когда они равны по величине и действуют по одной прямой в противоположные стороны.
4.О равнодействующей. Равнодействующая двух сил, приложенных к одной точке, приложена к той же точке и равна диагонали параллелограмма, построенного на этих силах как сторонах.
5.Аксиома затвердевания. Если деформируемое тело находилось в равновесии, то оно будет находиться в равновесии и после его затвердевания.
6.Аксиома о связях. Механическое состояние системы не изменится, если освободить её от связей и приложить к точкам системы силы, равные действовавшим на них силам реакций связей.
6. Основные понятия статики. Момент силы. Момент пары.
Момент силы (синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — векторная физическая величина, равная векторному произведению радиус-вектора, проведённого от оси вращения к точке приложения силы, на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.
Пара сил. Момент пары сил
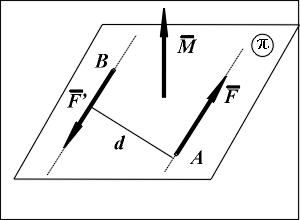Парой сил называется приложенная к твердому телу система двух сил (F,F'), равных по модулю, параллельных и направленных в противоположные стороны:
F = -F'; F=F'.
Расстояние d между линиями действия сил пары называется плечом пары; плоскость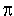 
, в которой действуют силы пары, называется плоскостью действия пары. Совокупность нескольких пар, действующих на тело, называется системой пар.
Пара сил не имеет равнодействующей. Она стремится сообщить телу некоторое вращение. Вращательный эффект пары характеризуется векторной величиной, называемой моментом пары. Момент пары сил относительно точки O
MO(F,F') = MO(F) + MO(F')
не зависит от выбора точки O и равен моменту одной из сил пары относительно точки приложения другой силы
M(F,F') = MA(F') = MB(F).
Момент пары сил M перпендикулярен плоскости действия пары, направлен по правилу правого винта и равен по модулю произведению модуля любой из сил на плечо пары: M = F · d.
Векторный момент пары сил может быть приложен в любой точке пространства, т.е. является свободным вектором.
Две пары сил, имеющие одинаковые векторные моменты, эквивалентны, т.е. оказывают на тело одинаковое механическое действие.
Эквивалентность пар: действие пары сил на твердое тело не изменится, если
- переместить пару в другое положение в плоскости ее действия;
- плоскость ее действия переместить параллельно самой себе;
- любым образом изменить модули сил и плечо пары, сохранив неизменным их произведение, т.е. момент пары M=F · d.
Сложение пар сил: система n пар сил с моментами M1,M2,...,Mn эквивалентна одной паре с моментом M, равным векторной сумме моментов этих пар: M = 
Mk.
Условие равновесия системы пар, приложенных к твердому телу: M = Mk=0.