Из двух сечений с одним и тем же полярным моментом сопротивления (или в случае некруглого сечения одним и тем же Wк), а следовательно, с одним и тем же допускаемым крутящим моментом, рациональным будет сечение с наименьшей площадью, т.е. обеспечивающее наименьший расход материала. Так как отношение Wp/A (или Wк/A) является величиной размерной, то для сравнения различных сечений удобно применять безразмерную величину
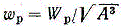
(при некруглом сечении 
), которую можно называть удельным моментом сопротивления при кручении. Чем больше 
, тем рациональнее сечение.
30. Внецентрическое сжатие коротких стержней. Внутренние усилия.
Внецентренное сжатие – это вид деформации, при котором продольная сила в поперечном сечении стержня приложена не в центре тяжести. При внецентренном сжатии, помимо продольной силы (N), возникают два изгибающих момента (Mx и My).
Рассмотрим, какие внутренние силы при внецентренном сжатии действуют на стержень в поперечном сечении. Пусть сжимающая сила (
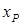) приложена в некоторой точке A с координатами 
и 
в главных центральных осях инерции x и y (см. рис. 10.1, а).
С учетом допущения, что стержень обладает большой жёсткостью на изгиб: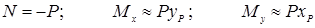 
.
Формула изгибающих моментов при внецентренном сжатии с учетом прогибов: 
, где 
и 
прогибы рассматриваемого поперечного сечения стержня в направлении осей 
и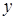 
, соответственно. Наше допущение о большой жесткости стержня на изгиб заключается в предположении: 
.
Нормальные напряжения в произвольной точке 
(см. рис. 10.1) с координатами и 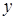будут равны: 
, где, согласно принципу независимости действия сил, первое слагаемое - напряжение от сжатия, а второе и третье – от изгиба.
Значения изгибающих моментов и координат исследуемой точки подставляются в формулу по абсолютному значению, а знак второго и третьего слагаемых определяется по физическому смыслу.
|
|
31. Внецентрическое сжатие коротких стержней. Нормальные напряжения. Условия прочности.
| Нормальные напряжения в поперечном сечении от действия силы Р смещенной относительно центра тяжести в точку А с координатами ХP и YP (рис. 7.2, а.б), определяются по формуле: |
|
| Р - равнодействующая внешних или внутренних сил; |
| F - площадь поперечного сечения; |
ХP, YP - координаты точки приложения силы Р. 
|
х, у - текущие координаты точки, в которой определяется напряжение  ;
|
| ix, iy - главные радиусы инерции поперечного сечения. |
| Рис. 7.2 |
| Квадраты главных радиусов инерции определяются по формулам: |
|
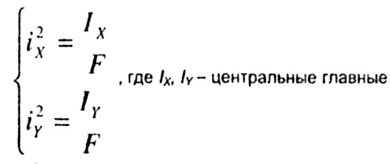
| моменты инерции поперечного сечения. Уравнение нулевой линии. |
|
| Так как Р # 0, то из этого выражения следует |
|
| Нулевая линия - прямая (Рис. 7.2, а). Точки пересечения нулевой линии с осями координат определяются выражениями: |
|
| Центром давления называют точку пересечения равнодействующей внешних или внутренних сил с плоскостью поперечного сечения. |
| (На рис. 7.2, а центр давления - точка А.) |
| При проектировании сооружений и различного рода опор из бетона, кирпичной кладки, чугуна и других материалов, плохо работающих на растяжение, основное требование - отсутствие растягивающих напряжений. Решение задачи опирается на свойство ядра сечения. |
| Ядром сечения называют часть плоскости поперечного сечения, расположенную в окрестности центра тяжести удовлетворяющую условию: если центр давления располагается внутри или на границе ядра сечения, то в любой точке поперечного сечения с текущими координатами (х, у) возникают напряжения одного знака. |
| Чтобы в поперечном сечении возникали напряжения одного знака, нулевая линия должна располагаться либо вне поперечного сечения, либо быть касательной к поперечному сечению, что используется при определении границ ядра сечения. |
Условия прочности при внецентренном растяжении-сжатии:
|
|
, 
.