| РАЦИОНАЛЬНЫЕ ФОРМЫПОПЕРЕЧНЫХ СЕЧЕНИЙ |
| Нормальные напряжения в произвольной точке поперечного сечения балки при прямом изгибе определяются по формуле: |
|
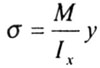
| где М - изгибающий момент в рассматриваемом поперечном сечении, |
| у - расстояние от рассматриваемой точки до главной центральной оси, перпендикулярной плоскости действия изгибающего момента, |
| lx - главный центральный момент инерции сечения. |
| Наибольшие растягивающие и сжимающие нормальные напряжения в данном поперечном сечении возникают в точках наиболее удаленных от нейтральной оси. |
| Их определяют по формулам: |
|
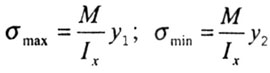
| где у1 и у2 расстояния от главной центральной оси х до наиболее удаленных растянутого и сжатого волокон. |
| Для балок из пластичных материалов, когда |
|
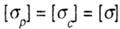
(где  - допускаемые напряжения для материала балки, соответственно на растяжение и сжатие), применяют сечения, симметричные относительно центральной оси.
|
| В этом случае условие прочности примет вид |
|
где  - момент сопротивления площади поперечного сечения балки относительно главной центральной оси:
|
|
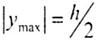
| h - высота сечения, |
| Мmax - наибольший по абсолютному значению изгибающий момент, |
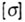 - допускаемое напряжение материала на изгиб.
|
| Кроме условия прочности балка должна удовлетворять и условию экономичности. |
| Наиболее экономичными являются такие формы поперечных сечений, для которых с наименьшей затратой материала (или при наименьшей площади поперечного сечения) получается наибольшая величина момента сопротивления. Чтобы форма сечения была рациональной, необходимо, по возможности распределять сечение подальше от главной центральной оси. |
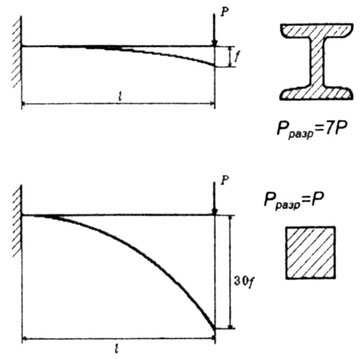
| Например двутавровая стандартная балка примерно в семь раз прочнее и в тридцать раз жестче, чем балка квадратного поперечного сечения той же площади, сделанная из того же материала (рис. 4.15). |
|
| Рис. 4.15 |
| Необходимо иметь в виду, что при изменении положения сечения по отношению к действующей нагрузке прочность балки существенно изменяется, хотя площадь сечения и остается неизменной. |
| В большинстве случаев с ростом момента инерции сечения возрастает и его момент сопротивления, но возможны и исключения, когда нерациональное увеличение момента инерции приводит к уменьшению момента сопротивления, т.е. снижению прочности бруса. |
| Для балок из хрупких материалов, различно сопротивляющихся растяжению и сжатию, расчетные формулы для подбора сечения имеют вид: |
|
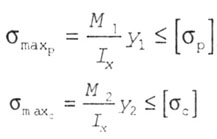
| где М1 и M2 - наибольшие по абсолютному значению изгибающие моменты в опасных сечениях соответственно для растянутых или сжатых волокон. |
| Для балок из хрупких материалов типа чугуна |
|
| следует применять сечения, несимметричные относительно нейтральной оси, например: тавровое, несимметричное двутавровое, П-образное (рис. 4.16). |
|
| При этом целесообразно располагать сечение таким образом, чтобы максимальные растягивающие и максимальные сжимающие напряжения в опасных сечениях балки были одновременно равны соответствующим допускаемым напряжениям. |
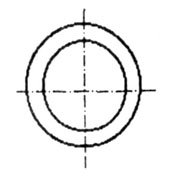
| Во всех предыдущих случаях нагрузка действовала на балку только в одном направлении, и форма поперечного сечения балки оптимизировалась, исходя именно из этого условия. В некоторых же инженерных и в большинстве естественных объектов нагрузка может действовать в различных направлениях. Приблизительно так распределяются нагрузки в фонарном столбе, ножке стула, бамбуке или кости ноги. В этих случаях надежнее ведут себя круглые полые трубы (рис. 4.17). |
| Однако существуют и другие способы увеличения прочности конструкции. Это предварительное напряжение. |
|
| Рис. 4.17 |
| Например дерево, которое подвергается изгибающим нагрузкам, вызванным давлением ветра. При сжатии древесина значительно хуже работает, чем при растяжении. Когда напряжение сжатия достигает 30 Мн/мг, дерево начинает ломаться. Стало известно, что ствол дерева оказывается напряженным. Каким-то образом дерево растет так, что внешние слои древесины обычно растянуты (примерно до 15 Мн/м), в то время как внутренние сжаты. Примерное распределение предварительных напряжений в сечении ствола показано на рис 4.18,6, напряжений только от изгиба - на рис. 4.18,а и суммарных напряжений - на рис. 4.18,в. |
|
| Рис. 4.18 |
| Дерево уменьшает наибольшую величину сжимающего напряжения примерно вдвое, правда, при этом возрастает максимальное растягивающее напряжение, но дерево вполне с ним может справиться. |
25. Плоский поперечный изгиб. Условие прочности. Подбор поперечного сечения балок.
Условия прочности при изгибе по нормальным и касательным напряжениям имеют вид
|
|
|
|
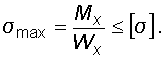
где Wх – осевой момент сопротивления;
.
Формула условия прочности при изгибе по нормальным напряжениям позволяет осуществитьподбор сечения балки при заданном материале и максимальном абсолютном значении изгибающего момента. Требуемый момент сопротивления балки при изгибе определяется из условия: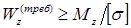 
.
|
|
При изменении положения сечения по отношению к действующей нагрузке прочность балки существенно изменяется, хотя площадь сечения и остается неизменной. Например, для балки прямоугольного поперечного сечения с отношением сторон 
, расположенной таким образом, что высота прямоугольника h перпендикулярна нейтральной оси x, прочнее той же самой балки повернутой на 
, в три раза, так как 
. В выражении дляосевого момента сопротивления балки прямоугольного поперечного сечения при изгибе в квадрате стоит тот ее размер, который перпендикулярен нейтральной оси. Следовательно, сечение балки необходимо располагать таким образом, чтобы силовая плоскость совпадала с той из главных центральных осей, относительно которой момент инерции минимален (ось, относительно которой главный момент инерции поперечного сечения максимален, является нейтральной осью). Это обстоятельство лишний раз подчеркивает важность темы «Определение положения главных центральных осей инерции поперечного сечения стержня».