23. Плоский поперечный изгиб. Посторение эпюр поперечных сил и изгибающих моментов.
Определение поперечных сил и изгибающих моментов - сечение 1
Отбросим правую часть балки и заменим ее действие на левую часть поперечной силой 
и изгибающим моментом 
. Для удобства вычисления закроем отбрасываемую правую часть балки листком бумаги, совмещая левый край листка с рассматриваемым сечением 1.
Поперечная сила в сечении 1 балки равна алгебраической сумме всех внешних сил, которые видим после закрытия
Видим только реакцию опоры, направленную вниз. Таким образом, поперечная сила равна:
кН.
Знак «минус» нами взят потому, что сила 
вращает видимую нами часть балки относительно первого сечения против хода часовой стрелки (или потому, что одинаково направлена с направлением поперечной силы по правилу знаков)
Изгибающий момент в сечении 1 балки, равен алгебраической сумме моментов всех усилий, которые мы видим после закрытия отброшенной части балки, относительно рассматриваемого сечения 1.
Видим два усилия: реакцию опоры и момент M. Однако у силы плечо практически равно нулю. Поэтомуизгибающий момент равен:
кН·м.
Здесь знак «плюс» нами взят потому, что внешний момент M изгибает видимую нами часть балки выпуклостью вниз. (или потому, что противоположно направлен направлению изгибающего момента по правилу знаков)
Определение поперечных сил и изгибающих моментов - сечение 2
В отличие от первого сечения, у силы реакции появилось плечо, равное а.
поперечная сила:
кН;
изгибающий момент:
кН·м.
Определение поперечных сил и изгибающих моментов - сечение 3
поперечная сила:
кН;
изгибающий момент:
кН ·м.
Определение поперечных сил и изгибающих моментов - сечение 4
Теперь удобнее закрывать листком левую часть балки.
поперечная сила:
кН;
изгибающий момент:
кН ·м.
Определение поперечных сил и изгибающих моментов - сечение 5
поперечная сила:
кН;
изгибающий момент:
кН ·м.
Определение поперечных сил и изгибающих моментов - сечение 1
поперечная сила и изгибающий момент:
.
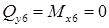По найденным значениям производим построение эпюры поперечных сил 
(рис. 7.7, б) и изгибающих моментов 
(рис. 7.7, в).
КОНТРОЛЬ ПРАВИЛЬНОСТИ ПОСТРОЕНИЯ ЭПЮР
Убедимся в правильности построения эпюр по внешним признакам, пользуясь правилами построения эпюр.
Проверка эпюры поперечных сил
Убеждаемся: под незагруженными участками эпюра поперечных сил идет параллельно оси балки, а под распределенной нагрузкой q – по наклоненной вниз прямой. На эпюре продольной силы три скачка: под реакцией – вниз на 15 кН, под силой P – вниз на 20 кН и под реакцией 
– вверх на 75 кН.
Проверка эпюры изгибающих моментов
На эпюре изгибающих моментов видим изломы под сосредоточенной силой P и под опорными реакциями. Углы изломов направлены навстречу этим силам. Под распределенной нагрузкой q эпюра изгибающих моментов изменяется по квадратичной параболе, выпуклость которой направлена навстречу нагрузке. В сечении 6 на эпюре изгибающего момента – экстремум, поскольку эпюра поперечной силы в этом месте проходит через нулевое значение.