Условие прочности при растяжении-сжатии

max = | | [ ]

15. Центральное растяжение и сжатие. Условие прочности. Три типа задач при центральном растяжении (сжатии).

Условие прочности позволяет решать три типа задач:

1. Проверка прочности (проверочный расчет)

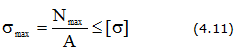
2. Подбор сечения (проектировочный расчет)

3. Определение грузоподъемности (допускаемой нагрузки)

16. Учёт собственного веса при центральном растяжении сжатии. Понятие о предельной длине.
Учет собственного веса при растяжении (сжатии)

Деформации при центральном растяжении и сжатии. Закон Гука.

Зако́н Гу́ка — утверждение, согласно которому деформация, возникающая в упругом теле (пружине, стержне, консоли, балке и т. п.), пропорциональна приложенной к этому телу силе.

При деформации тела возникает сила, которая стремится восстановить прежние размеры и форму тела. Эта сила возникает вследствие электромагнитного взаимодействия между атомами и молекулами вещества. Ее называют силой упругости.

Простейшим видом деформации являются деформации растяжения и сжатия. При малых деформациях (|x| << l) сила упругости пропорциональна деформации тела и направлена в сторону, противоположную направлению перемещения частиц тела при деформации:

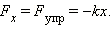
Это соотношение выражает экспериментально установленный закон Гука. Коэффициент k называется жесткостью тела. В системе СИ жесткость измеряется в ньютонах на метр (Н/м).

Коэффициент Пуассона.

Коэффициент Пуассона (коэффициент поперечной деформации) - показывает зависимость между продольными и поперечными деформациями элемента, характеризует упругие свойства материала.

Обозначается строчными греческими буквами ν или μ и является безразмерной величиной.

Определяется отношением относительных поперечных ε _поп и продольных ε _пр деформаций бруса (элемента):

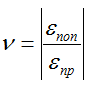
19 .Эксперементальные исследования механических свойств материалов. Диаграмма растяжения стали.

Диаграмма растяжения показывает зависимость удлинения образца от продольной растягивающей силы.

Ее построение является промежуточным этапом в процессе определения механических характеристик материалов (в основном металлов).

Диаграмму растяжения материалов получают экспериментально, при испытаниях образцов на растяжение.

Для этого образцы стандартных размеров закрепляют в специальных испытательных машинах (например УММ-20 или МИ-40КУ) и растягивают до их полного разрушения (разрыва). При этом специальные приборы фиксируют зависимость абсолютного удлинения образца от прикладываемой к нему продольной растягивающей нагрузки и самописец вычерчивает кривую характерную для данного материала.

На рис. 1 показана диаграмма для малоуглеродистой стали. Она построена в системе координат F-Δl, где:

F - продольная растягивающая сила, [Н];

Δl - абсолютное удлинение рабочей части образца, [мм]

Рис. 1 Диаграмма растяжения стального образца

Как видно из рисунка, диаграмма имеет четыре характерных участка:

I - участок пропорциональности;

II - участок текучести;

III - участок самоупрочнения;

IV - участок разрушения.

20 .Эксперементальные исследования механических свойств материалов. Повторные нагрузки и разгрузки. Явление наклепа.

Наклепом называют процесс повышения прочности и изменения упругих свойств металлических элементов путем пластического деформирования.

Если при испытании на растяжение стальной образец разгрузить не доводя до разрушения (точка М на рис.1), то в процессе разгрузки зависимость между силой F и удлинением Δl изобразится прямой MN. Опыт показывает, что эта прямая параллельна прямой ОА. При разгрузке деформация полностью не исчезает. Она уменьшается на величину упругой части удлинения (отрезок равный Δl_у).

Отрезок ОN диаграммы растяжения представляет собой остаточное удлинение (отрезок равный Δl_ост). Его называют также пластическим удлинением, а соответствующую ему деформацию – пластической деформацией. Таким образом,

Δl = Δl_у + Δl_ост

Соответственно

ε = ε_у + ε_ост

Если образец был нагружен в пределах участка ОА и затем разгружен, то удлинение будет чисто упругим, и Δl_ост=0.

Рис. 1

При повторном нагружении образца диаграмма возвращается по прямой NM и далее проходит по кривой MDE (рис. 1) так, как будто промежуточной разгрузки и не было.

Следовательно, при повторных нагружениях образца, предварительно растянутого до возникновения в нём напряжений, больше предела текучести, предел пропорциональности повышается до того уровня, которого достигли напряжения при предшествующей нагрузке. Если между разгрузкой и повторным нагружением был перерыв, то предел пропорциональности повышается ещё больше.

Следует отметить, что диаграмма NMDE, получаемая при повторном нагружении, не имеет площадки текучести, поэтому для образца, претерпевшего разгрузку и повторное нагружение, определяется условный предел текучести (σ_0.2),который, очевидно, выше предела текучести при первичном нагружении.

Явление повышения предела пропорциональности и снижения пластичности материала при повторных нагружениях называется наклёпом.

Наклёп во многих случаях является нежелательным явлением, так как наклёпанный материал становится более хрупким. Поэтому наклёп часто снимают отжигом – нагревом до определённой температуры.

В целом ряде случаев наклёп полезен и его создают искусственно, например, в деталях подвергающихся воздействию переменных нагрузок и при производстве арматуры.