Условия равновесия системы сходящихся сил

(F₁, F₂,...,F_n)~R => для равновесия тела, находящегося под действием системы сходящихся сил, необходимо и достаточно, чтобы их равнодействующая равнялась нулю: R = 0. Следовательно, в силовом многоугольнике уравновешенной системы сходящихся сил конец последней силы должен совпадать с началом первой силы; в этом случае говорят, что силовой многоугольник замк­нут (рис. 2.3). Это условие исполь­зуется при графическом решении задач для плоских систем сил. Векторное равенство R=0 эквивалентно трем скалярным равен­ствам: R_x=åF_kx=F_1x+F_2x+…+F_nx=0; R_y=åF_ky=F_1y+F_2y+…+F_ny=0; R_z=åF_kz=F_1z+F_2z+…+F_nz=0; где F_kx, F_ky, F_kz– проекции силы F_k на оси, а R_x, R_y, R_z– проекции равнодействующей на те же оси. Т. е. для равновесия сходящейся системы сил необходимо и достаточно равенства нулю алгебраических сумм проекций всех сил данной си­стемы на каждую из координатных осей. Для плоской системы сил пропадает условие, связанное с осью Z. Условия равновесия позволяют проконтролировать, нахо­дится ли в равновесии заданная система сил.

8. Плоская система сил. Понятие о главном векторе и главном моменте плоской системы сил. Условия равновесия плоской системы сил.
Плоская система сил – система сил, расположенных в одной плоскости. Система сил приводится к одной силе – главному вектору и к паре сил, момент которой равен главному моменту. Момент пары сил направлен перпендикулярно к плоскости, в которой лежат силы. В плоских системах нет необходимости использовать векторное представление момента. Теорема Вариньона – если плоская система сил приводится к равнодействующей, то ее момент относительно какой-либо точки равен алгебраической (т.е. с учетом знака) сумме моментов всех сил относит. той же точки.
Главный вектор и главный момент плоской системы сил

Рассмотрим плоскую систему сил (F1, F2,..., Fn),действующих на твердое тело в координатной плоскости Oxy.

Главным вектором системы сил называется вектор R, равный векторной сумме этих сил:

R = F1 + F2 +... + Fn = Fi.

Для плоской системы сил ее главный вектор лежит в плоскости действия этих сил.

Главным моментом системы сил относительно центра O называется вектор LO, равный сумме векторных моментов этих сил относительно точки О:

LO = MO(F1) + MO(F2) +... + MO(Fn) = MO(Fi).

Вектор R не зависит от выбора центра О, а вектор LO при изменении положения центра О может в общем случае изменяться.

Для плоской системы сил вместо векторного главного момента используют понятие алгебраического главного момента. Алгебраическим главным моментом LO плоской системы сил относительно центра О, лежащего в плоскости действия сил, называют сумму алгебраических моментов этих сил относительно центра О.

Главный вектор и главный момент плоской системы сил обычно вычисляется аналитическими методами.
Уравнения равновесия плоской системы сил

Для равновесия произвольной плоской системы сил, действующих на твердое тело, необходимо и достаточно, чтобы сумма проекций всех сил на каждую из двух прямоугольных осей, расположенных в плоскости действия сил, были равны нулю и сумма алгебраических моментов сил относительно любой точки, расположенной в плоскости действия сил, также была равна нулю:

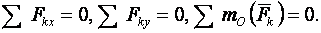(3.4)

Равенства (3.4) представляют так называемую основную форму условий равновесия при действии на тело плоской системы сил. Условия равновесия тела под действием плоской системы сил могут быть представлены еще в двух других формах.

Вторая форма условий равновесия:

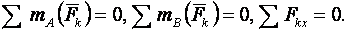(3.5)

т. е. должны быть равны нулю суммы моментов сил относительно любых двух точек А, В, расположенных в плоскости действия сил, и сумма проекций всех этих сил на ось х (при этом ось х не должна быть перпендикулярна прямой АВ).

Третья форма условий равновесия:

(3.6)

т. е. должны быть равны нулю суммы алгебраических моментов всех сил относительно любых трех точек А, В, С (эти точки расположены в плоскости действия сил и не лежат на одной прямой).

Если на объект действует плоская система параллельных сил, условия равновесия выражаются двумя формами уравнений равновесия:

(3.7)

или

(3.8)

В формулах (3.7) ось у следует выбирать параллельно силам, центр А выбирается произвольно. В формулах (3.8) отрезок АВ не должен быть параллелен силам.

Направления осей координат х и у следует выбирать так, чтобы они были перпендикулярны неизвестным силам.

За центр моментов следует выбирать точку пересечения двух неизвестных сил или точку на линии действия неизвестной силы.

Рациональный выбор формы уравнений равновесия, направления осей координат и центров моментов позволяет составлять такие уравнения равновесия, каждое из которых содержит по одной неизвестной. Решение такой системы уравнений сопровождается минимумом вычислений.

9. Определение опорных реакций в статически определимых балках и рамах.

10. Геометрические характеристики плоских сечений.
В расчетах конструкций на механическую надежность очень часто приходится оперировать такими характеристиками плоских фигур, как статический момент, осевой и полярный моменты инерции. Хотя вычисление вышеназванных геометрических характеристик относится к числу простейших задач интегрального исчисления, тем не менее, в силу их узкого прикладного значения они практически не рассматриваются во втузовском курсе высшей математики. По установившейся традиции геометрические характеристики плоских фигур изучаются в курсе сопротивления материалов.

Геометрические характеристики – числовые величины (параметры), определяющие размеры, форму, расположение поперечного сечения однородного по упругим свойствам деформируемого элемента конструкции (и, как следствие, характеризующие сопротивление элемента различным видам деформации).