Если при прямом или косом изгибе в поперечном сечении бруса действует только изгибающий момент, то соответственно имеется чистый прямой или чистый косой изгиб. Если в поперечном сечении действует также и поперечная сила, то имеется поперечный прямой или поперечный косой изгиб.
Если изгибающий момент 
является единственным внутренним силовым фактором, то такой изгиб называется чистым (рис.6.2). При наличии поперечной силы 
изгиб называется поперечным. Строго говоря, к простым видам сопротивления относится лишь чистый изгиб; поперечный изгиб относят к простым видам сопротивления условно, так как в большинстве случаев (для достаточно длинных балок) действием поперечной силы при расчетах на прочность можно пренебречь.
Смотрите условие прочности при плоском изгибе.
ри расчете балки на изгиб одной из важнейших является задача определения еепрочности. Плоский изгиб называется поперечным, если в поперечных сечениях балкивозникает два внутренних силовых фактора: М – изгибающий момент и Q – поперечная сила, и чистым, если возникает только М. В поперечном изгибе силовая плоскость проходит через ось симметрии балки, являющейся одной из главных осей инерции сечения.
При изгибе балки одни слои ее растягиваются, другие сжимаются. Между ними находится нейтральный слой, который лишь искривляется, не изменяя при этом своей длины. Линия пересечения нейтрального слоя с плоскостью поперечного сечения совпадает со второй главной осью инерции и называется нейтральной линией (нейтральной осью).
От действия изгибающего момента в поперечных сечениях балки возникают нормальные напряжения, определяемые по формуле
где М – изгибающий момент в рассматриваемом сечении;
|
|
I – момент инерции поперечного сечения балки относительно нейтральной оси;
у – расстояние от нейтральной оси до точки, в которой определяются напряжения.
Как видно из формулы (8.1), нормальные напряжения в сечении балки по ее высоте линейны, достигая максимального значения в наиболее удаленных точках от нейтрального слоя.
где W – момент сопротивления поперечного сечения балки относительно нейтральной оси.
27.Касательные напряжения в поперечном сечении балки. Формула Журавского.
Формула Журавского позволяет определить касательные напряжения при изгибе, возникающие в точках поперечного сечении балки, находящиеся на расстоянии от нейтральной оси x.
ВЫВОД ФОРМУЛЫЖУРАВСКОГО
Вырежем из балки прямоугольного поперечного сечения (рис. 7.10, а) элемент длиной 
и дополнительным продольным сечением рассечем на две части (рис. 7.10, б).
Рассмотрим равновесие верхней части: из-за отличия изгибающих моментов возникают разные сжимающие напряжения. Чтобы эта часть балки находилась в равновесии (
) в ее продольном сечении должна возникнуть касательная сила 
. Уравнение равновесия части балки:
Отсюда
,
где интегрирование ведется только по отсеченной части площади поперечного сечения балки 
(на рис. 7.10, в заштрихована), 
– статический момент инерции отсеченной (заштрихованной) части площади поперечного сечения относительно нейтральной оси x.
Предположим: касательные напряжения (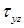
), возникающие в продольном сечении балки, равномерно распределены по ее ширине (
) в месте сечения:
|
|
Получим выражение для касательных напряжений:
, а 
, тогда формула касательных напряжений (
), возникающих в точках поперечного сечения балки, находящихся на расстоянии y от нейтральной оси x:
- формула Журавского
Формула Журавского получена в 1855 г. Д.И. Журавским, поэтому носит его имя.