Полный график критических напряжений представлен на рисунке
раницы применимости решения Эйлера. Формула Ясинского.
Как показали опыты, решение Эйлера подтверждается не во всех случаях. Причина состоит в том, что формула Эйлера была получена в предположении, что при любой нагрузке стержень работает в пределах упругих деформаций по закону Гука. Следовательно, его нельзя применять в тех ситуациях, когда напряжения превосходят предел пропорциональности. В связи с этим найдем границы применимости решения Эйлера:
(30)
Из (30) следует, что напряжение 
возрастает по мере уменьшения гибкости стержня. Заметим, что стержень, имеющий неодинаковые опорные закрепления в главных плоскостях и, следовательно, неодинаковые приведенные длины, теряет устойчивость в той главной плоскости, в которой гибкость стержня имеет наибольшее значение.
Формула Эйлера неприемлема, если напряжения
,
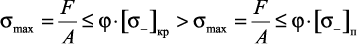где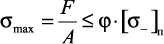 
– предел пропорциональности. Приравнивая (30) к пределу пропорциональности, получим предельное значение гибкости:
Если λ > λпред, то формулу Эйлера можно применять. В противном случае ею пользоваться нельзя. Для стали Ст. 3 – lпред = 100.
В ситуациях, когда напряжения превышают предел пропорциональности, получение теоретического решения осложняется, т.к. зависимость между напряжениями и деформациями становится нелинейной. В связи с этим, в таких случаях пользуются эмпирическими зависимостями. В частности, Ф.С. Ясинский предложил следующую формулу для критических по устойчивости напряжений:
σЕθ = a – bλ, (31)
где a, b – постоянные, зависящие от материала, так для стали Ст. 3 a = 3,1•105 кН/м2, b = 11,4•102 кН/м2.
При гибкостях стержня, находящихся в диапазоне 0 < λ < 40,50, стержень настолько «короток», что его разрушение происходит по схеме сжатия, следовательно, критические напряжения можно приравнять в этом случае к пределу пропорциональности.
Когда формула Эйлера неприменима (за пределом упругости) для определения критической силы можно воспользоваться эмпирической формулой Ясинского П.Ф.
σкр = a – bλ, Fкр = σкрA,
Коэффициент запаса - это отношение некоторого предельного напряжения к максимальному напряжению, возникаемому в конструкции.
Максимальное напряжение в конструкции не должно превышать допускаемого напряжения для данного материала определенного с учетом коэффициента запаса для заданных условий работы.
Коэффициент запаса - число большее единицы.
35.Условие устойчивости. Три типа задач.
Условием устойчивости сжатого стержня является неравенство:
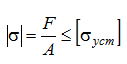
Здесь допускаемое напряжение по устойчивости [σ уст ] — не постоянная величина, как это было в условиях прочности, а зависящая от следующих факторов:
1) от длины стержня, от размеров и даже от формы поперечных сечений,
2) от способа закрепления концов стержня,
3) от материала стержня.
На основании условия устойчивости решаются три вида задач:
- Проверка устойчивости.
- Подбор сечения.
- Определение допускаемой нагрузки (или безопасной нагрузки, или грузоподъемности стержня: [ F ]=φ[σ] А.
Наиболее сложным оказывается решение задачи о подборе сечения, поскольку необходимая величина площади сечения входит и в левую, и в правую часть условия устойчивости:
Только в правой части этого неравенства площадь сечения находится в неявном виде: она входит в формулу радиуса инерции 
, который в свою очередь включен в формулу гибкости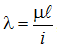 
, от которой зависит значение коэффициента продольного изгиба φ. Поэтому здесь приходится использовать метод проб и ошибок, облеченный в форму способа последовательных приближений:
1 попытка: задаемся φ1 из средней зоны таблицы, находим 
, определяем размеры сечения, вычисляем , затем гибкость 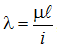, по таблице определяем 
и сравниваем со значением φ1. Если 
, то:
2 попытка: принимаем 
, находим 
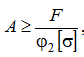, определяем размеры сечения, вычисляем , затем гибкость 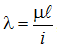, по таблице определяем 
, и если 
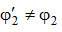, то:
3 попытка: принимаем 
, находим 
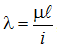, определяем размеры сечения, вычисляем , затем гибкость , по таблице определяем 
, и т.д.
Процесс приближений продолжается до тех пор, пока разница не окажется менее 5%.