| aω,1-й ряд | m мм | q | Z2 /Z1= u | aω, мм, 1-й ряд | m, мм | q | Z2 /Z1= u |
| 32:4 32:2 32:1 | 1,6 | 40:4 40:2 40:1 | |||||
| 2,5 | 32:4 32:2 32:1 | 40:4 40:2 40:1 | |||||
| 3,15 | 32:4 32:2 32:1 | – | – | – | |||
| 32:4 32:2 32:1 | – | – | – | ||||
| 32:4 32:2 32:1 | 40:4 40:2 40:1 | ||||||
| 40:4 40:2 40:1 | 12,5 | 50:4 50:2 50:1 | |||||
| 140* | 40:4 40:2 40:1 | 140* | 46:4 46:2 46:1 | ||||
| 32:4 32:2 32:1 | – | – | – | ||||
| 32:4 32:2 32:1 | 40:4 40:2 40:1 | ||||||
| 12,5 | 32:4 32:2 32:1 | 40:4 40:2 40:1 | |||||
| 12,5 | 50:4 50:2 50:1 | – | – | – | – | ||
| 280* | 40:4 40:2 40:1 | 280* | 46:4 46:2 46:1 | ||||
| 32:4 32:2 32:1 | 40:4 40:2 40:1 | ||||||
| 40:4 40:2 40:1 | 12,5 | 50:4 50:2 50:1 |
* 2-й ряд.
В таблице 9.2 даны сочетания модулей m и коэффициентов q диаметра червяка.
Таблица 9.2.
Сочетания m и q
| m, мм | q | m, мм | q | m, мм | q | m, мм | q |
| 1,6 | 3,15 | 6,3 | 12,5 | ||||
| 1,6 | 12,5 | 3,15 | 6,3 | 12,5 | |||
| 1,6 | 3,15 | 12,5 | 6,3 | 12,5 | 12,5 | 12,5 | |
| 1,6 | 3,15 | 6,3 | 12,5 | ||||
| 3,15 | 6,3 | 12,5 | |||||
| 6,3 | |||||||
| 12,5 | |||||||
| 12,5 | 12,5 | ||||||
| 12,5 | |||||||
| 2,5 | |||||||
| 2,5 | |||||||
| 2,5 | 12,5 | 12,5 | |||||
| 2,5 | 12,5 | ||||||
| 2,5 | 12,5 | – | – | ||||
| – | – | – | – | – | |||
| – | – | – | – | – | – |
2. Расчет на контактную выносливость ведут как проектный, определяя требуемое межосевое расстояние: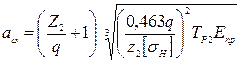 
, (9.13)
|
|
где [σН] – допускаемое контактное напряжение; Тр2 = Т2К – расчетный момент на валу червячного колеса; К – коэффициент нагрузки; Eпр = 2Е1Е2 / (Е1 + Е2 )– приведенный модуль упругости (Е1 – модуль упругости материала червяка, Е2 – модуль упругости венца червячного колеса).
Формула справедлива при любых взаимно согласованных единицах измерения входящих в нее величин.
Формула (9.13) и формулы (9.15), (9.18), (9.20 и (9.23) соответствуют наиболее распространённой форме венца червячного колеса, при которой условный угол обхвата 2 
= 100° (см. рис. 9.2). При ином значении числовые коэффициенты в указанных формулах следует умножить на коэффициент
. (9.14)
В начале расчета предварительно принимают q = 8 или 10, а для слабонагруженных передач ( Т2 < 300 Нм) q = 12,5 или 16. Значения [σН] выбирают по табл. 6.4. Приведенный модуль упругости Епр определяют по известным значениям модулей упругости материалов червяка и венца червячного колеса.
Для стали Е1 =2,1x105 МПа; для чугуна Е2= (0,885…1,13) x105 МПа; для бронзы Е2 = (0,885–1,13) 105 МПа (большие значения – для твердых безоловянныхбронз).
Средние значения модуля упругости чугуна и бронзы примерно одинаковы, поэтому для сочетания материалов сталь – чугун формулу (9.13) можно упростить, введя среднее значение Епр = 1,32x105 МПа.
. (9.15)
где Т2 – в Нмм; аω – в мм; [σН] – в МПа.
После определения аω следует найти модуль зацепления из соотношения:
|
|
m = 2 аω / (q + z2). (9.16)
Пусть, например, при z1 = 2; z2 = 32 и q =10 было получено по ф-ле (9.15) межосевое расстояние аω = 78. Вычисляем модуль m = 2∙78 /(10+32) = 3,73 мм.
По табл. 9.1 принимаем m = 4 мм и убеждаемся, что при этом стандартном значении модуля имеется q = 10. Тогда межосевое расстояние
аω = 0,5(q + z2) m = 0,5(10+32)∙4 = 84 мм.
Желательно, чтобы окончательно принятое значение межосевого расстояния выражалось целым числом миллиметров (предпочтительно из стандартного ряда (табл. 9.1). Для этого в отдельных случаях (если допустимо некоторое отступление от заданной величины передаточного числа) надо увеличить или уменьшить z2 на один-два зуба. Например, для получения передаточного числа 15,5 было принято z1= 2; z2 = 31; после округления параметров получено
m = 5 мм и q = 10. Тогда аω = (q +z2)m = 0,5(10+31)x 5 =102,5мм. Целесообразно принять z2 =32; тогда аω = (q +z2)m= 0,5(10+32)x5 =105мм.
При этом передаточное число 32/2 =16.
Отклонение от заданного (16-15,5)/15,5 ∙100% =3,2% при допускаемом 4%.
Если по заданию курсового проекта предусмотрено массовое изготовление проектируемого редуктора, то следует согласовать с ГОСТ не только величины m и q, но и величины аω, z1иz2.Так согласовывая наш пример с табл. 9.1, будем иметь редуктор с параметрами: аω =100мм.,m = 5мм., q = 8,
z2 / z1 = 32:2.
После окончательного установления параметров зацепления следует уточнить коэффициент нагрузки, допускаемое напряжение и проверить расчётные контактные напряжения.
При любом сочетании материалов червяка и колеса
; (9.17)
при стальном червяке и червячном колесе, изготовленном из чугуна или имеющем бронзовый венец:
, (9.18)
или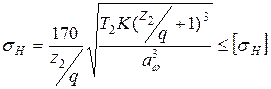 
. (9.19)
|
|
Результат проверочного расчёта следует признать удовлетворительным, если
превышает 
не более чем на 5%.
3.Расчёт зубьев червячного колеса на выносливость по напряжениямизгиба (зубья колеса обладают меньшей прочностью чем витки червяка) выпол-
няют по формуле:
, (9.20)
где σF – расчётное напряжение изгиба; Т2К – расчётный момент на валу червячного колеса; Ft2 – окружная сила на червячном колесе; К – коэффициент нагрузки (см. в гл. 9.4).
Ft2 – определяют по известному моменту на валу червячного колеса:
Ft2 = 2T2 / d2.
ΥF – коэффициент формы зуба, принимаемый по табл. 9.3 в зависимости от эквивалентного числа зубьев червячного колеса: zv = z2 / Cos3 γ;
– коэффициент, учитывающий ослабление зубьев в результате износа.
для редукторов; 
1,15 для открытых передач.
– допускаемое напряжение изгиба приведено в табл. 6.4.
Таблица 9.3.
Коэффициент формы зуба ΥF для червячных передач
| zv | ||||||||||
| ΥF | 2,43 | 2,41 | 2,32 | 2,27 | 2,22 | 2,19 | 2,12 | 2,09 | 2,08 | 2,04 |
При расчёте по формулам (9.19) и (9.20) напряжения следует принимать в МПа; силы в Н; линейные размеры в мм.
4. Расчёт коэффициента нагрузки для червячных передач производится по формуле: K = K β K v, где К β – коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий; Кv - коэффициент, учитывающий динамическую нагрузку, возникающую в зацеплении.
Коэффициент Кβ зависит от характера изменения нагрузки и от деформации червяка
, (9.21)
где Ω – коэффициент деформации червяка, определяемый по табл. 9.4:
Таблица 9.4.
Значения коэффициента деформации червяка Ω
| z1 | Значение q | |||||
| 12.5 | ||||||
x – вспомогательный коэффициент, зависящий от характера изменения нагрузки:
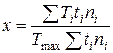, (9.22)
где Ti; ti;,ni, – соответственно вращающий момент, продолжительность и частота вращения при режиме i; Tmax – максимальный длительно действующий момент. В расчётах, когда не требуется высокая точность, можно принимать: при постоянной нагрузке x=1; при незначительных колебаниях нагрузки x = 0,6; при значительных колебаниях нагрузки x = 0,3.
При постоянной нагрузке коэффициент Кβ = 1.
Коэффициент K v зависит от точности изготовления передачи и от скорости скольжения vs (табл. 9.5). По этой таблице можно назначать степень точности передачи.
Таблица 9.5.
Коэффициент динамичности нагрузки K v
| Степень точности | Скорость скольжения vs, м/с. | |||
| До 1,5 | Св. 1,5 до3 | Св. 3 до 7,5 | 7,5 – 12 | |
| – | – | 1,1 | ||
| 1,0 | 1,0 | 1,1 | 1,2 | |
| 1,15 | 1,25 | 1,4 | – | |
| 1,25 | – | – | – |
Примечание. По Гост 3675-81 установлено 12 степеней точности для червячных передач. Для силовых установок предназначены от 5-й до 9-й в порядке убывания точности; для редукторов общего применения применяют в основном 7-ю и 8-ю степени точности.
5. Расчёт жёсткости червячного зацепления
Под действием сил в червячном зацеплении червяк и вал червячного колеса прогибаются и правильность зацепления нарушается, что приводит к ускоренному износу. В основном это уже учтено при выборе коэффициента диаметра червяка, но всё равно прогиб вала червяка или вала червячного колеса y не должен быть более допустимой величины в зависимости от модуля зацепления. 
. Величину прогиба вычисляют по известным зависимостям курса «Сопротивление материалов» и курса «Детали машин».
6. Расчёты на контактную выносливость при изгибе
Зубья червячного колеса являются расчётным элементом зацепления, так как они имеют меньшую поверхностную и общую прочность, чем витки червяка.
Зубья червячных колес рассчитывают так же, как и зубья зубчатых колес – на контактную выносливость и на выносливость при изгибе; расчет на контактную прочность должен обеспечить не только отсутствие выкрашивания рабочих поверхностей зубьев, но и отсутствие 
заедания, приводящего к задирам рабочих поверхностей зубьев.
На рис. 9.3 представлена расчётная схема вала червячного колеса. Показаны силы в зацеплении: Ft2 – окружная, Fr2 – радиальная, Fa2 – осевая; реакции опор в плоскостях действия сил
R y3, R y4, R z3, R z 4; эпюра изгибающих моментов My от действия силы Ft2, эпюра изгибающих моментов Mz от действия сил Fa2 и Fr2 и эпюра крутящего момента Т2. Расстояние между опорами (центрами подшипников) – l2 и червячное колесо расположено центрально относительно опор.
Для данного случая стрела прогиба вала
, где – Е модуль упругости материала вала, J – осевой момент инерции сечения вала под червячным колесом.
, где d – диаметр вала.
Рис. 9.3. Расчётная схема
Формулы для определения величины прогиба и угла поворота вала приведены в источнике [4]для различных схем нагружения.
6.Тепловой расчёт червячных редукторов
Одним из основных недостатков червячной передачи является повышенное трение в зацеплении и, как следствие, выделение избыточного тепла, которое необходимо отводить, иначе смазка под воздействием тепла разлагается и зацепление выходит из строя. В стандартных редукторах принято, что разница температуры внутри картера редуктора и температуры внешней среды не должна превышать 60…700 С. При такой разнице температур обычные рекомендуемые смазки устойчиво работают.
, (9.23)
где t m – температура масла в картере редуктора при длительной работе;t b – температура окружающей среды (температура в цехе); Р1 – подводимая мощность, Вт;η – КПД редуктора;kt – коэффициент теплопередачи, Вт /(м2 ∙ 0С) равен 17 без принудительного обдува.
Если по расчётам получается превышение требуемой разницы температур, то необходимо увеличить площадь редуктора, сделав корпус ребристым. Нужно учесть также условия монтажа редуктора. Если он установлен на сплошной раме, то площадь его основания не входит в площадь теплоотдачи. Можно увеличить коэффициент теплопередачи на 25%, если установить на входной вал редуктора крыльчатку вентилятора.
Чертежи различных червячных редукторов приведены в источниках [2], [6].
Студентам рекомендуется внимательно изучить по литературе различные конструкции червячных редукторов, прежде чем приступить к разработке собственной конструкции.
Рис. 9.4. Чертёж одноступенчатого червячного редуктора