Элементарные функции алгебры логики

В число ФАЛ, подсчитываемых с помощью теоремы 1.1 входят как функции существенно зависящие от всех n аргументов, так и функции, для которых часть из этих аргументов фиктивна. Например, для n=1 имеем 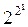=4 различных функций, приведенных в следующей таблице:

1

Из таблицы видно, что только и существенно зависят от , а для и этот единственный аргумент является фиктивным. Функция (x), повто-ряющая значение логической переменной - тождественная функция ( (x) º x), а функция (x) - принимающая значения, обратные значениям x - логическое отрицание, или функция отрицания, или инверсии, или функция НЕ ( (x) = ).

Теорема 1.2. Число ФАЛ, существенно зависящих от n аргументов, определяется следующим рекуррентным соотношением:

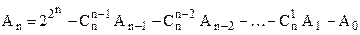, (1.3)

где - биномиальные коэффициенты. 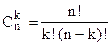, - число ФАЛ, существенно зависящих от i аргументов.

Правая часть соотношения есть разность между числом всех ФАЛ и суммой всех ФАЛ, существенно зависящих от любого числа аргументов, меньших чем n.

Вместо рекуррентного соотношения 1.3 можно найти прямое выражение для значений . Как показал Крылов Г. А.

. (1.4)

Пример Найти число ФАЛ, существенно зависящих от 3-х переменных.

Имеем: =2.

Действительно

.

.

.

Итак, в случае n=0 имеем в силу теоремы 1.1 две функции, совпадающие с константами 0 и 1.

= 0; = 1 (1.5)

При n =1 имеем 2 функции, существенно зависящих от x

= x; = (не ' x '). (1.6)

Рассмотрим логические функции от 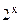переменных:

Функции					Примечание.
	0 0	0 1	1 0	1 1
					¦ º 0
					¦ = = Ù = & конъюнкция.
					¦ = (запрет )
					¦ = (тождественность )
					¦ = (запрет )
					¦ = (тождественность )
					¦ = ( ) (сложение по модулю 2)
					¦= Ú = + (дизъюнкция)
					(Функция Пирса)
					~ )(Равнозначность)
					¦ = (Отрицание )
					¦ = ( ® ) (Импликация)
					¦ = (Отрицание )
					¦ = ( ® ) (Импликация)
					¦ = ( / ) (Функция Шеффера)
					¦ º 1

В силу теоремы 1.2 имеем 10 различных функций, существенно зависящих от аргументов и . Из них рассмотрим семь, которые играют большую роль в построении теории ФАЛ и ее приложениях. (Помимо рассмотренных 1.5 и 1.6).

а). Функция ¦ = = Ù = & конъюнкция (логическое умножение, или функция И) истинна тогда и только тогда, когда и и истинны.

		¦

б). Функция ¦ = Ú - дизъюнкция (логическое сложение, или функция ИЛИ) истинна тогда, и только тогда, когда истинныили , или , или обе переменные.

		¦

в). Функция ¦ = ( ) Функция сложения по модулю 2 ( или функция разноименности, или функция исключающее ИЛИ) истиннатогда,когдаистиннаили , или , но не обе вместе.

		¦

г).Функция - ~ ) функция равнозначности, которая истинна тогда и только тогда, когда обе переменные илиистинны, или ложны.

		¦

д.) Функция ¦ = ( ® ) (импликация в ), которая ложна тогдаи только тогда, когда истинна, а ложна

		¦= ®	¦= ®

.

е.) Функция - функция Пирса (Вебба), которая истиннатогда и только тогда, когда и ложны.

		¦

ж.) Функция ¦ = ( / ) (Функция Шеффера), которая ложнатолько тогда, когда и истинны.

		¦

Для наглядности рассмотренные функции сведены в общую таблицу:

		&	Ú			®	®		/

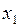Рассмотренные 11 функций алгебры логики называются элементарными и позволяют строить новые ФАЛ двумя основными путями:

1. Путем перенумерации аргументов (для некоторых функций)

2. Путем подстановки в функцию новых функций вместо аргументов.

Функцию, полученную из функций путем применения (возможно многократного) этих двух правил, называют суперпозицией функций .