1. Выбрать в таблице задания функции все наборы аргументов, на которых функция обращается в нуль.
2. Выписать дизъюнкции, соответствующие этим наборам аргументов. При этом, если аргумент 
входит в данный набор как 0, он выписывается без изменения в дизъюнкцию, соответствующему данному набору. Если же входит в данный набор как 1, то в соответствующую дизъюнкцию выписывается его отрицание.
3. Все полученные дизъюнкции соединяются между собой знаками конъюнкций.
Пример (см. табл. 1.5.1.):
= 
&
& 
&
& 
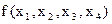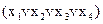
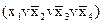
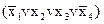
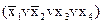Если в выражении 1.32 использовать вместо конъюнкции эквивалентность, то мы получим представление в форме 1.27.
Представление ФАЛ в импликативной форме
Теорема 1.6. Любая ФАЛ, кроме тождественной единицы, может быть представлена в следующей форме:
ѓ 
=. 
(1.33)
Доказательство. Для любого набора значений аргументов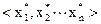 
, для которого f =0, найдется в конъюнкции импликация 
= 
,
обращающаяся в нуль на этом наборе и принимающая значения 1 на всех остальных наборах. Для этого достаточно вхождения всех аргументов , кроме 
в с отрицанием, если 
=1 и без отрицания в противном случае. Для условия вхождения противоположны. Конъюнкцию в 1.33 можно заменить при желании импликацией и отрицанием т.к. 
= 
*
Пример. Записать ФАЛ табл. 1.5.1 в импликативной форме.
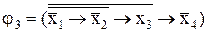
и тогда ѓ 
= 
&
& 
&
& 
&
& 
.
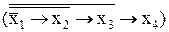
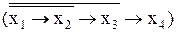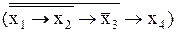
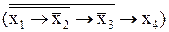Применив * получим:
f = 
Импликативная форма записи является аналогом СНКФ.
Теорема 1.7. Любая ФАЛ, кроме тождественного нуля, может быть представлена в форме:
f = 
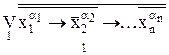(1.34)
Для доказательства 1.34 достаточно заметить, что функции 
устроены так, что каждая такая функция обращается в единицу на наборе, соответствующем набору < 
> и равна 0 на остальных. Дизъюнкция 1.34 может быть заменена через импликацию и отрицание 
|
|
Пример. Записать ФАЛ табл. 1.5.1. в импликативной форме (ИДФ)
. 
. 
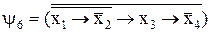
и тогда f = 
V 
V
V 
V 
V 
V
V 
V 
и применив ** получим:
f = 
.
Представление ФАЛ в виде полинома Жегалкина
Согласно свойствам функции сложения по модулю два, которая имеет еще множество различных названий (неравнозначности, исключающее ИЛИ, нетождественности, разноименности и т.п.) для двух переменных мы имеем следующие равносильности:
(свойство коммутативности);
(свойство ассоциативности);
(свойство дистрибутивности).
На основе свойства ассоциативности рассматривается многоместная операция сложения по модулю два 
, которая принимает значения логической единицы тогда и только тогда, когда в ней содержится четное количество единиц. Именно на этой операции основан контроль передачи двоичных слов по линиям связи в цифровых устройствах.
Теорема Жегалкина. Любая ФАЛ может быть представлена в виде:
где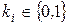 
.
Доказательство. Запишем ФАЛ в совершенной полиноминальной форме:
. (1.35)
Поскольку 
то 
Подставив в (1.35) вместо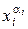 
выражение 
, получаем:
.
Раскрыв скобки (свойство дистрибутивности) и на основании правила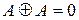 
, приводим функцию к виду
,
где коэффициенты 
равны 0 или 1. Коэффициент, соответствующий пустому множеству индексов 
представляет собой свободный член полинома. Указанное представление носит название полинома Жегалкина.