(Карты Карно)
Один из способов графического представления ФАЛ от небольшого числа переменных - использование карт Карно. Их разновидность - карты Вейча, которые строят как развертки кубов на плоскости. При этом вершины куба представляются клетками карты, координаты которых совпадают с координатами соответствующих вершин куба. Карта Карно заполняется также, как таблица истинности: В каждой клетке, соответствующей набору, проставляется значение функции. Переменные размещаются на карте так, что при переходе из одной клетки в любую соседнюю, должна изменяться только одна переменная. Нижний ряд карты следует рассматривать как примыкающий к верхнему ряду, а левый ряд - к правому.
Карты Карно для:
2-х переменных 3-х переменных 4-переменных.

Если требуется получить карту Карно для какой-нибудь функции, то сначала записывают эту функцию в НДФ. Каждый член, который появляется в этой форме, задается на карте Карно с помощью 1 в соответствующей клетке. Затем группируют единицы в соответствующих полях, очерчивая их замкнутыми линиями. При изучении карты с очерченными полями оказывается, что если две соседние клетки содержат 1, то из них всегда можно удалить одну переменную, а именно ту переменную, для которой ее инверсия располагается в следующей соседней клетке. Рассмотрим примеры для функций 2-х, 3-х и 4-х переменных.
1. 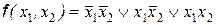 .
.
Имеем следующую карту Карно:
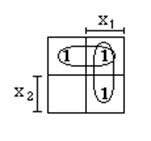
И тогда в минимальной форме функцию можно представить как:
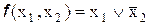 .
.
2. 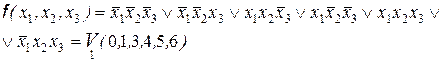
Для этой функции карта Карно будет иметь вид:
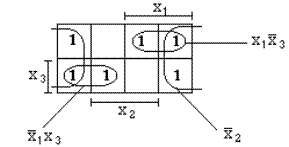
После минимизации получаем:
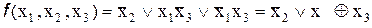 .
.
3. 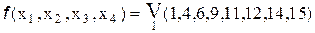 .
.
Получаем:
4. 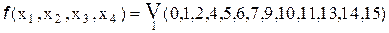
Вполне очевидно, что логическую функцию в последнем примере можно представить в минимальной форме и другими вариантами, объединяя ”1” по иному.
Карты Карно для числа переменных n>4 составляются из идентичных (в смысле обозначения сторон первичными термами) карт для четырех переменных.
Две карты Карно для четырех переменных будем называть соседними, если они имеют общую грань. Клетки, расположенные в одинаковых местах соседних карт для четырех переменных, являются соседними, т.к. им соответствуют соседние минтермы.
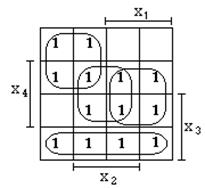
Например, для n=5
Соседними клетками здесь являются: 0 и 16, 1 и 17, 7 и 23, 14 и 30, 8 и 24 и т.п.
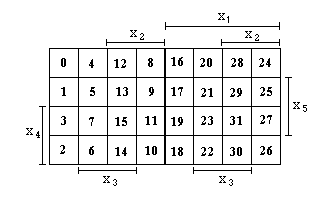
При n=6 имеем:
Здесь соседними являются клетки: 0 и 32, 0 и 16, 5 и 37, 5 и 21, 14 и 30, 14 и 46 и т.п. Но 0 и 48, 18 и 34, 15 и 63 и т.п. не являются соседними.
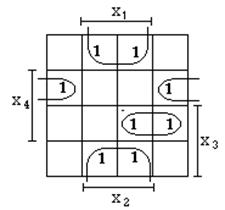
Пример. Минимизировать ФАЛ:
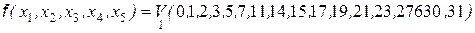
В соответствии с вышеизложенным получаем карту Карно, вид которой представлен на рис. 2.4.
И в результате минимизации получим:
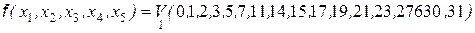 =
=
=  .
.
Вполне очевидно, что располагая поля переменных иным образом, но соблюдая правила составления карт Карно, должна получиться такая же минимальная функция. (По числу термов и их длине).
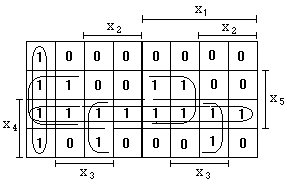
Рис. 2.4.
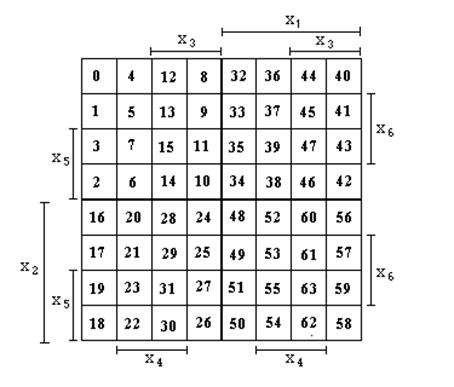
Пример. Минимизировать ФАЛ:
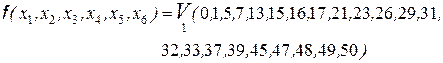
Заполняя карту Карно для n=6 получаем:

Результат минимизации будет представлен в данном случае как:
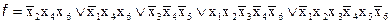 .
.
Карты Карно используют и для получения минимальных КНФ. Это вытекает из принципа двойственности и законов двойственности. Покажем это на примере.
Пусть имеем ФАЛ 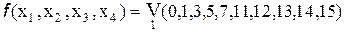 .
.
Минимизируя с помощью карты Карно (рис.2.5) получаем:
 .
.
Тогда имеет место в данном случае следующее соотношение:
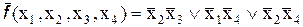 ,
,
откуда на основании двойственности получаем:
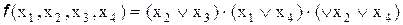 .
.
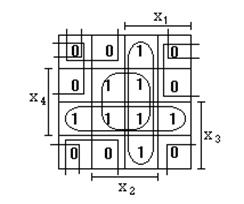
Рис. 2.5.