СНДФ.
Рассмотрим конъюнкцию  (1.29)
(1.29)
Набор < 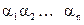 > двоичный и существует
> двоичный и существует  таких различных наборов. Т.о., число различных конъюнкций вида 1.29 также равно
таких различных наборов. Т.о., число различных конъюнкций вида 1.29 также равно  .
.
Сопоставим каждой конъюнкции (1.29) номер, определяемый номером набора < 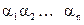 >. Тогда запись:
>. Тогда запись:
 (
( )
)
означает дизъюнкцию всех конъюнкций с номерами из множества  .
.
Аналогично, запись  (
( ) означает конъюнкцию всех дизъюнкций с номерами из множества
) означает конъюнкцию всех дизъюнкций с номерами из множества  .
.
Покажем, что 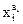 =1 тогда и только тогда, когда выполняется равенство
=1 тогда и только тогда, когда выполняется равенство  . Это вытекает из рассмотрения следующих четырех возможных случаев.
. Это вытекает из рассмотрения следующих четырех возможных случаев.
1.  3.
3. 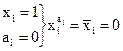
2. 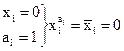 4.
4. 
Таким образом, конъюнкция  не обращается в нуль только в том случае, если одновременно выполняются следующие i равенств.
не обращается в нуль только в том случае, если одновременно выполняются следующие i равенств.
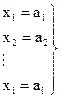 (1.30)
(1.30)
Из 1.30 вытекает, что  (
( )=
)=  при условии, что
при условии, что
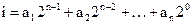
Тогда на основании теоремы 1.3 можно утверждать, что любая ФАЛ, кроме нуля, может быть представлена в виде:
¦( )=
)= 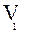 (
( ) (1.31)
) (1.31)
При этом дизъюнкция берется только по тем номерам наборов аргументов, на которых функция, заданная таблицей, обращается в единицу. Представление функции в виде 1.31 называется дизъюнктивной совершенной нормальной формой, (ДСНФ) или совершенной нормальной дизъюнктивной формой (СНДФ).
Алгоритм перехода из таблично заданной ФАЛ к СНДФ.
1. Выбрать в таблице задания функции все наборы аргументов, на которых функция обращается в единицу.
2. Выписать конъюнкции, соответствующие этим наборам аргументов. При этом, если аргумент  входит в данный набор как 1, он выписывается без изменения в конъюнкцию, соответствующую данному набору. Если же
входит в данный набор как 1, он выписывается без изменения в конъюнкцию, соответствующую данному набору. Если же  =0, то в соответствующую конъюнкцию вписывается его отрицание.
=0, то в соответствующую конъюнкцию вписывается его отрицание.
3. Все полученные конъюнкции соединяются между собой знаками дизъюнкции.
Пример. Пусть имеем таблично заданную ФАЛ:
Табл. 1.5.1.

| 
| 
| 
| ¦( , ,  , ,  , ,  ) )
| ||

| ||||||
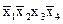
| ||||||
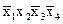
| ||||||

| ||||||

| ||||||

| ||||||
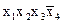
| ||||||
и тогда имеем:
¦( ,
,  ,
,  ,
,  )=
)=  v
v 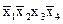 v
v 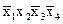 v
v  v
v
v  v
v  v
v 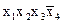
Если вместо соотношения 1.23 воспользоваться соотношением 1.24, то получим совершенно нормальную полиноминальную форму СНПФ. СНПФ получается из СНДФ заменой знака V на Å. Так, в рассмотренном примере функция в СНПФ будет иметь вид:
¦( ,
,  ,
,  ,
,  )=
)=  Å
Å 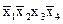 Å
Å 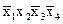 Å
Å  Å
Å  Å
Å
Å  Å
Å 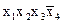
Совершенная нормальная конъюктивная форма(СНКФ)
Теорема 1.5. Любая ФАЛ, кроме единицы, может быть представлена в виде:
 (1.32.)
(1.32.)
Символ  означает, что & берется только по тем наборам
означает, что & берется только по тем наборам 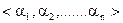 ,
,
для которых выполняется равенство:  =0.
=0.
Доказательство:
Имеем:  или
или
 .
.
Равенство не нарушается, если от обеих частей взять отрицание:
. 
Применяя закон де - Моргана получаем:
 На тех наборах, для которых
На тех наборах, для которых  , соответствующая дизъюнкция
, соответствующая дизъюнкция
 .
.
И такие наборы на значение конъюнкции не влияют  и ими можно пренебречь, и тогда:
и ими можно пренебречь, и тогда:
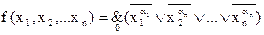
Теорема доказана для всех  .
.
Представление функции в виде 1.32 называется СНКФ – совершенной нормальной конъюктивной формой.
Из сравнения (1.26) и (1.32) вытекает, что  ,
,
при условии, что  .
.