Итак мы установили, что для логической переменной  и
и 
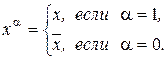
Вполне очевидно, что  тогда и только тогда, когда
тогда и только тогда, когда  . Следовательно, конъюнкция
. Следовательно, конъюнкция  равна 1 на единственном наборе значений аргументов, когда
равна 1 на единственном наборе значений аргументов, когда  , т.е.
, т.е.  .
.
Теорема о разложении ФАЛ. Любая ФАЛ  для любого
для любого  (
( может быть представлена в виде:
может быть представлена в виде:
 ,
,
где дизъюнкция берется по всевозможным наборам  значений аргументов
значений аргументов  .
.
Доказательство. Для доказательства необходимо и достаточно показать, что для любого набора аргументов ( ) левая и правая часть формулы принимают одинаковые значения.
) левая и правая часть формулы принимают одинаковые значения.
Рассмотрим правую часть. Поскольку  0 когда
0 когда

 и
и  1, то
1, то

 , т.е совпадает со значением левой части. Теорема доказана.
, т.е совпадает со значением левой части. Теорема доказана.
Например, если функцию 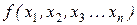 представить в виде разложения, например, по переменной
представить в виде разложения, например, по переменной  , то она будет выглядеть следующим образом:
, то она будет выглядеть следующим образом:
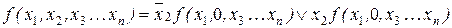 .
.
Пример. Функцию  разложить по переменным а и b.
разложить по переменным а и b.
Т.к. функцию требуется разложить по двум переменным, следовательно, она будет представлена четырьмя слагаемыми:

 .
.
Нетрудно увидеть, что метод разложения ФАЛ по переменным является простым и эффективным средством упрощения ФАЛ для представления их, например, в ДНФ.
Основные классы ФАЛ
Для решения ряда принципиальных вопросов, связанных с теорией функций алгебры логики и с практическим применением результатов этой теории для анализа и синтеза схем, полезно рассмотреть основные классы функций алгебры логики.
Пусть имеются логические функции  и
и  . Будем считать, что функции
. Будем считать, что функции  зависят от одних и тех же аргументов
зависят от одних и тех же аргументов 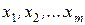 (этого можно достигнуть, добавив, при необходимости, к аргументам некоторых из функций фиктивные аргументы). Функцию
(этого можно достигнуть, добавив, при необходимости, к аргументам некоторых из функций фиктивные аргументы). Функцию

называют суперпозицией функций q и  . Рассмотрим некоторый класс A логических функций.
. Рассмотрим некоторый класс A логических функций.
Определение: Класс А называется замкнутым, если для всяких функций 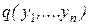 и
и  из А их суперпозиция
из А их суперпозиция  содержится в А.
содержится в А.
Приведем некоторые важные примеры замкнутых классов.
Класс функций, сохраняющих константу нуль, т.е. таких функций, для которых имеет место f (0,0,0,...,0)=0. Обозначим этот класс 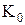 . Очевидно, что при фиксированном n число функций этого класса составляет половину всех ФАЛ, т.е.
. Очевидно, что при фиксированном n число функций этого класса составляет половину всех ФАЛ, т.е.  .
.
Аналогично, класс функций, сохраняющих константу единица определен как класс функций, для которых f (1,1,...,1)=1. Этот класс, состоящий также из  функций, обозначен символом
функций, обозначен символом  .
.
Определение: Функция  называется двойственной к функции
называется двойственной к функции  , если имеет место равенство:
, если имеет место равенство:
 =
= 
Принципы и законы двойственности.
Принципы двойственности можно записать следующим образом: Если имеет место тождество  , где
, где  , то справедливо также тождество
, то справедливо также тождество 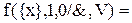
 , т.е. если в каком-либо тождестве произвести взаимную замену символов 0 и 1 (если они имеются) и операций V и &, то будет получено также тождество. Два тождества, связанные между собой таким образом, являются двойственными. Истинность самого принципа двойственности не доказывается, т.к. данный принцип является внутренним свойством алгебры логики (заключен в ее аксиомах). Законы двойственности (теоремы де-Моргана) устанавливают способ отыскания инверсных функций, представляющих собой V и & 2-х переменных. Клод Шеннон предложил обобщение этих теорем, позволяющее отыскивать инверсию любой функции
, т.е. если в каком-либо тождестве произвести взаимную замену символов 0 и 1 (если они имеются) и операций V и &, то будет получено также тождество. Два тождества, связанные между собой таким образом, являются двойственными. Истинность самого принципа двойственности не доказывается, т.к. данный принцип является внутренним свойством алгебры логики (заключен в ее аксиомах). Законы двойственности (теоремы де-Моргана) устанавливают способ отыскания инверсных функций, представляющих собой V и & 2-х переменных. Клод Шеннон предложил обобщение этих теорем, позволяющее отыскивать инверсию любой функции  f {x}, где {x}=
f {x}, где {x}= 
 .
.
Закон двойственности, установленный Шенноном имеет вид:  , где {x}=
, где {x}=  , {
, {  }=
}=  .
.
Т.е. инверсию любой функции f({x}) можно получить взаимной заменой переменных  и их инверсий
и их инверсий  (i=1,2,.....n) и операций V и &.
(i=1,2,.....n) и операций V и &.
Пример:
 , тогда
, тогда  .
.
На основании закона двойственности легко показать, что
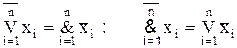 .
.
Определение Функция  называется самодвойственной, если она совпадает с двойственной себе функцией, т.е. имеет место равенство
называется самодвойственной, если она совпадает с двойственной себе функцией, т.е. имеет место равенство
 =
=  .
.
Класс самодвойственных функций обозначим символом S. Число членов этого класса равно  , т.к. самодвойственная функция от n аргументов полностью определяется на половине наборов значений аргументов.
, т.к. самодвойственная функция от n аргументов полностью определяется на половине наборов значений аргументов.
Определение. Функция  называется линейной, если она представима в следующем виде:
называется линейной, если она представима в следующем виде:
 ,
,
где 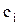 может принимать значения 0 или 1. Класс линейных функций обозначим буквой L. Число членов этого класса равно
может принимать значения 0 или 1. Класс линейных функций обозначим буквой L. Число членов этого класса равно 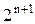 .
.
Набор значений аргументов  не меньше набора значений аргументов
не меньше набора значений аргументов  , если между всеми компонентами наборов
, если между всеми компонентами наборов 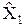 и
и  установлено соотношение
установлено соотношение  . Например, набор <1,1,0, 1,0> не меньше набора <1,0,0,1,0>, а наборы <1,1,0,1,0> и <1,0,1,1,0> несравнимы.
. Например, набор <1,1,0, 1,0> не меньше набора <1,0,0,1,0>, а наборы <1,1,0,1,0> и <1,0,1,1,0> несравнимы.
Определение. Функция  называется монотонной, если для двух наборов
называется монотонной, если для двух наборов 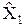 и
и  таких, что
таких, что 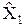
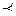
 имеет место равенство
имеет место равенство
 .
.
Класс монотонных функций обозначим буквой M. Число функций класса M оценивается асимптотически формулой
 ,
,
где  - число монотонных функций алгебры логики, A- константа. Нижняя оценка получена Э.Н. Гильбертом, верхняя- В.К. Коробовым.
- число монотонных функций алгебры логики, A- константа. Нижняя оценка получена Э.Н. Гильбертом, верхняя- В.К. Коробовым.
Определение. Функция  называется симметричной, если она не изменяется при произвольной перенумерации аргументов.
называется симметричной, если она не изменяется при произвольной перенумерации аргументов.
 =
=  ,
,
где  - любая перестановка аргументов
- любая перестановка аргументов  .
.
Полные системы функций
Определение. Система функций алгебры логики 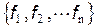 называется полной в классе R, если любая функция
называется полной в классе R, если любая функция  , принадлежащая R, может быть представлена суперпозицией функций
, принадлежащая R, может быть представлена суперпозицией функций  .
.
Определение. Система функций 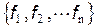 , являющаяся полной в классе R, называется базисом. Или: Базисом называется полная система ФАЛ, с помощью которой любая ФАЛ может быть представлена суперпозицией исходных функций.
, являющаяся полной в классе R, называется базисом. Или: Базисом называется полная система ФАЛ, с помощью которой любая ФАЛ может быть представлена суперпозицией исходных функций.
Определение. Минимальным базисом называется такой базис, для которого удаление хотя бы одной из функций  , образующих этот базис, превращает систему функций
, образующих этот базис, превращает систему функций 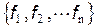 в неполную.
в неполную.
В силу теоремы 1.1, общее число различных функций, зависящих от n аргументов, равно  . Поэтому существует тривиальная полная система
. Поэтому существует тривиальная полная система  , состоящая из всех
, состоящая из всех  функций этого класса. Т.к. любая ФАЛ может быть представлена в СНДФ или СНКФ, то, следовательно, будет верным и утверждение о полноте системы, состоящей из трех функций: отрицания, конъюнкции, и дизъюнкции.
функций этого класса. Т.к. любая ФАЛ может быть представлена в СНДФ или СНКФ, то, следовательно, будет верным и утверждение о полноте системы, состоящей из трех функций: отрицания, конъюнкции, и дизъюнкции.
Воcпользовавшись правилом де-Моргана:  и
и  видим, что в СНДФ и СНКФ можно заменить конъюнкцию (&) через отрицание (ù) и дизъюнкцию (Ú), или дизъюнкцию через конъюнкцию и отрицание. Т.е. базисы { &, ù } и {Ú, ù} являются минимальными.
видим, что в СНДФ и СНКФ можно заменить конъюнкцию (&) через отрицание (ù) и дизъюнкцию (Ú), или дизъюнкцию через конъюнкцию и отрицание. Т.е. базисы { &, ù } и {Ú, ù} являются минимальными.
Из того факта, что всякая ФАЛ представима в СНПФ следует, что базис {&, Å, ù } является полным. Из этой системы можно исключить отрицание, т.к.  . Если в СНПФ произвести такую замену, то получим представление функции через { Å, &, 1}. Такое представление носит название полинома Жегалкина (полином по Å).
. Если в СНПФ произвести такую замену, то получим представление функции через { Å, &, 1}. Такое представление носит название полинома Жегалкина (полином по Å).
Аналогично, из соотношений 1.27 и 1.33 следует, что полную систему функций образуют {ù, &, º }. Кроме того, из последней системы можно исключить конъюнкцию (&), (т.к.  ), а отрицание выразить через импликацию и константу нуля (
), а отрицание выразить через импликацию и константу нуля ( ). Т.е. { ®, 0 } также образуют базис.
). Т.е. { ®, 0 } также образуют базис.
Теорема 1.7 Функция Шеффера образует в  полную систему.
полную систему.
Доказательство:
Имеем:  ;
;  .
.
Т.к. отрицание и конъюнкция образуют в множестве  полную систему, следовательно и функция Шеффера образует полную систему.
полную систему, следовательно и функция Шеффера образует полную систему.
Теорема 1.8 Функция Пирса (Вебба) образует в  полную систему.
полную систему.
Доказательство:
Имеем:  ;
;  .
.
А так как отрицание и дизъюнкция образуют полную систему, следовательно и функция Пирса образует полную систему.
Теорема Поста-Яблонского (без доказательства) Для того чтобы система ФАЛ была полной, необходимо и достаточно, чтобы она содержала хотя бы одну функцию:
· не сохраняющую нуль;
· не сохраняющую единицу;
· не являющейся линейной;
· не являющейся монотонной;
· не являющейся самодвойственной.
Применим теорему для доказательства, например, полноты системы функций {ù, Ú }. Функция ù (отрицание) не сохраняет константы нуля и единицы и не является монотонной. Функция Ú (дизъюнкция) не является самодвойственной и линейной.
В таблице 1.2 приведена принадлежность элементарных функций тому или иному из классов, используемых в теореме Поста-Яблонского.
Таблица 1.2
| ФАЛ | 
| класс | |||||||
 
| 
| L | M | S | |||||
| f º0 | + | + | + | ||||||
f = 
| + | + | + | ||||||
f = 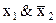
| + | ||||||||
f = 
| + | + | + | + | + | ||||
f = 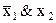
| + | ||||||||
f = 
| + | + | + | + | |||||
f = 
| + | + | |||||||
f = 
| + | + | + | ||||||
f = 
| |||||||||
f = 
| + | + | |||||||
f = 
| + | + | |||||||
f = 
| + | ||||||||
f = 
| + | ||||||||
f = 
| + | + | |||||||
f = 
| |||||||||
| f º1 | + | + |
Глава 2
Минимизация ФАЛ
Минимальная форма представления ФАЛ есть такая форма представления, которая содержит минимальное количество термов и переменных в термах. Минимальная форма представления ФАЛ не допускает никаких упрощений.
Пусть задана СНДФ:

 ;
;
Т.к. xÚx=x, то
 Ú
Ú
 Ú
Ú  .
.
Теперь преобразуем это выражение, используя распределительный и сочетательный законы для конъюнкции и дизъюнкции, и используя также аксиому  . Получаем:
. Получаем:
 =
= 
 =
= 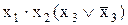 Ú
Ú  Ú
Ú
Ú 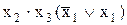 =
=  =
=  Ú
Ú
 =
= 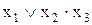 .
.
Как видно, результат преобразований позволил существенно упростить заданную ФАЛ.
Определение. Конъюнкция  называется элементарной, если в этой конъюнкции каждая переменная встречается не более одного раза.
называется элементарной, если в этой конъюнкции каждая переменная встречается не более одного раза.
Определение. Дизъюнкция элементарных конъюнкций называется дизьюнктивной нормальной формой (ДНФ или НДФ).
Определение. Длиной ДНФ называется число элементарных конъюнкций, образующих эту ДНФ.
Определение. Дизъюнктивная нормальная форма, имеющая наименьшую длину по сравнению со всеми другими ДНФ, эквивалентными данной функции, называется кратчайшей ДНФ
2.1 Числовое и геометрическое представление ФАЛ.
Для упрощения записи ФАЛ вместо полного перечисления термов используют номера наборов, для которых функция принимает единичное значение. Например, функция, заданная в таблице 1.5.1 может быть задана как
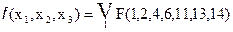 .
.
Это значит, что данная функция принимает значение логической единицы на наборах, номера которых равны 1, 2, 4, 6, 11, 13, 14. Такую форму записи называют числовой или числовой формой представленияФАЛ.
Функцию двух переменных можно интерпретировать как некоторую плоскость, заданную в системе координат  -
-  . Отложив на осях единичные отрезки, получим квадрат, вершины которого соответствуют комбинациям логических переменных
. Отложив на осях единичные отрезки, получим квадрат, вершины которого соответствуют комбинациям логических переменных 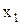 и
и 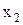 . Это проиллюстрировано на рис.2.1.
. Это проиллюстрировано на рис.2.1.

Рис. 2.1
Из такого геометрического представления функций двух переменных следует: две вершины, принадлежащие одному и тому же ребру и называемые соседними, “склеиваются” по переменной, меняющейся вдоль этого ребра.
Геометрическое представление для функций трех переменных можно выполнить в виде куба (рис. 2.2) Вполне очевидно, что ребра куба поглощают вершины. Грани куба поглощают свои ребра и, следовательно, вершины.

Рис. 2.2
Функция четырех переменных представляется уже в виде “четырехмерного” куба, как это приведено на рис. 2.3.
В геометрическом смысле каждый набор 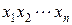 может рассматриваться как n-мерный вектор, определяющий точку n-мерного пространства. Координаты вершин куба должны быть указаны в порядке, соответствующем порядку перечисления переменных в записи функции. Отметив точками (крестиками или другими символами) вершины, в которых функция принимает значение, равное единице, получим геометрическое представление ФАЛ
может рассматриваться как n-мерный вектор, определяющий точку n-мерного пространства. Координаты вершин куба должны быть указаны в порядке, соответствующем порядку перечисления переменных в записи функции. Отметив точками (крестиками или другими символами) вершины, в которых функция принимает значение, равное единице, получим геометрическое представление ФАЛ
 |
Рис. 2.3
Терм максимального ранга принято называть 0-кубом (точкой) и обозначать  . Например, для
. Например, для 

Если два 0-куба из комплекса  различаются только по одной переменной (координате), то они образуют 1-куб (отрезок) -
различаются только по одной переменной (координате), то они образуют 1-куб (отрезок) -  .
.
 ={ 0 x 0}, где x - независимая переменная.
={ 0 x 0}, где x - независимая переменная.
Если два 1-куба имеют общую независимую компоненту и различаются только по одной координате, то они образуют 2-куб. ( )
)
Таким образом, для построения одномерного единичного куба берут два 0-куба (точки) и соединяют отрезком прямой. Двумерный куб (грань) получается, если вершины двух 1-кубов соединить параллельными отрезками Трехмерный куб получается при соединении соответствующих вершин двух двумерных кубов отрезком единичной длины. Геометрическое представление используется при разработке методов минимизации с использованием минимизирующих карт.