Метод неопределенных коэффициентов

Описываемый здесь метод может быть применим для минимизации ФАЛ от любого числа аргументов, однако для простоты изложения и большой наглядности его рассмотрение произведем на примере минимизации функции, зависящей от трех переменных.

Представим в ДНФ.

=

,

т.е. здесь представлены все возможные конъюктивные члены, которые могут входить в ДФ. Коэффициенты K с различными индексами являются неопределенными и подбираются так, чтобы получающаяся после этого дизъюнктивная форма была минимальной. {K=0,1}. Критерий минимальности - минимальное количество символов в записи ДНФ. При записи ДНФ пользуются следующими свойствами:

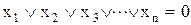· если ;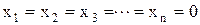

· если хотя бы один член равен 1.

Если теперь задавать всевозможные наборы значений аргументов 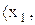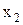, и приравнять после этого выражение (отбрасывая нулевые конъюнкции) значению функции на выбранных наборах, то получим систему уравнений:

Если =0, то все коэффициенты, входящие в данное уравнение равны 0, тогда и в остальных уравнениях системы надо вычеркнуть члены, содержащие нулевые коэффициенты, а из оставшихся уравнений, равных единице, найти коэффициенты, определяющие конъюнкцию наименьшего ранга в каждом из уравнений.

На основании изложенного можно сформулировать алгоритм нахождения неопределенных коэффициентов:

1. Выбрать очередную строку, в которой =0. Все коэффициенты этой строки приравнять нулю;

2. Если все нулевые строки просмотрены, то перейти к п.3, если нет, то к п.1;

3. Просмотреть строки, в которых =1, и вычеркнуть из них все коэффициенты, встречающиеся в строках, где =0;

4. Переписать все модифицированные уравнения;

5. Выбрать очередную строку =1 и вычеркнуть максимально возможное количество коэффициентов так, чтобы ранг остающихся членов был минимальным.

Следует заметить, что метод неопределенных коэффициентов применим для дизъюнктивной формы и практически непригоден для конъюктивной формы.

Пример. Минимизировать функцию: .

Запишем данную функцию в дизъюнктивной форме:

.

Составим систему уравнений:

Отсюда вытекает, что

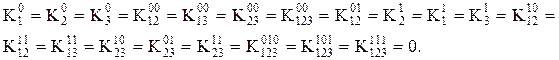
После вычеркивания нулевых коэффициентов уравнения принимаю вид:

И вполне очевидно, что из этих уравнений следует:

И тогда получаем: .

Метод Квайна

При минимизации по методу Квайна предполагается, что минимизируемая ФАЛ задана в СНДФ. Сам метод Квайна предполагает последовательное выполнение следующих этапов:

1. Нахождение первичных импликант.

Импликанта функции - некоторая логическая функция, обращаемая в нуль при наборе переменных, на которых сама функция также равна нулю.

Первичная импликанта функции - импликанта типа элементарной конъюнкции некоторых переменных, никакая часть которой уже не является импликантой.

Все минтермы (минитермы) данной функции сравнивают между собой попарно. Если минтермы и таковы, что они имеют вид и , то выписывается конъюнкция f (), являющаяся минтермом (n-1)-го ранга.

Минтермы n-го ранга, для которых произошло склеивание, отмечаются. После построения минтермов (n-1)-го ранга вновь сравнивают их попарно, выписывают минтермы (n-2)-го ранга и отмечают минтермы (n-1)-го ранга, подвергшиеся склеиванию, и т.д. Процесс заканчивается, когда минтермы полученного ранга уже не склеиваются между собой. Все отмеченные минтермы называются первичными или простыми импликантами.

Пример. Минимизировать методом Квайна ФАЛ:

.

Запишем данную функцию в СНДФ:

=

Исходный минтерм

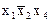
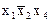
Первичн. импл. 3-го ранга

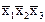
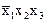
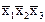
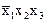
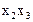
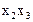
Итак, получаем импликанты наименьшего ранга .

2. Расстановка меток

Составляется таблица, число меток которой равно числу полученных первичных импликант, а число столбцов совпадает с числом минтермов СНДФ. Если в некоторый минтерм СНДФ входит какая-либо из первичных импликант, то на пересечении соответствующего столбца и строки ставится метка.

Первичн.	Исходные термы
импли-
канты
	+	+
		+			+
					+	+
				+				+
						+		+
			+	+			+	+

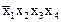
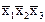
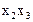
3. Нахождение существенных импликант

Если в каком либо из столбцов имеется только одна метка, то первичная импликанта в соответствующей строке является существенной, т.к. без нее не будет получено все множество заданных минтермов. В данном примере это импликанты 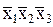и .

Столбцы, соответствующие существенным импликантам, из таблицы вычеркиваются. В данном примере это 1, 2, 3, 4, 7, и 8 столбцы.