Минимизация не полностью определенных функций

 

Основная задача минимизации не полностью определенных функций заключается в отыскании оптимального варианта ее доопределения, позволяющего получить минимальную из всех возможных ДНФ или КНФ. Если значения функции не заданы в m точках, то ее можно доопределить способами. СНДФ не полностью определенной функции можно представить в виде:

= ,

где , - номера наборов, при которых функция определена и равна ”1”; 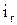- номера наборов при которых функция имеет не доопределенное значение (f =F).

Пример. Пусть необходимо минимизировать не полностью определенную ФАЛ, имеющей вид: .

Для данной функции имеем следующую карту Карно:

`

И тогда доопределяя карту Карно (а равно и функцию) получаем следующую минимизированную функцию:

или

Глава 3

Приложения алгебры логики

 

3.1. Логические элементы и их применение

 

Одним из самых широких приложений алгебры логики является разработка дискретных, цифровых устройств различного назначения и, в частности, средств вычислительной техники.

Техническим аналогом элементарных логических функций являются логические элементы (ЛЭ), представляющие собой физические устройства, выполняющие логические операции над сигналами, представленными в физической форме. Т.е. в этих устройствах логические единица и нуль представлены физическими сигналами различной величины, одна из величин соответствует логической единице, другая – логическому нулю. Например, различные величины давления: р₁ и р₂ (пневматические или гидравлические логические элементы); различные величины интенсивности освещения: s₁, s₂ (оптические или оптоэлектронные логические элементы). Но доминирующее значение в технике имеют электронные логические элементы, которые представляют собой определенные электронные схемы, реализующие логические операции над логическими переменными, представленными в этом случае в виде электрических сигналов. Имеет место несколько способов представления логических единицы и нуля в виде электрических сигналов, но преимущественно используется потенциальный способ представления логических переменных, при котором значениям логической единицы и нуля соответствуют вполне определенные уровни напряжения: U¹ и U⁰. Потенциальные логические элементы (схемы) в настоящее время составляют основу системы изделий микроэлектроники для цифровой, вычислительной техники. Они представлены в виде серии микросхем различных степеней интеграции, предназначенных для построения цифровых устройств различного назначения, и в частности – ЭВМ различных классов.

По виду реализуемой логической функции основные логические элементы условно разделяют на элементы одноступенчатой логики, реализующие функции И (конъюнкция), ИЛИ (дизъюнкция), НЕ (отрицание), И-НЕ, ИЛИ-НЕ, и на элементы двухступенчатой логики, реализующие функции И-ИЛИ, ИЛИ-И, И-ИЛИ-НЕ, ИЛИ-И-НЕ, И-ИЛИ и т.п.

Число входов ЛЭ соответствует числу входных переменных, воспроизводимой им логической функции.

На основании вышеизложенного вполне очевидно, что любой функции алгебры логики можно сопоставить соответствующую логическую схему, составленную из соответствующих логических элементов.

Схема, значение выходного сигнала которой определяется только комбинацией входного сигнала, называется комбинационной.

Для набора логических элементов можно ввести понятие функциональной полноты, подобно тому, как это было сделано для случая ФАЛ. Набор ЛЭ обладает функциональной полнотой, если с помощью этого набора можно реализовать схему с любым законом функционирования.

Т.е. любая комбинационная схема может быть построена с применением логических элементов типа И, ИЛИ, НЕ, совокупность которых является функционально полной системой (т.е. базисом), а также и из элементов типа И-НЕ (функция ), или из элементов типа ИЛИ-НЕ (функция ), или из элементов типа И-ИЛИ-НЕ (функция ), каждая из которых представляет функционально полною систему.

Принятые условные обозначения некоторых основных ЛЭ приведены в таблице 3.1.

Промышленно выпускаемые логические элементы имеют ограниченное количество входов (коэффициент разветвления по входу в большинстве случаев равен 2, 3, 4, 8) и ограниченную нагрузочную способность. Но имеются известные схемотехнические решения увеличения коэффициента разветвления по входу и выходу, и которые, к сожалению, увеличивают и логическую глубину схемы, тем самым ухудшая временные и другие характеристики схемы в целом.

Практическая реализация логических схем осуществляется, как правило, с применением интегральной схемотехники, среди которой наиболее широкое распространение получили элементы потенциального типа, логические переменные 0 и 1 в которых, как уже отмечалось, отображаются двумя уровнями напряжения: U⁰ и U¹ соответственно. Для логического описания цепей не требуются абсолютные значения U⁰ и U¹. Необходимо лишь условиться, какой из них отображает логический нуль и какой - логическую единицу.

 

Таблица 3.1

Тип логического элемента	Обозначение	Выполняемая функция
И		конъюнкция
ИЛИ	X1 X2 X1ÚX2Ú…Xn   Xn	дизъюнкция
НЕ	X X	отрицание
&   И-НЕ	X1 X2 X1X2….Xn   Xn	Отрицание конъюнкции
ИЛИ-НЕ	X1 X2 X1ÚX2Ú…Xn   Xn	Отрицание дизъюнкции
И-ИЛИ-НЕ	X1 & 1 X2 Xn X1X2…XnÚZ1…Zk Z1 & Z2   Zk	Отрицание дизьюнкции коньюнкций

 

 

Возможно два варианта представления логических переменных с помощью двух уровней напряжения. В первом варианте за 1 принимается высокий уровень напряжения, обозначаемый латинской буквой H (от англ. high). Во втором варианте логическая единица отображается низким уровнем напряжения - L (от англ. low). Первый вариант называют соглашением положительной логики (U⁰ < U¹), второй - соглашением отрицательной логики (U⁰ > U¹).

Изменение способа представления переменных ведет к изменению логической функции, выполняемой данным элементом (принцип двойственности). Например, пусть имеется элемент, функционирующий следующим образом:

 

Х1	Х2	Y
L	L	L
L	H	L
H	L	L
H	H	H

 

где Х₁ и Х₂ - входные сигналы, Y - выходной сигнал

Приняв положение положительной и отрицательной логики, соответственно получаем:

Положительная логика: L=”0”, H=”1”.

 

Х1	Х2	Y

 

Согласно определению, видно, что в данном случае элемент выполняет операцию И

Отрицательная логика: L=”1”, H=”0”.

 

Х1	Х2	Y

 

 

В этом случае элемент, как видно, выполняет операцию ИЛИ.

Т.е. для операцииИ в положительной логике имеем Y=Х₁×Х₂. Инвертируя все переменные получаем:

Преобразуя это выражение по правилу де Моргана имеем: Y=Х₁vХ₂, т.е. для отрицательной логики этот элемент выполняет операцию ИЛИ.

Правило соответствия для основных операций и соглашений положительной и отрицательной логики имеет вид:

И«ИЛИ; И-НЕ«ИЛИ-НЕ; М₂«М_2.

При разработке логических комбинационных схем возникает проблема простейшего представления соответствующих им логических функций, которая сводится к проблеме выбора базиса и проблеме более экономного представления функции в этом базисе. В настоящее время существенные результаты в решении задач минимизации получены лишь для базиса, состоящего из отрицания, конъюнкции и дизъюнкции. Минимизация логических функций в зависимости от их сложности и формы представления может производиться различными методами, например, непосредственно с использованием теорем и свойств АЛ, с помощью карт Карно, методом неопределенных коэффициентов, методом Квайна – Мак-Класски, и т.д.

В интегральной схемотехнике наиболее применяются элементы и устройства реализуемые в базисе И-НЕ или в базисе ИЛИ-НЕ, которые представляют, как уже отмечалось, функционально полный базис, т.е. позволяют реализовать любую логическую функцию:

Рис.3.1

Реализация элементов основного базиса на элементах И-НЕ

а) инвертор б) дизъюнкция в) конъюнкция

 

Действительно, в базисе И-НЕ имеем:

а) ,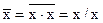

т.е. инвертор реализуется элементом И-НЕ с запараллеленными входами (рис.3.1 а);

б) ,

т.е. дизъюнктор реализуется тремя элементами И-НЕ (рис.3.1 б);

в) ,

т.е. конъюнктор реализуется двумя элементами Шеффера (рис.3.1 в).

 

В базисе ИЛИ-НЕ:

а) ,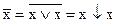

т.е. инвертор реализуется элементом ИЛИ-НЕ с запараллеленными входами

(рис. 3.2 а);

б) ,

т.е. дизъюнктор реализуется двумя элементами ИЛИ-НЕ (рис. 3.2 в);

в)

т.е. конъюнктор реализуется тремя элементами ИЛИ-НЕ (рис. 3.2 б);

Рис.3.2

Реализация элементов основного базиса на элементах ИЛИ-НЕ

а) инвертор б) конъюнктор в) дизъюнктор

 

Таким образом, все основные операции (НЕ, И, ИЛИ) могут быть реализованы на элементах любого из рассмотренных базисов.

Рассмотрим пример схемной реализации логической функции, заданной табличным методом:

Х1	Х2	Х3	Х4	Y

В СНДФ функция будет иметь вид:

Минимизируем данную функцию с помощью карты Карно:

 

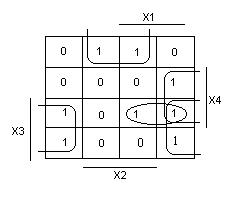
получаем:

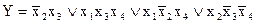
Реализуем данную функцию в базисе И-НЕ:

Из последнего выражения видно, что для реализации данной функции необходимо иметь 3 элемента типа 3И-НЕ, 1 элемент типа 2И-НЕ, 1 элемент типа 4И-НЕ и 3 элемента типа НЕ.

 

Рис.3.3

На рисунке 3.3 приведена соответствующая логическая схема, реализующая заданную функцию в базисе элементов И-НЕ.

Аналогично можно данную функцию реализовать и в других элементных базисах.

 

Триггеры

 

Еще одним важнейшим элементом цифровых устройств, являющимся основополагающим, так сказать – «атомарным», является триггер.

Триггер - функциональное устройство с двумя устойчивыми состояниями выхода, содержащее элементарную запоминающую ячейку и схему управления, преобразующую поступающую информацию в комбинацию сигналов, действующих непосредственно на входы элементарной запоминающей ячейки.

Применение триггеров: счетчики, делители частоты, пересчетные устройства, регистры, накапливающие сумматоры, устройства управления, формирователи импульсов и т.д., т.е. триггер является фундаментальным элементом средств цифровой техники. Другими словами-триггер является простейшим, элементарным цифровым автоматом, обладающий памятью и служащий для хранения одного бита информации. Триггер, как конечный автомат характеризуется следующими свойствами:

1. Возможное число внутренних состояний - два, это логические “0” и “1”, что соответствует одной внутренней переменной Z, обозначаемой для триггеров обычно буквой Q.

2. Число выходных переменных y - одно; значение переменной y совпадает со значением Q, т.е. , поэтому триггер является автоматом Мура.

3. Число переменных x зависит от типа триггера.

Наряду с выходом Q, называемым прямым, триггер имеет, как правило, другой (инверсный) выход .