Функции алгебры логики и их основные свойства.

1.1 Основные определения

Для формального описания цифровых автоматов(ЦА) широко применяют аппарат алгебры логики (АЛ), являющейся одним из разделов математической логики. Создатель алгебры логики - английский математик Джордж Буль (1815 - 1864).

Определение 1. Основное понятие АЛ - высказывание. Высказывание - некоторое предложение, о котором можно утверждать, что оно истинно или ложно. Любое высказывание можно обозначить символом, например, X и считать, что X=1, если высказывание истинно, X=0 если высказывание ложно.

Определение 2. Логическая (Булева) переменная - такая величина X, которая может принимать только два значения: X = { 0, 1 }.

Определение 3. Высказывание абсолютно истинно, если соответствующая ей логическая величина X принимает единичное значение при любых условиях.

Определение 4. Высказывание абсолютно ложно, если соответствующая ей логическая переменная X принимает нулевое значение при всех условиях.

Логическая функция (функция алгебры логики - ФАЛ) - функция ¦ 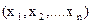, принимающая значение, равное нулю или единице на наборе логических переменных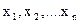

Рассмотрим множество векторов 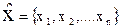, где 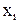- (координаты векторов) могут принимать значения 0 или 1. Таким образом, множество состоит из 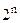различных векторов. Совокупность координат некоторого фиксированного вектора из множества 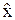будем называть двоичным набором. Сопоставим каждому вектору из 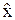число 0 и 1, т. е. произведем однозначное отображение множества 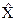на множество Y { 0, 1}.

Определение 5 Функцией алгебры логики (ФАЛ) называется функция, дающая однозначное отображение X в Y.

Т. к. число различных наборов значений аргументов является конечным, то любая ФАЛ может быть полностью задана конечной таблицей. В левой части этой таблицы перечислены все наборы значений аргументов этой функции, а в правой части - значения функции на этих наборах.

Логические переменные	Функция
		...	...	...	...			¦
		...	...	...	...
		...	...	...	...	...
...	...	...	...	...	...	...	...	...
		...	...	...	...
...	...	...	...	...	...	...	...	...

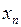
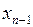
Определение 6. Если две ФАЛ ¦ 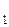(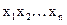) и ¦ 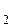(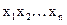) принимают на всех возможных наборах значений аргументов одинаковые значения, то функци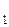и ¦ и ¦ 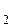называются равносильными или равными, т.е.:

¦ () = ¦ ()

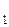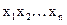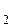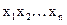Определение 7. Функция ¦ () существенно зависит от аргумента , если имеет место соотношение:

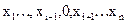¦ () ¹ ¦ ()

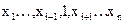В противном случае говорят, что от функция зависит несущественно и является фиктивным аргументом. ФАЛ не изменится, если к ее аргументам дописать любое число фиктивных аргументов, или зачеркнуть все фиктивные аргументы.

Теорема 1.1 Число различных ФАЛ, зависящих от n аргументов конечно и равно .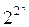

Для доказательства составим таблицу:

0 0... 0 0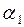
0 0... 0 1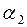
0 0... 1 0
...	...
1 1... 1 1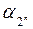

В этой таблице справа стоит одна из ФАЛ, зависящая от n аргументов. Задавая тот или иной конкретный двоичный набор < >, мы будем тем самым задавать одну из возможных функций алгебры логики. Но различное число таких наборов равно 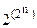. Теорема доказана.

Значения функции могут быть заданы не на всех возможных наборах аргументов. На некоторых наборах значения ФАЛ могут быть не определены. Такие ФАЛ называют не полностью определенными или не- доопределенными. Функцию можно доопределить. Если ФАЛ не определена на m наборах аргументов, то путем ее произвольного доопределения можно получить 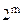различных полностью определенных функций.