Координаты векторов; линейные операции над векторами, заданными координатами.

Линейные операции над векторами, заданными координатами. Декартова система координат. Деление отрезка в данном отношении.

Свойства: 1) Каждый вектор коллинеарный какой-либо прямой может быть разложен по базису на этой прямой. 2) Каждый вектор || плоскости может быть разложен по базису этой плоскости. 3) Каждый вектор может быть разложен по базису в R. Компоненты и координаты в каждом случае определяются однозначно.

Декартовой системой координат (ДСК) в пространстве называется совокупность точки и базиса. ДСК, базис которой ортонормирован, называется декартовой прямоугольной системой координат. Векторы будут образовывать правую тройку, если из конца вектора с кратчайший поворот от вектора а к b виден против часовой стрелки.

Деление отрезка в заданном отношении. Разделить отрезок в отношении λ (λ≠1) — это значит, на прямой, проходящей через т. А и В, найти т. С, что АС = λ СВ.

Разложение вектора по базису. Если дана упорядоченная тройка векторов (a,b,c) некомпланарных векторов, то для любого вектора p существует единственная упорядоченная тройка чисел (x,y,z), удовлетворяющая равенству p=xa+yb+zc.

Скалярное произведение векторов.

Скалярным произведением вект. А и В называется число, равное произведению длин этих векторов, умноженному на косинус угла между ними

Свойства. 1) (a,b)=(b,a) (коммутативность). 2) (λa,b) =(a, λb) = λ (a,b) (ассоциативность). 3) дистрибутивно относительно сумсуммы (а+b,с)=(а,b)+(а,с) 4) Скалярное произведение двух векторов равно нулю тогда и только тогда когда хотя бы один из вект. нулевой либо они перпендикулярны (a • b = 0, если a ┴ b).

Скалярным квадратом называется скалярное произведение вектора на себя => равен квадрату длины вектора.

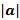(a,b)= *|b|*Cos(a^b); пр_ab=(a,b)/ (проекция a на b). Длина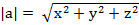

Скалярное произведение в коорд форме. Коорд орты i,j,k имеют длины, равные единицы i²=j²=k²=1, их взаимное произведение равно 0. (a,b) =a_x*b_x+a_y*b_y+a_z*b_z. Cos и ПР находятся с помощью координат.

Векторное произведение векторов.
Векторным произведением вектора а на вектор b называется вектор с, который: 1) Перпендикулярен векторам a и b, т. е. с^а и с^b; 2) Имеет длину, численно равную площади параллелограмма, построенного на векторах а и b как на сторонах, т. е. 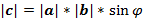. 3.Векторы a, b и с образуют правую тройку.

Свойства: 1. При перестановке сомножителей векторное произведение меняет знак, т.е. [а,b] =[b,a]; 2. Векторное произведение обладает сочетательным свойством относительно скалярного множителя, т. е. [а,b] = [а,b] = [b,a]; 3. Два ненулевых вектора а и b коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору, т. е. а||b <=>[а,b] =0. 4.распределительное свойство:[a+b,с]= [ а,с]+[b,с].

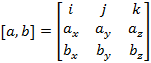
Числа называют координатами вектора в базисе 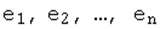и обозначают 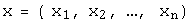. При этом для любых двух произвольных векторов 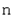-мерного линейного пространства 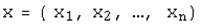, 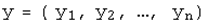и произвольного числа 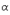справедливо: 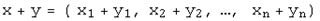и .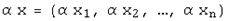

Это означает, что все 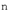-мерные линейные пространства “устроены” одинаково -- как пространство 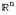векторов-столбцов из 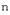действительных чисел, т.е. что все они изоморфны пространству .

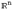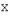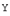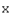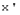Линейные пространства и называются изоморфными, если между их элементами можно установить такое взаимно однозначное соответствие, что если векторам и из 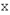соответствуют векторы и из 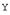, то вектору 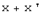соответствует вектор 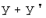и при любом 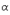вектору 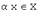соответствует вектор .

Изоморфизм 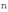-мерных линейных пространств пространству 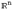означает, что соотношения между элементами 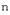-мерного линейного пространства и операции с ними можно изучать как соотношения между векторами из 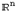и операции с ними и что всякое утверждение относительно векторов из 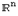справедливо для соответствующих элементов любого 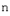-мерного линейного пространства.