Матрицы. Общие понятия и определения.

Матрицы. Общие понятия и определения

Матрицей размера называется прямоугольная таблица, содержащая чисел, состоящая из строк и столбцов.

Обозначение

Таблица берется либо в круглые скобки, либо окружается двумя параллельными вертикальными прямыми.

Если матрица содержит строк и столбцов, то матрица называется матрицей размера или -матрицей. Размер матрицы указывается справа внизу возле ее имени, либо таблицы с обозначением элементов.

Элементы матрицы

Элементы матрицы обозначаются , где - номер строки, в которой находится элемент, а - номер столбца.

Определение

Строка матрицы называется нулевой, если все ее элементы равны нулю. Если хотя бы один из элементов строки не равен нулю, то строка называется ненулевой.

Замечание. Аналогичное определение и для нулевого и ненулевого столбцов матрицы.

Диагонали

Определение

Главной диагональю матрицы называется диагональ, проведённая из левого верхнего угла матрицы в правый нижний.

Побочной диагональю матрицы называется диагональ, проведённая из левого нижнего угла матрицы в правый верхний.

Равенство матриц; сложение матриц; умножение матрицы на число; транспонирование матриц.

3.Транспонирование матрицы- переход от матрицы А к матрице А^/, в кот строки и столбцы поменялись местами с сохранением порядка. Матрица А^/ наз транспонированной относительно матрицы А. Св-ва: 1) (А^/)^/=А, 2) (λА^/)^/=λА^/, 3) (А+В)^/=А^/+В^/.4) (АВ)^/=А^/В^/.

1. Умножение матрицы на число. Произведением матрицы А на число λ наз матрица В=λА, элементы кот b_ij=λa_ij для i=1,2,…,m; j=1,2,…,n. Общий множитель всех элементов матрицы можно выносить за знак матрицы. Произведение матрицы А на число 0, равно нулевой матрице. (0А=0).

2. сложение матриц. Суммой двух матриц А и В одинакового размера m×n наз матрица С=А+В, элементы кот c_ij=a_ij+b_ij для i=1,2,…,m; j=1,2,…,n. (т е матрицы складываются поэлементно). В частности А+0=А.

4.Две матрицы А и В одного размера наз равными, если они совпадают поэлементно, т е a_ij=b_ij для любых i=1,2,…m; j= 1,2,…,n.

Определитель квадратной матрицы. Вырожденные и невырожденные матрицы.

Если кол-во строк= кол-ву столбцов, то такая матрица наз квадратной размером m×m(матрица порядка m). Понятие определитель приминяется только для квадратных матриц, detA,(А),∆. Определителем кв матрицы А наз число, кот вычисляется по след правилам: 1) А=(а₁₁) detA=а_11. 2) А=(а₁₁а₁₂) detA=а₁₁а₂₂-а₁₂а_21.

(а₂₁а₂₂)

3) А=(а₁₁а₁₂а₁₃)

(а₂₁а₂₂а₂₃)

(а₃₁а₃₂а₃₃)

Для 3) правилом ∆(Саррюса). detA=а₁₁а₂₂а₃₃+а₁₃а₂₁а₃₂+а₃₁а₁₂а₂₃-а₃₁а₂₂а₁₃-а₁₁а₃₂а₂₃-а₃₃а₂₁а_12.

4) Определитель п -го порядка – сумме произведения элементов какой-либо строки или столбца на их алгебраические дополнения. ∆=а_i1A_i1+a_i2A_i2+…+a_inA_in. –разложение по строке. ∆=a_ijA_1j+a_2jA_2j+…+a_njA_nj- разложение по столбцу.А_ij=(-1)^i+jM_ij- алгеброическое дополнение.

Умножение матриц.

Умножение матриц. Умножение матрицы А на матрицу В определено, если число столбцов матрицы А равно числу строк матрицы В. Произведением матрицы А размера m×k на матрицу В размера k×n наз матрица С размера m×n, каждый элемент кот = сумме произведений элементов i-строки матрицы А на соответствующие элементы j-столбца матрицы В. c_ij=a_i1b_1j+a_i2b_2j+…+a_ikb_ik.

7.Обратная матрица и ее вычисление.

Решить систему линейных уравнений с квадратной матрицей коэффициентов можно и другим способом, используя обратную матрицу. При этом определитель матрицы коэффициентов должен быть также отличен от нуля.
Рассмотрим квадратную матрицу:

Вырожденной (особенной) называется квадратная матрица, если ее определитель равен нулю, и невырожденной (неособенной) – в противном случае.
Обратной для матрицы называется матрица если выполняется:

где
единичная матрица.

Для вырожденной матрицы обратной матрицы не существует.
Обратную матрицу можно вычислить разными способами.
А) Одно из правил вычисления обратной матрицы:
берется невырожденная матрица
обратная матрица находится по формуле

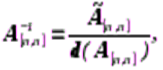
где присоединенная (или взаимная) матрица, состоящая из алгебраических дополнений элементов матрицы , где - минор порядка матрицы , получаемый из определителя матрицы вычеркиванием -ой строки и -ого столбца.
Обратим внимание, что в присоединенной матрице строки транспонированы в столбцы.