однополосный гиперболоид x2/a2 + y2/b2 - z2/c2 =1 a>0,b>0,c>0; Пересек. координатные осиплоскостями x=0,y=0,z=0 по гиперболам y2/b2 – z2/c2 = 1 x2/a2 – z2/c2=1 и эллипсоид x2/a2 + y2/b2 =1 соответственно. В сечениях однополосного гиперболоида плоскостями z=h всегда получаются эллипсы x2/a2 + y2/b2 = 1 + h2/c2 с полуосями 
и 
.
Каноническое уравнение: 
a = b - однополостный гиперболоид вращения вокруг оси Oz.
Горловой эллипс: 
Асимптотический конус: 
Сечения однополостного гиперболоида плоскостями - либо эллипс, либо парабола, либо гипербола, либо пара прямых (прямолинейных образующих).
Прямолинейные образующие
Через произвольную точку 
проходят две прямолинейные образующие с направляющими векторами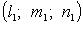 
и 
где:
В частности, если точку 
выбирать на горловом эллипсе 
то уравнениями прямолинейных образующих будут:
Двуполостный гиперболоид, его каноническое уравнение.
двуполостный гиперболоид x2/a2 - y2/b2 - z2/c2 =1 a>0,b>0,c>0; x=h получается эллипс x2/a2 + z2/b2 = -1 + h2/c2 с полуосями b*Корень(h2/a2-1) и с*Корень(h2/a2-1). При h=a получим в сечении точки (±а,0,0) – вершины двуполостного. В сечениях координ пл. z=0 и y=0 получим гиперболы x2/a2 – y2/b2 =1 и x2/a2 – z2 /c2 =1 соответсвенно.
Каноническое уравнение: 
a = b - двуполостный гиперболоид вращения вокруг оси Oz.
Асимптотический конус: 
Сечения двуполостного гиперболоида плоскостями: либо эллипс, либо гипербола, либо парабола, либо точка, либо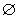 
.
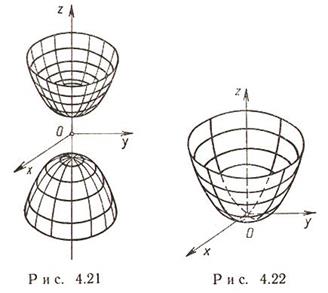
Эллиптический параболоид, его каноническое уравнение.
эллиптический параболоид x2/a2 + y2/b2=2pz a>0,b>0;
Каноническое уравнение: 
p = q - параболоид вращения вокруг оси Oz.
Сечения эллиптического параболоида плоскостями - либо эллипс, либо парабола, либо точка, либо .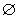 
Гиперболический параболоид, его каноническое уравнение. Семейства прямолинейных образующих гиперболического параболоида.
гиперболический параболоид x2/a2 - y2/b2=2pz a>0,b>0;
Каноническое уравнение:
Сечения гиперболического параболоида плоскостями - либо гипербола, либо парабола, либо пара прямых (прямолинейных образующих).
Прямолинейные образующие
Через каждую точку проходят две прямолинейные образующие:
 |
Поверхности вращения.
Поверхностью вращения называется поверхность, образованная вращением какой-либо плоской линии вокруг прямой, лежащей в плоскости этой линии.
Для вывода уравнения поверхности вращения необходимо выбрать систему координат. Чтобы уравнение поверхности вращения выглядело проще, ось вращения принимают за одну из координатных осей.
Пусть в координатной плоскости Oyz задана кривая L уравнением F(Y, Z)=0 (рис. 24). Вращаем кривую L вокруг оси Oy. Получим некоторую поверхность. Пусть M(x, y, z) - произвольная точка получившейся поверхности. Тогда 
, но 
т.к. если взять точку M1 с отрицательной аппликатой, то
Следовательно, имеем Y = y,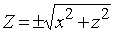 
и координаты точки M(x, y, z) удовлетворяют уравнению
Уравнение (62) и есть искомое уравнение поверхности вращения.
Т. о., чтобы получить уравнение поверхности, образованной вращением линии L, лежащей в плоскости Oyz, вокруг оси Oy, нужно в уравнении этой линии заменить z на 
Аналогичные правила будут иметь место и по отношению к уравнениям поверхностей, полученных вращением плоских линий вокруг других координатных осей.
Цилиндры.
цилиндры второго порядка: эллиптический цилиндр x2/a2 + y2/b2 = 1 a>0, b>0; гиперболический цилиндр x2/a2 - y2/b2 = 1 a>0, b>0; параболический цилиндр y2=2px; пара пересекающихся плоскостей a2x2-b2y2=0 a>0 b>0 пара параллельных или совпадающих плоскостей x-a=0 a>=0; прямая x2+y2=0
Конусы.
конус второго порядка x2/a2 - y2/b2 - z2/c2 =0 a>0,b>0,c>0; Пересекая пл. z=h -> x2/a2 + y2/b2 =1. В сечении плоскостями x=0 y=0 имеем пары пересек прямых y2/b2 - z2/c2 =0; x2/a2 - z2/c2 =0 соотв.
Линейные пространства