Матрица Линейного преобразования-мерного линейного пространства приводима к диагональному виду тогда и только тогда, когда существует базис этого пространства, состоящий из собственных векторов данного преобразования.
Любая квадратичная форма может быть приведена к каноническому виду при помощи некоторой линейной невырожденной замены переменных.
Квадратичные формы и их матрицы. Приведение квадратичной формы к каноническому виду ортогональным преобразованием. 
Квадратичная форма переменных 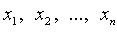 - функция
- функция
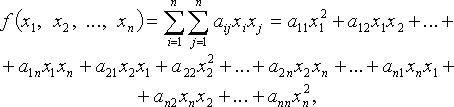
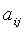 - коэффициенты квадратичной формы. Без ограничения общности считают
- коэффициенты квадратичной формы. Без ограничения общности считают  тогда
тогда
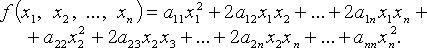
Если переменные 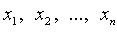 принимают действительные значения и
принимают действительные значения и 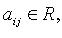 квадратичная форма называется действительной.
квадратичная форма называется действительной.
Матричная запись квадратичной формы
Матрица 
называется матрицей квадратичной формы, ее ранг - рангом квадратичной формы. Квадратичная форма называется невырожденной, если 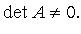
Главные миноры матрицы A называются главными минорами квадратичной формы.
В пространстве 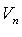 квадратичную форму можно записать в виде
квадратичную форму можно записать в виде 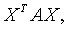 где X - координатный столбец вектора
где X - координатный столбец вектора 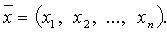
В пространстве  квадаратичную форму можно представить в виде
квадаратичную форму можно представить в виде 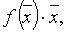 где f - линейный самосопряженный оператор, матрица которого в некотором ортонормированном базисе равна A.
где f - линейный самосопряженный оператор, матрица которого в некотором ортонормированном базисе равна A.
Пределы
Предел последовательности. Основные понятия и определения.
Определение. Число  называется пределом последовательности называется пределом последовательности 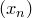 , если для любого положительного числа , если для любого положительного числа  найдется член последовательности такой, что все члены последовательности найдется член последовательности такой, что все члены последовательности 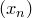 , следующие за ним, отстоят от , следующие за ним, отстоят от  меньше, чем на меньше, чем на  .
Определение. Число .
Определение. Число  называется пределом последовательности называется пределом последовательности 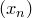 , если в любом открытом промежутке, содержащем число , если в любом открытом промежутке, содержащем число  , содержатся все члены последовательности , содержатся все члены последовательности 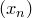 , начиная с некоторого.
Теорема (о единственности предела). Если , начиная с некоторого.
Теорема (о единственности предела). Если  — предел последовательности — предел последовательности  и и 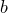 — предел последовательности — предел последовательности 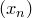 , то , то 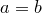 .
Доказательство.Предположим, что .
Доказательство.Предположим, что 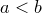 . Возьмем . Возьмем  . Найдется такой номер . Найдется такой номер 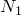 , что , что 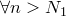
 также существует
также существует 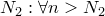
 Возьмем
Возьмем 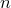 , которое больше , которое больше 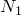 и и  . Тогда . Тогда
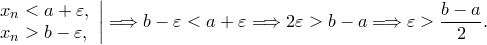 Обозначение.
Обозначение.  есть предел есть предел 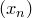 : :
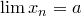 , ,
 — — 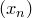 стремится (сходится) к стремится (сходится) к  , ,
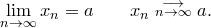 Определение. Последовательность, имеющая предел, называется сходящейся.
Определение. Последовательность называется строго возрастающей (возрастающей) [ строго убывающей ]
Определение. Последовательность, имеющая предел, называется сходящейся.
Определение. Последовательность называется строго возрастающей (возрастающей) [ строго убывающей ] 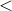 убывающей убывающей  , если каждый ее член, начиная со второго, больше (не меньше) [меньше] , если каждый ее член, начиная со второго, больше (не меньше) [меньше] 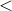 не больше не больше  предыдущего члена.
Последовательности (строго) возрастающая и (строго) убывающая называются (строго) монотонными.
Определение. Последовательность предыдущего члена.
Последовательности (строго) возрастающая и (строго) убывающая называются (строго) монотонными.
Определение. Последовательность 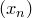 называется ограниченной, если существует называется ограниченной, если существует 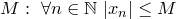 .
Теорема. Всякая сходящаяся последовательность ограничена.
Доказательство.Пусть .
Теорема. Всякая сходящаяся последовательность ограничена.
Доказательство.Пусть  — предел последовательности — предел последовательности 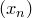 . Тогда найдется такой номер . Тогда найдется такой номер  , что , что 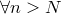 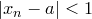
 Тогда
Тогда  .
Замечание. Тем самым, мы доказали ограниченность последовательности .
Замечание. Тем самым, мы доказали ограниченность последовательности  , поскольку, выбрав , поскольку, выбрав 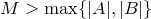 , получим , получим  .
Определение. Говорят, что последовательность .
Определение. Говорят, что последовательность 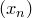 отделена от нуля, если найдется такое положительное число отделена от нуля, если найдется такое положительное число  , что все члены этой последовательности по модулю больше , что все члены этой последовательности по модулю больше  .
Теорема (о предельном переходе в неравенствах). Пусть .
Теорема (о предельном переходе в неравенствах). Пусть  и и 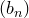 — последовательности, причем — последовательности, причем 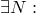 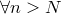  . Пусть . Пусть  , , 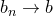 . Тогда . Тогда  .
Доказательство. Предположим, что утверждение теоремы неверно, т.е. .
Доказательство. Предположим, что утверждение теоремы неверно, т.е. 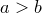 . Рассмотрим промежутки . Рассмотрим промежутки
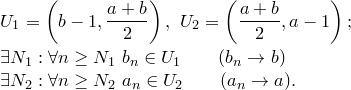 Возьмем
Возьмем 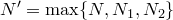 . Тогда . Тогда 
 Получили противоречие, т.к.
Получили противоречие, т.к.
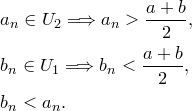 Замечание. Если в условии теоремы заменить неравенство
Замечание. Если в условии теоремы заменить неравенство  на на 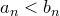 , то все равно можно утверждать лишь то, что , то все равно можно утверждать лишь то, что  . Действительно, . Действительно,
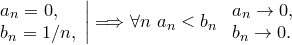 Теорема (принцип сжатой последовательности, теорема о двух милиционерах). Пусть даны последовательности
Теорема (принцип сжатой последовательности, теорема о двух милиционерах). Пусть даны последовательности 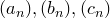 и существует и существует  : : 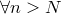 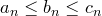 . Известно, что . Известно, что  . Тогда . Тогда 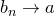 .
Доказательство.Возьмем произвольный промежуток .
Доказательство.Возьмем произвольный промежуток  . .
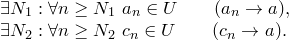 Обозначим
Обозначим 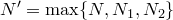 . Тогда . Тогда 
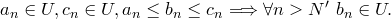 Значит,
Значит, 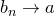 .
Замечание. Принцип сжатой последовательности является теоремой существования и не следует из теоремы о предельном переходе в неравенствах.
Определение. Говорят, что .
Замечание. Принцип сжатой последовательности является теоремой существования и не следует из теоремы о предельном переходе в неравенствах.
Определение. Говорят, что 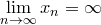 , если , если 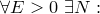
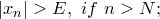 Последовательность
Последовательность 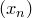 при этом называется бесконечно большой; при этом называется бесконечно большой;
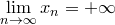 , если , если 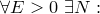

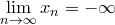 , если , если 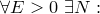
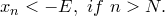 Определение. Последовательность
Определение. Последовательность 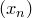 называется бесконечно малой, если называется бесконечно малой, если 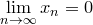 . .
|
61. Бесконечно малые последовательности и их свойства.
Ф-ция  называется бесконечно малой при
называется бесконечно малой при 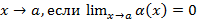
Другими словами, если 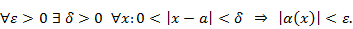
- Алгебраическая сумма бесконечно малых функций есть функция бесконечно малая.
Пусть 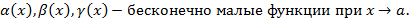
Из этого следует, что
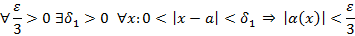
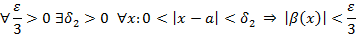
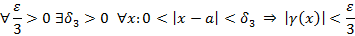
- Произведение бесконечно малой функции на ограниченную функцию есть величина бесконечно малая.
Пусть 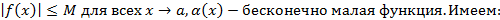
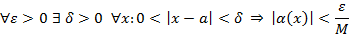
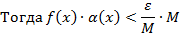
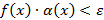
Следствия.
a) Произведение постоянной величины на бесконечно малую есть ф-ция бесконечно малая.
Пусть функция 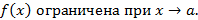 Тогда существует такое число
Тогда существует такое число  , что
, что
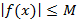
для всех 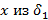 -окрестности точки х0. И пусть
-окрестности точки х0. И пусть  – бесконечно малая ф-ция, при
– бесконечно малая ф-ция, при 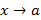 . Тогда для
. Тогда для  выполняется неравенство
выполняется неравенство 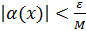
Следовательно, 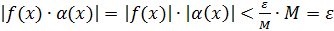 .
.
Это означает, что 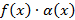 при
при 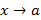 есть бесконечно малая ф-ция.
есть бесконечно малая ф-ция.
b) Произведение двух бесконечно малых есть бесконечно малая функция.
c) Произведение бесконечно малой на число есть функция бесконечно малая.