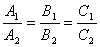Переход от одного вида уравнения прямой к другому.

Переход от общего уравнения прямой к другим видам уравнения прямой и обратно.

Существуют различные виды уравнения прямой на плоскости, описывающие одну и ту же линию. В зависимости от условий задачи удобно использовать тот или иной вид уравнения прямой. Поэтому, полезно уметь переходить от уравнения прямой одного вида к уравнению прямой другого вида. Цель этого пункта статьи заключается в приобретении навыков приведения общего уравнения прямой к другим видам уравнения прямой и обратно.

Начнем с приведения общего уравнения прямой к каноническому уравнению прямой вида .

Если , то переносим слагаемое в правую часть равенства с противоположным знаком 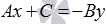. В левой части равенства выносим А за скобки . Полученное равенство можно записать как пропорцию вида .

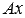Если , то оставляем в левой части общего уравнения прямой только слагаемое , а остальные переносим в правую часть с противоположным знаком: 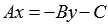. Теперь выносим в правой части равенства –B за скобки и записываем полученное равенство в виде пропорции . Вот и все.

Запоминать полученные формулы не имеет смысла, проще повторять указанные действия при приведении общего уравнения прямой к каноническому виду.

Плоскость в пространстве

Общее уравнение плоскости; его частные случаи.

Каждую плоскость в пространстве можно представить как линейное уравнение, называемое общим уравнением плоскости

, где .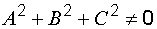

Коэффициенты 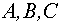являются координатами нормального вектора плоскости . Вектор перпендикулярен плоскости.

Частные случаи.

1. Если в уравнении (8) , то оно принимает вид Ax+By+Cz=0.Этому ур-ю удовлетворяет точка О(0;0;0). Следовательно, плоскость проходит через начало координат.

2. Если С=0, то имеем ур-е: Аx+By+D=0. Нормальный вектор n=(A,B,0) перпендикулярен оси Оz. Следовательно плоскость параллельна оси Оz, если В=0 – параллельна оси Оy, А=0 – параллельна оси Оx.

3. Если С=D=0, то плоскость проходит через О(0;0;0) параллельно оси Оz, т.е. плоскость Аx+By=0 проходит через ось Оz. Аналогично ур-ям Ву+Сz=0 и Ах+Сz=0 отвечают плоскости, порходящие соответственно через ос Ох и Оу.

4. Если А=В=0, то ур-е (8) принимает вид Сz+D=0, т.е. z= -D/C. Плоскость параллельна плоскости Оху. Аналогично ур-ям Ах+D=0 и Ву+D=0 отвечают плоскости, соответственно параллельные плоскостям Оух и Охz.

5. Если А=В=D=0, то ур-е (8) примет вид Сz=0, т.е. z=0. Это ур-е плоскости Оху. Аналогично у=0 – ур-е плоскости Охz, х=0 – ур-е плоскости Оуz.

Угол между двумя плоскостями; условия параллельности и перпендикулярности плоскостей

Угол между плоскостями. Угол φ между нормальными векторами n₁ и n₂ двух плоскостей является углом между плоскостями.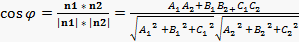

Условия перпендикулярности 2х плоскостей. Ясно, что две плоскости перпендикулярны тогда и только тогда, когда их нормальные векторы перпендикулярны, а следовательно, или .

Таким образом, .

3) Условия параллельности 2х плоскостей. Две плоскости α₁ и α₂ параллельны тогда и только тогда, когда их нормальные векторы 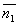и параллельны, а значит