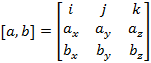Декартова прямоугольная система координат. Деление отрезка в данном отношении.

Декартова прямоугольная система координат

Определение 1. Осью называется прямая, на которой:

1) выбрана начальная точка ("начало" - точка О);

2) указано (стрелкой) положительное направление отсчета;

3) выбран масштаб.

Определение 2. Декартовой прямоугольной системой координат на плоскости (в пространстве) называют две (три) взаимно перпендикулярные оси с общим началом. Первая ось OX называется осью абсцисс, вторая ось OY - осью ординат (третья ось OZ - осью аппликат).

Каждой точке плоскости (пространства) ставится в соответствие упорядоченная пара (тройка) действительных чисел - координат данной точки.

Определение 3. Уравнением линии на плоскостиназывается уравнение с двумя переменными, такое, что только координаты любой точки, лежащей на этой линии, удовлетворяют данному уравнению.

Расстояние между двумя точками на плоскости

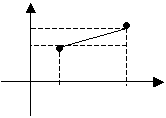
Даны две точки на плоскости с координатами A (x₁, y₁) и B (x₂, y₂).

Y

y₂ B

y₁ A C

0 x₁ x₂ X

Из треугольника ABC:

.

Деление отрезка в данном отношении

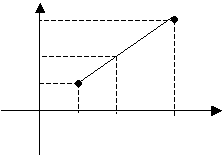
Пусть даны две точки M₁ (x₁, y₁) и M₂ (x₂, y₂). Найдем на отрезке M₁M₂ точку N, которая делила бы данный отрезок в отношении : .

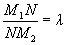Y

B₂ M₂

B N

B₁ M₁

0 A₁ A A₂ X

По теореме о пропорциональности отрезков прямых, пересеченных рядом параллельных прямых, получим

,

,

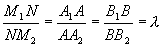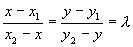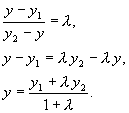
Координаты точки, делящей отрезок в данном отношении, находятся по этим формулам.

Если l = 1 , то деление отрезка производится пополам:

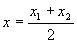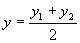, - формулы для нахождения координат середины отрезка.

Скалярное произведение векторов; скалярное произведение векторов, заданных координатами.

Скалярное произведение векторов.

Скалярным произведением вект. А и В называется число, равное произведению длин этих векторов, умноженному на косинус угла между ними

Свойства. 1) (a,b)=(b,a) (коммутативность). 2) (λa,b) =(a, λb) = λ (a,b) (ассоциативность). 3) дистрибутивно относительно сумсуммы (а+b,с)=(а,b)+(а,с) 4) Скалярное произведение двух векторов равно нулю тогда и только тогда когда хотя бы один из вект. нулевой либо они перпендикулярны (a • b = 0, если a ┴ b).

Скалярным квадратом называется скалярное произведение вектора на себя => равен квадрату длины вектора.

(a,b)= *|b|*Cos(a^b); пр_ab=(a,b)/ 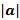(проекция a на b). Длина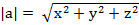

Скалярное произведение в коорд форме.Коорд орты i,j,k имеют длины, равные единицы i²=j²=k²=1, их взаимное произведение равно 0 . (a,b) =a_x*b_x+a_y*b_y+a_z*b_z. Cos и ПР находятся с помощью координат.

Векторное произведение векторов.
Векторным произведением вектора а на вектор b называется вектор с, который: 1) Перпендикулярен векторам a и b, т. е. с^а и с^b; 2) Имеет длину, численно равную площади параллелограмма, построенного на векторах а и b как на сторонах, т. е. 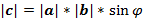. 3.Векторы a, b и с образуют правую тройку.

Свойства: 1. При перестановке сомножителей векторное произведение меняет знак, т.е. [а,b] =[b,a]; 2. Векторное произведение обладает сочетательным свойством относительно скалярного множителя, т. е. [а,b] = [а,b] = [b,a]; 3. Два ненулевых вектора а и b коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору, т. е. а||b <=>[а,b] =0. 4.распределительное свойство:[a+b,с]=[а,с]+[b,с].