Парабола — множетво всех точек плоскости, каждая из которых одинаково удалена от данной точк, называемой фокусом, и данной прямой, называемой директрисой. Расстояние от фокуса F до директрисы называется параметром параболы и обозначается через p (p >0). Кононическое уравнение параболы: y2=2px.
Пусть на плоскости заданы точка F и прямая 
, не проходящая через F. Парабола - множество всех тех точек M плоскости, каждая из которых равноудалена от точки F и прямой . Точка F называется фокусом, прямая - директрисой параболы; (OF) - ось, O - вершина,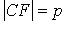 
- параметр, 
- фокус,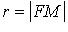 
- фокальный радиус.
Каноническое уравнение: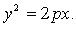 
Эксцентриситет: 
Фокальный радиус: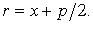 
Уравнение директрисы: 
Уравнение касательной в точке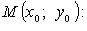 
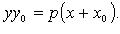
Свойство касательной к параболе: 
(М - точка касания; N - точка пересечения касательной с осью Ox).
Уравнение нормали в точке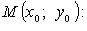 
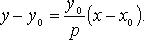
Уравнение диаметра, сопряженного хордам с угловым коэффициентом k: y = p/k.
Параметрические уравнения параболы: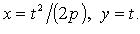 
Полярное уравнение: 
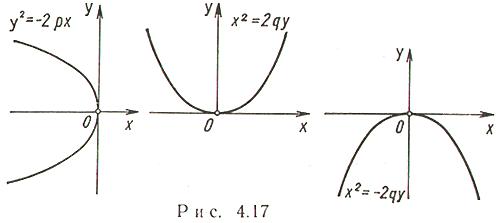
Другие формы канонического уравнения (рис. 4.17):
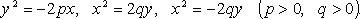
Полярная система координат 
Полярная система координат.
Полярная система координат – система плоских координат образованная направленным прямым лучом OX, называющимся полярной осью. Чаще всего за полярную ось принимают ось северного направления какого-либо меридиана. Начало координат - точка O - называется полюсом системы.
Положение любой точки в полярной системе определяется двумя координатами: радиусом-вектором r (или полярным расстоянием S) – расстоянием от полюса до точки, и полярным углом b при точке O, образованным осью OX и радиусом вектором точки и отсчитываемым от оси OX по ходу часовой стрелки.
Под полярным углом b в геодезии часто принимают дирекционный угол направления, с помощью которого определяют координаты точек и расстояния между ними.
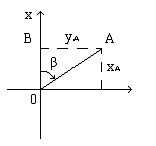Переход от прямоугольных координат к полярным и обратно для случая, когда начала обеих систем находятся в одной точке и оси OX у них совпадают, выполняется по формулам прямой геодезической задачи:
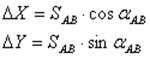
tgb=Y/X, b=arctg(Y/X)
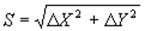
Эти формулы получаются из решения треугольника OBA по известным соотношениям между сторонами и углами прямоугольного треугольника. Системы прямоугольных и полярных координат применяются в геодезии для определения положения точек на плоскости.
Связь между полярными и декартовыми координатами одной и той же точки.
Поверхности второго порядка
Трехосный эллипсоид; каноническое уравнение; полуоси. Эллипсоид вращения.
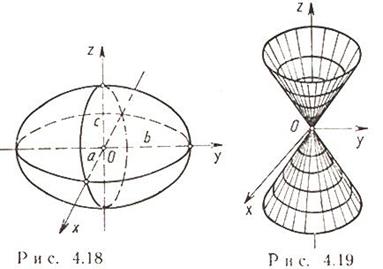
)эллипсоид x2/a2 + y2/b2 + z2/c2 = 1 a>0, b>0, c>0. симметричная поверхность отн. своих осей. Если a=b=c x2+y2+z2=a2 (сфера) a,b,c – полуоси эллипсоида.Точки(±a,0,0),(0,±b,0),(0,0,±c) – вершины эллипсоида.
Каноническое уравнение:
- трехосный эллипсоид;
- эллипсоид вращения вокруг оси Oz;
- эллипсоид вращения вокруг оси Oy;
- эллипсоид вращения вокруг оси Ox;
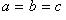- сфера.
Сечения эллипсоида плоскостями - либо эллипс (окружность), либо точка, либо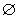 
.
