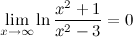Пусть F(x)=f(g(x)) - сложная функция.
Если предел g(x) при x стремящемся к x0 равен y0,
а предел f(у) при у стремящемся к у0 равен z0,
то тогда предел F(x) при x стремящемся к x0 равен z0.
Если функция у = f(x) имеет в точке а конечный предел b и не принимает значения b в некоторой о проколотой окрестности U(a) этой точки, а функция g(у) имеет в точке b конечный предел с, то сложная функция g(f(x)) имеет предел в точке а и он равен с.
73.Первый замечательный предел 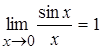 .
.
Теорема Первый замечательный предел равен 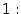

Доказательство. Рассмотрим два односторонних предела 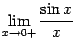 и
и 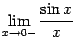 и докажем, что каждый из них равен 1. Тогда по теореме 2.1 двусторонний предел
и докажем, что каждый из них равен 1. Тогда по теореме 2.1 двусторонний предел 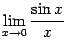 также будет равняться 1.
также будет равняться 1.
Итак, пусть 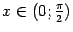 (этот интервал -- одно из окончаний базы
(этот интервал -- одно из окончаний базы  ). В тригонометрическом круге (радиуса
). В тригонометрическом круге (радиуса 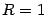 ) с центром
) с центром 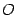 построим центральный угол, равный
построим центральный угол, равный 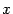 , и проведём вертикальную касательную в точке
, и проведём вертикальную касательную в точке 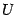 пересечения горизонтальной оси с окружностью (
пересечения горизонтальной оси с окружностью (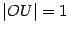 ). Обозначим точку пересечения луча с углом наклона
). Обозначим точку пересечения луча с углом наклона 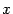 с окружностью буквой
с окружностью буквой  , а с вертикальной касательной -- буквой
, а с вертикальной касательной -- буквой 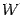 ; через
; через  обозначим проекцию точки
обозначим проекцию точки  на горизонтальную ось.
на горизонтальную ось.
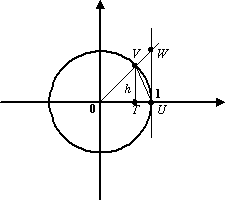
Рис.2.27.Тригонометрический круг
Пусть 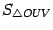 -- площадь треугольника
-- площадь треугольника  ,
, 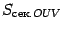 -- площадь кругового сектора
-- площадь кругового сектора  , а
, а 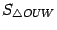 -- площадь треугольника
-- площадь треугольника 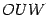 . Тогда очевидно следующее неравенство:
. Тогда очевидно следующее неравенство:
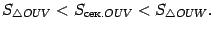
Заметим, что горизонтальная координата точки  равна
равна 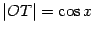 , а вертикальная --
, а вертикальная -- 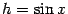 (это высота треугольника
(это высота треугольника  ), так что
), так что  . Площадь центрального сектора круга радиуса
. Площадь центрального сектора круга радиуса 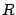 с центральным углом
с центральным углом 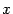 равна
равна 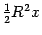 , так что
, так что 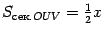 . Из треугольника
. Из треугольника 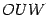 находим, что
находим, что 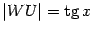 . Поэтому
. Поэтому 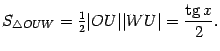 Неравенство, связывающее площади трёх фигур, можно теперь записать в виде
Неравенство, связывающее площади трёх фигур, можно теперь записать в виде
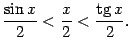
Все три части этого неравенства положительны, поэтому его можно записать так:
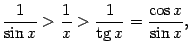
или (умножив на  ) так:
) так:
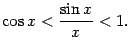
Предел постоянной 1 в правой части неравенства, очевидно, равен 1. Если мы покажем, что при  предел
предел 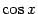 в левой части неравенства тоже равен 1, то по теореме "о двух милиционерах" предел средней части
в левой части неравенства тоже равен 1, то по теореме "о двух милиционерах" предел средней части 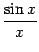 также будет равен 1.
также будет равен 1.
Итак, осталось доказать, что 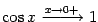 . Сперва заметим, что
. Сперва заметим, что 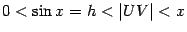 , так как
, так как 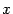 равняется длине дуги окружности
равняется длине дуги окружности 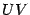 , которая, очевидно, длиннее хорды
, которая, очевидно, длиннее хорды  . Применяя теорему "о двух милиционерах" к неравенству
. Применяя теорему "о двух милиционерах" к неравенству

при  , получаем, что
, получаем, что
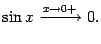
| (2.3) |
Простая замена переменной 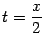 показывает, что и
показывает, что и 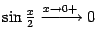 . Теперь заметим, что
. Теперь заметим, что  . Применяя теоремы о линейности предела и о пределе произведения, получаем:
. Применяя теоремы о линейности предела и о пределе произведения, получаем:
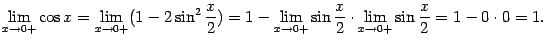
| (2.4) |
Тем самым показано, что

Сделаем теперь замену  ; при этом база
; при этом база  перейдёт в базу
перейдёт в базу 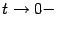 (что означает, что если
(что означает, что если 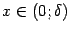 , то
, то 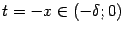 ). Значит,
). Значит,
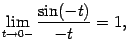
но  (
(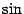 -- нечётная функция), и поэтому
-- нечётная функция), и поэтому
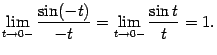
Мы показали, что левосторонний предел также равен 1, что и завершает доказательство теоремы.
Доказанная теорема означает, что график функции 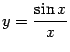 выглядит так:
выглядит так:

Рис.2.28.График 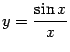
74.Второй замечательный предел 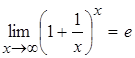 .
.
Второй замечательный предел существует. Его значение 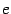 -- число, лежащее между
-- число, лежащее между  и
и 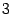 .
.
Более подробное изучение числа 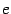 показывает, что
показывает, что 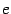 -- иррациональное число, несколько первых десятичных знаков которого таковы:
-- иррациональное число, несколько первых десятичных знаков которого таковы:
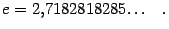
Для доказательства теоремы 2.15 нам понадобится следующая лемма; формула, в ней полученная, называется формулой бинома Ньютона.
Лемма 2.2 Пусть 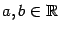 и
и 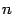 -- натуральное число. Тогда имеет место формула
-- натуральное число. Тогда имеет место формула
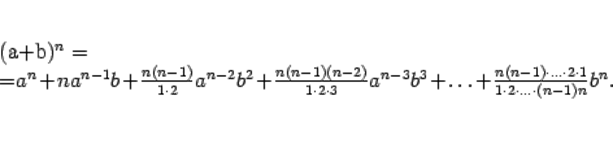
Заметим, что в дроби 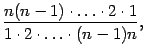 очевидно, сокращаются все сомножители в числителе и знаменателе, так что эта дробь равна 1. Аналогично, в предыдущем (не выписанном) слагаемом после сокращения получается коэффициент, равный
очевидно, сокращаются все сомножители в числителе и знаменателе, так что эта дробь равна 1. Аналогично, в предыдущем (не выписанном) слагаемом после сокращения получается коэффициент, равный 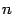 , в третьем справа слагаемом -- равный
, в третьем справа слагаемом -- равный 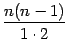 , и т. д. Таким образом, коэффициенты в слагаемых, стоящих на одинаковых местах, считая слева и справа от края формулы, совпадают.
, и т. д. Таким образом, коэффициенты в слагаемых, стоящих на одинаковых местах, считая слева и справа от края формулы, совпадают.
Доказательство. Доказывать утверждение леммы будем по индукции по параметру 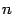 . При
. При 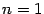 формула 2.2, очевидно, верна:
формула 2.2, очевидно, верна:
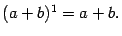
(Заметим, что при 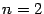 и
и  формула 2.2 также хорошо известна:
формула 2.2 также хорошо известна:
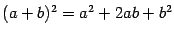
и

Предположим, что она верна для  , и докажем, что тогда она верна и при
, и докажем, что тогда она верна и при 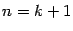 . Действительно,
. Действительно,
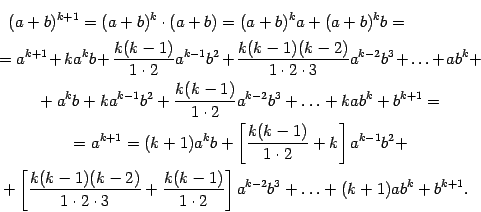
При этом в квадратных скобках получается:

| |
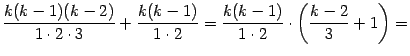
| |

|
и так далее, то есть как раз то, что должно получиться в качестве коэффициентов формулы бинома Ньютона при 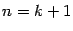 .
.
Д оказательство теоремы 2.15. Рассмотрим последовательность 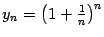 и применим к
и применим к 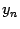 формулу бинома Ньютона при
формулу бинома Ньютона при  и
и 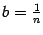 . Получим
. Получим
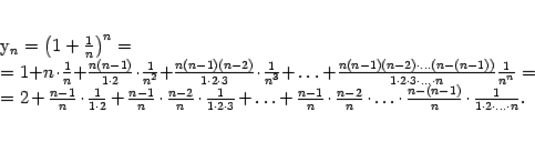
Покажем, что последовательность 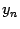 ограничена сверху. Для этого заменим все дроби
ограничена сверху. Для этого заменим все дроби 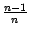 ,
, 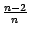 ,...,
,..., 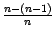 на 1. Все эти дроби меньше 1, так что сумма в правой части формулы (Доказательство теоремы 2.15) увеличится:
на 1. Все эти дроби меньше 1, так что сумма в правой части формулы (Доказательство теоремы 2.15) увеличится:

Далее, заменим все числа  в знаменателях этих слагаемых на 2; от этого правая часть ещё увеличится. Получим:
в знаменателях этих слагаемых на 2; от этого правая часть ещё увеличится. Получим:

В правой части получилась сумма членов геометрической прогрессии. Она равна
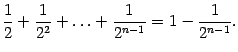
Поэтому
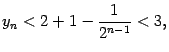
что и означает ограниченность последовательности сверху числом 3.
Покажем теперь, что последовательность 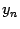 не убывает. Действительно, запишем формулу (Доказательство теоремы 2.15) в виде
не убывает. Действительно, запишем формулу (Доказательство теоремы 2.15) в виде
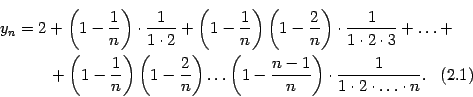
В аналогичной формуле, написанной для  вместо
вместо 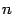 , во-первых, увеличится каждое из выражений в круглых скобках (так как вычитаемое уменьшится) и, значит, увеличатся все слагаемые, содержащие такие скобки. Во-вторых, число слагаемых увеличится на одно: добавится положительное слагаемое
, во-первых, увеличится каждое из выражений в круглых скобках (так как вычитаемое уменьшится) и, значит, увеличатся все слагаемые, содержащие такие скобки. Во-вторых, число слагаемых увеличится на одно: добавится положительное слагаемое
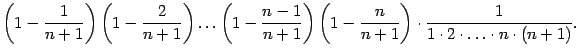
Следовательно, при росте номера 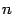 члены последовательности
члены последовательности 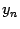 строго возрастают:
строго возрастают:  при всех
при всех  .
.
Применим теперь к возрастающей ограниченной сверху последовательности 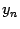 теорему о пределе монотонной ограниченной функции (теорема 2.13) и получим, что существует предел
теорему о пределе монотонной ограниченной функции (теорема 2.13) и получим, что существует предел
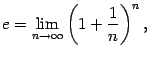
причём число 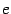 не больше постоянной 3, ограничивающей последовательность. Осталось заметить, что
не больше постоянной 3, ограничивающей последовательность. Осталось заметить, что  . Так как все последующие члены
. Так как все последующие члены 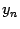 ещё больше, то и предел
ещё больше, то и предел 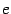 , на основании теоремы о переходе к пределу в неравенстве (следствие 2.7), не меньше числа
, на основании теоремы о переходе к пределу в неравенстве (следствие 2.7), не меньше числа  , что и завершает доказательство теоремы.
, что и завершает доказательство теоремы.
Замечание 2.7 Можно также показать, что

| (2.5) |
однако строгое доказательство достаточно тяжело, и мы его здесь пропускаем.
В формуле (2.5) можно сделать замену  , при этом база
, при этом база  перейдёт в базу
перейдёт в базу 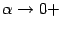 , и мы получим
, и мы получим

Непрерывность и односторонняя непрерывность функции в точке. Основные понятия и определения.
Функция 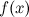 называется непрерывной в точке
называется непрерывной в точке  , если:
, если:
1. функция 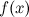 определена в точке
определена в точке  и ее окрестности;
и ее окрестности;
2. существует конечный предел функции 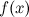 в точке
в точке  ;
;
3. это предел равен значению функции в точке  , т.е.
, т.е. 
Замечание. При нахождении предела функции 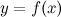 , которая является непрерывной, можно переходить к пределу под знаком функции, то есть
, которая является непрерывной, можно переходить к пределу под знаком функции, то есть
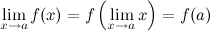
Пример. Задание. Вычислить предел 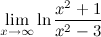
Решение. 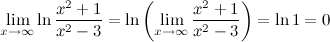
Ответ.