Дифференциал функции в точке x и обозначают  или
или 
Следовательно,
 (1)
(1)
или
 , (2)
, (2)
поскольку дифференциал функции y = f (x) равен произведению её производной на приращение независимой переменной.
Замечание. Нужно помнить, что если x – исходное значение аргумента, а  - наращенное значение, то производная в выражении дифференциала берётся в исходной точке x; в формуле (1) этого не видно из записи.
- наращенное значение, то производная в выражении дифференциала берётся в исходной точке x; в формуле (1) этого не видно из записи.
Дифференциал функции можно записать в другой форме:
 (3)
(3)
или
 (4)
(4)
Пусть, например, требуется вычислить приближенное значение функции

в точке  . Значение
. Значение  в близкой к
в близкой к  точке
точке  находится легко:
находится легко:  . График
. График  в окрестности точки
в окрестности точки  близок к прямой
близок к прямой  — касательной к нему в точке с абсциссой
— касательной к нему в точке с абсциссой  . Поэтому
. Поэтому  . Имеем
. Имеем 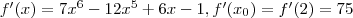 и
и  .Вычисления на калькуляторе дают результат
.Вычисления на калькуляторе дают результат  .Вообще для дифференцируемой в точке
.Вообще для дифференцируемой в точке  функции
функции  при
при  , мало отличающихся от нуля, ее график близок к касательной (проведенной в точке графика с абсциссой
, мало отличающихся от нуля, ее график близок к касательной (проведенной в точке графика с абсциссой  ), т. е. при малых
), т. е. при малых 
 (1)
(1)
Если точка  такова, что значения
такова, что значения  и
и  нетрудно вычислить, то формула (1) позволяет находить приблиенный значения
нетрудно вычислить, то формула (1) позволяет находить приблиенный значения  при
при  , достаточно близком к
, достаточно близком к  . Так, при вычислении значения
. Так, при вычислении значения  естественно взять в качестве
естественно взять в качестве  число
число  , так как
, так как  близко к
близко к  и значения
и значения  и
и  при
при  найти нетрудно:
найти нетрудно:  . По формуле (1) получаем
. По формуле (1) получаем  полчаем:
полчаем:

Формулой (1) часто пользуются для вычисления приближеных значений и других функций, например тригонометрических. Так, для вычисления  удобно взять
удобно взять  , при этом
, при этом 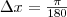 (так как
(так как  ). Имеем
). Имеем  и
и

т.е.  . Вычисляя значения
. Вычисляя значения  на калькуляторе, получаем
на калькуляторе, получаем  .
.
Теорема о дифференцировании суммы (разности) дифференцируемых функций.
Для доказательства второго правила дифференцирования 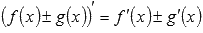 воспользуемся определением производной и свойством предела непрерывной функции.
воспользуемся определением производной и свойством предела непрерывной функции.

Подобным образом можно доказать, что производная суммы (разности) n функций равна сумме (разности) n производных 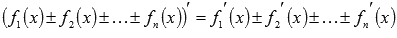 .
.
Производная алгебраической суммы функций
выражается следующей теоремой.
Теорема 1. Производная суммы (разности) двух дифференцируемых функций равна сумме (разности) производных этих функций:
(u±v)' = u'±v'
Следствие. Производная конечной алгебраической суммы дифференцируемых функций равна такой же алгебраической сумме производных слагаемых. Например,
(u — v + w)' = u' — v' + w'
Теорема о дифференцировании произведения (частного) дифференцируемых функций.
Производную произведения функций определяет
Теорема 2. Производная произведения двух дифференцируемых функций равна произведению первой функции на производную второй плюс произведение второй функции на производную первой, т. е.
(uv)' = u'v + uv'
Следствие 1. Постоянный множитель можно выносить за знак производной (cv)' = cv' (с = const).
Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждой из них на все остальные.
Например, (uvw)' = u'vw + uv'w + uvw'
Производная частного двух функций
выражается следующей теоремой.
Теорема 3. Производная частного двух дифференцируемых функций определяется формулой

88.Теорема о дифференцировании обратной функции.