Сравнение бесконечно малых функций. Эквивалентные функции.

Пусть a (x) и b (x) – б.м. функции при x ® a (x ® + ¥, x ® –¥, x ® x ₀,...). Рассмотрим предел их отношения при x ® a.

1. Если = b и b – конечное число, b ¹ 0, то функции a (x), b (x) называются бесконечно малыми одного порядка малости при x ® a.

2. Если = 0, то a (x) называют бесконечно малой высшего порядка, чем b (x) при x ® a. Очевидно, в этом случае = ¥.

3. Если a (x) – б.м. высшего порядка, чем b (x), и = b ¹ 0 (b – конечное число, k Î N), то a (x) называют бесконечно малой k -го порядка, по сравнению с b (x) при x ® a.

4. Если не существует (ни конечный, ни бесконечный), то a (x), b (x) называют несравнимыми б.м. при x ® a.

5. Если = 1, то a (x), b (x) называются эквивалентными б.м. при x ® a, что обозначается так: a (x) ~ b (x) при x ® a.

Теорема 1. Пусть a (x) ~ a ₁(x), b (x) ~ b ₁(x) при x ® a. Если существует , то существует и , и = .

Доказательство. = 1, = 1,

6. = = .

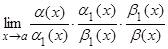Эта теорема позволяет упрощать нахождение пределов.

Теорема 2. Бесконечно малые функции a (x) и b (x) эквивалентны (при x ® a) тогда и только тогда, когда a (x) – b (x) является б.м. высшего порядка, по сравнению с a (x) и b (x) (при x ® a).

Доказательство

Пусть a (x) ~ b (x) при x ® a. Тогда = = 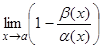0, т.е. разность a (x) – b (x) – б.м. высшего порядка, по сравнению с a (x) при при x ® a (аналогично с b (x)).

Пусть a (x) – b (x) – б.м. высшего порядка, по сравнению с a (x) и b (x), покажем, что a (x) ~ b (x) при x ® a:

= = + = 1,

т.е. a (x) ~ b (x) при x ® a.

Теорема 3. Сумма конечного числа бесконечно малых различных порядков эквивалентна слагаемому низшего порядка.

Доказательство. Пусть a (x) – б.м. низшего порядка по сравнению с b (x) и g (x) при x ® a, т.е. = 0 и = 0.

Покажем, что a (x) ~ (a (x) + b (x) + g (x)) при x ® a:

= + + = 1 + 0 + 0 = 1.

Доказанные теоремы применяются для нахождения пределов.

Дифференциальное исчисление функций одной переменной

Производная и односторонние производные функции в точке. Основные понятия и определения.

Определение. Правой (левой) производной функции f(x) в точке х = х₀ называется правое (левое) значение предела отношения при условии, что это отношение существует.

Если функция f(x) имеет производную в некоторой точке х = х₀, то она имеет в этой точке односторонние производные. Однако, обратное утверждение неверно. Во- первых функция может иметь разрыв в точке х₀, а во- вторых, даже если функция непрерывна в точке х₀, она может быть в ней не дифференцируема. Пусть x, y – переменные величины. Если каждому значению переменных x из множества A соответствует по определенному закону единственное значение переменной y, то говорят, что y является функцией (однозначной) от x и пишут y = f(x) или y = y(x). При этом переменную x называют аргументом или независимой переменной, множество A – областью определения функции y = f(x). Обозначим множество всех значений функции, т.е. {f(x)|x Î A}, через B.

Например: f(x) = ïxï- имеет в точке х = 0 и левую и правую производную, непрерывна в этой точке, однако, не имеет в ней производной.

Теорема. (Необходимое условие существования производной) Если функция f(x)имеет производную в точке х₀, то она непрерывна в этой точке.

Понятно, что это условие не является достаточным.

Определение производной

Односторонние производные

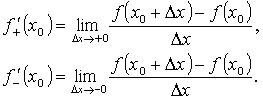
Геометрический и механический смысл производной функции в точке.

Определение

Средней скоростью изменения функции при переходе независимой переменной от значения к значению называется отношение приращения функции к приращению независимой переменной, то есть

Определение

Истинной или мгновенной скоростью изменения функции при заданном значении независимой переменной называется предел, к которому стремится средняя скорость изменения функции при стремлению к нулю приращения аргумента :