Под неявним заданием функции понимают задание функции в виде уравнения F(x; у) = 0, не разрешенного относительно у.Всякую явно заданную функцию у = f (х) можно записать как
неявно заданную уравнением f(x) - у = 0, но не наоборот.Не всегда легко, а иногда и невозможно разрешить уравнение относительноу. Если неявная функция задана уравнением F(x; у) = 0, то для нахождения производной от y по х нет необходимости разрешать уравнение
относительно у: достаточно продифференцировать этоуравнение по х, рассматривая при этом у как функцию х,и полученное затем уравнение разрешить относительно у'.Производная неявной функции выражается через аргумент х ифункцию у.Найдем производную y’x, считая, что функции x=x(t) и y=y(t) имеют производныеи что функция х = x(t) имеет обратную t = φ(x). По правилу дифференцирования обратной функции: 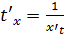
94.Инвариантность формы дифференциала первого порядка.
Инвариантность формы дифференциала первого порядка Найти производную показательно-степенной функции y=. Справочный материал и примеры к выполнению контрольной работы по математике
Пусть задана сложная функция y=F(t)=f(g(t)), y=f(x), x=g(t).
dy=(f(g(t))¢ dt=f¢(x)g¢(t)dt=f¢(x)dg=f¢(x)dx. Вид первого дифференциала такой же, как и в случае, когда x является независимой переменной. Это свойство называется свойством инвариантности дифференциала первого порядка.
Для дифференциалов высших порядков свойства инвариантности, вообще говоря, нет.
dy=f¢dx, d 2y=f¢¢dx2+f¢d 2x, для функции x=t2, второй дифференциал d 2x ¹ 0. Формула Тейлора. Степенные ряды
Замечание. (Важный частный случай, когда свойство инвариантности наблюдается и для старших дифференциалов). В случае, когда внутренняя функция суперпозиции линейна, свойство инвариантности сохраняется для дифференциалов произвольных порядков.
d ny, y=f(x), x=at+b, dx = a dt, d 2x=…=d nx=0. Таким образом, n-ый дифференциал
· Математика решение задач Направление вектора определяется углами, образованными им с осями координат Векторная алгебра
d nf=f(n)dxn имеет такой же вид, как и в случае независимого переменного x.
Кривые второго порядка.
Кривая второго порядка может быть задана уравнением
Ах2 + 2Вху + Су2 + 2Dx + 2Ey + F = 0.
Существует система координат (не обязательно декартова прямоугольная), в которой данное уравнение может быть представлено в одном из видов, приведенных ниже.
- уравнение эллипса.
- уравнение “мнимого” эллипса.
- уравнение гиперболы.
a2x2 – c2y2 = 0 – уравнение двух пересекающихся прямых.
y2 = 2px – уравнение параболы.
y2 – a2 = 0 – уравнение двух параллельных прямых.
y2 + a2 = 0 – уравнение двух “мнимых” параллельных прямых.
y2 = 0 – пара совпадающих прямых.
(x – a)2 + (y – b)2 = R2 – уравнение окружности.
Дифференциалы функции высших порядков.
Пусть у = f(х) дифференцируемая функция, а ее аргумент х –независимая переменная. Тогда ее первый дифференциал dy = f’(х) dxесть также функция х; можно найти дифференциал этой функции.Дифференциал от дифференциала функции у = f(x) называетсяее вторым дифференциалом (или дифференциалом второго порядка) иобозначается d2y или d2f(x). 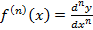 т.е. производную функции можно рассматривать как отношение еедифференциала соответствующего порядка к соответствующей степенидифференциала независимой переменной.(только если x–независимая переменная)
т.е. производную функции можно рассматривать как отношение еедифференциала соответствующего порядка к соответствующей степенидифференциала независимой переменной.(только если x–независимая переменная)
Теорема Ферма.
Теорема Ролля.
Теорема Лагранжа.
Теорема Коши.
Дифференциал суммы, произведения и частного двухдифференцируемых функций определяются следующими формулами:d(u+v)=du+dv, d(uv)=v*du+u*dv, d(u/v)=(v*du-u*dv)/v2. Дифференциал сложной функции равен произведению производной этой функции по промежуточному аргументу надифференциал этого промежуточного аргумента.
Теорема Ферма. Если функция у = f (х), определенная в интервале (а;b), достигает в некоторой точке с этого интервала наибольшего (или наименьшего) значения и существует производная f ′(с), то f ′(с) = 0. Теорема Ролля. Если функция у = f (х), непрерывная на отрезке [а; b] и дифференцируемая в интервале (а; b), принимает на концах этого отрезка равные значения f (a) = f (b), то в интервале (а; b) существует такая точка с, что f ′(с) = 0.
Теорема Лагранжа. Если функция у = f (х) непрерывна на отрезке [а; b] и дифференцируема в интервале (а; b), то в этом интервале найдется такая точка с, что 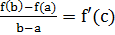 . Следствие. Если f ′(x) = 0 в интервале (а; b), то в этом интервале функция f (х) постоянна.
. Следствие. Если f ′(x) = 0 в интервале (а; b), то в этом интервале функция f (х) постоянна.
Теорема Коши. Если функции f (х) и g (х): 1) непрерывны на отрезке [а; b]; 2) дифференцируемы в интервале (а; b); 3) g'(x) ≠ 0 в этом интервале, то в интервале (а; b) существует такая точка с, что имеет место равенство 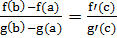
Правило Лопиталя.
(Правило Лопиталя раскрытия неопределенностей 0/0) Пусть функции f(x) и φ(х) непрерывны и дифференцируемыв окрестности точки х0 и обращаются в нуль в этой точке: f(x0) = φ(х0) = 0. Пусть φ(х) ≠0 в окрестности точки х0. (Правило Лопиталя раскрытия неопределенностей вида  ) Если существует предел
) Если существует предел 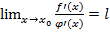 , то
, то 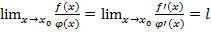 . Пусть функции f(x) и
. Пусть функции f(x) и 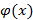 непрерывны и дифференцируемы в окрестности точки х0 (кроме, может быть, точки х0), в этой окрестности
непрерывны и дифференцируемы в окрестности точки х0 (кроме, может быть, точки х0), в этой окрестности 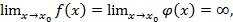
 Если существует предел
Если существует предел 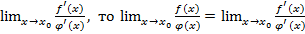 . Раскрытие неопределенностей различных видов. Правило Лопиталя применяется для раскрытия неопределенностей вида 0/0 и ∞/∞ которые называют основными. Неопределенности
. Раскрытие неопределенностей различных видов. Правило Лопиталя применяется для раскрытия неопределенностей вида 0/0 и ∞/∞ которые называют основными. Неопределенности
вида 0*∞, ∞-∞, 1∞, ∞0, 00 сводятся к двум основным видам путем тождественных преобразований.
Формула Тейлора. Многочлен Тейлора. Основные понятия и определения.