Функция y=f(x) называется возрастающей на интервале (a;b), если для любых x1 и x2 из этого интервала таких, что x1<x2, справедливо f(x1)<f(x2). Например, функции y=ax, y=logax при a>1, y=arctg x, y=arcsin x, 
(nÎN) возрастают на всей своей области определения.
График возрастающей функции
· Функция y = f(x) называется убывающей на интервале (a;b), если для любых x1 и x2 из этого интервала таких, что x1<x2, справедливо f(x1)>f(x2). Например, функции y=ax, y=logax при 0< a<1, y=arcctg x, y=arccos x убывают на всей своей области определения.
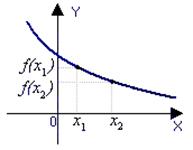
График убывающей функции
· Убывающие и возрастающие функции вместе образуют класс монотонных функций. Монотонные функции обладают рядом специальных свойств.
функция f(х), монотонная на отрезке [ а,b ], ограничена на этом отрезке;
· сумма возрастающих (убывающих) функций является возрастающей (убывающей) функцией;
· если функция f возрастает (убывает) и n – нечетное число, то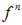 
также возрастает (убывает);
· если f'(x)>0 для всех xÎ(a,b), то функция y=f(x) является возрастающей на интервале (a,b);
· если f'(x)<0 для всех xÎ(a,b), то функция y=f(x) является убывающей на интервале (a,b);
· если f(x) – непрерывная и монотонная функция на множестве Х, то уравнение f(x)=C, где С – данная константа, может иметь на Х не более одного решения;
· если на области определения уравнения f(x)=g(x) функция f(x) возрастает, а функция g(x) убывает, то уравнение не может иметь более одного решения.
Теорема. (достаточное условие монотонности функции). Если непрерывная на отрезке [ а, b ] функция у = f (х) в каждой точке интервала (а, b) имеет положительную (отрицательную) производную, то эта функция возрастает (убывает) на отрезке [ а, b ].
Доказательство. Пусть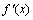 
>0 для всех хÎ (а,b). Рассмотрим два произвольных значения x2 > x1, принадлежащих [ а, b ]. По формуле Лагранжа 
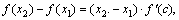х1<с < х2. 
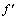(с) > 0 и х2 – х1 > 0, поэтому 
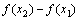> 0, откуда 
> 
, то есть функция f(х) возрастает на отрезке [ а, b ]. Аналогично доказывается вторая часть теоремы.
|
|
Теорема 3. (необходимый признак существования экстремума функции). Если дифференцируемая в точке c функция у = f (х) имеет в этой точке экстремум, то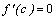 
.
Доказательство. Пусть, например, функция у = f (х) имеет в точке c максимум. Это означает, что существует такая проколотая окрестность точки c, что для всех точек x этой окрестности выполняется f (x) < f (c), то есть f (c) – наибольшее значение функции в этой окрестности. Тогда по теореме Ферма .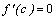
Аналогично доказывается случай минимума в точке c.
Замечание. Функция может иметь экстремум в точке, в которой ее производная не существует. Например, функция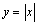 
имеет минимум в точке x = 0, хотя 
не существует. Точки, в которых производная функции равна нулю или не существует, называются критическими точками функции. Однако не во всех критических точках функция имеет экстремум. Например, функция у = x3 не имеет экстремумов, хотя ее производная 
=0.
Теорема 4. (достаточный признак существования экстремума). Если непрерывная функция у = f (x) имеет производную 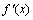во всех точках некоторого интервала, содержащего критическую точку С (за исключением, может быть, самой этой точки), и если производная 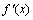при переходе аргумента слева направо через критическую точку С меняет знак с плюса на минус, то функция в точке С имеет максимум, а при перемене знака с минуса на плюс – минимум.
|
|
Доказательство. Пусть c – критическая точка и пусть, например, при переходе аргумента через точку c 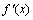меняет знак с плюса на минус. Это означает, что на некотором интервале (c–e; c) функция возрастает, а на интервале (c; c+e) – убывает (при e >0). Следовательно, в точке 
с функция имеет максимум. Аналогично доказывается случай минимума.
Замечание. Если производная 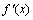не меняет знака при переходе аргумента через критическую точку, то функция в этой точке не имеет экстремума.
Так как определения предела и непрерывности для функции нескольких переменных практически совпадает с соответствующими определениями для функции одной переменной, то для функций нескольких переменных сохраняются все свойства пределов и непрерывных функций