Точки разрыва функции и их классификация.

Рассмотрим некоторую функцию f(x), непрерывную в окрестности точки х₀, за исключением может быть самой этой точки. Из определения точки разрыва функции следует, что х = х₀является точкой разрыва, если функция не определена в этой точке, или не является в ней непрерывной.

Следует отметить также, что непрерывность функции может быть односторонней. Поясним это следующим образом.

Если односторонний предел (см. выше) , то функция называется непрерывной справа.

х₀

Если односторонний предел (см. выше) , то функция называется непрерывной слева.

х₀

Определение. Точка х₀ называется точкой разрыва функции f(x), если f(x) не определена в точке х₀ или не является непрерывной в этой точке.

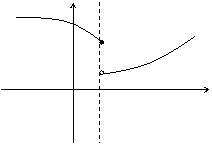
Определение. Точка х₀ называется точкой разрыва 1- го рода, если в этой точке функция f(x) имеет конечные, но не равные друг другу левый и правый пределы.

Для выполнения условий этого определения не требуется, чтобы функция была определена в точке х = х₀, достаточно того, что она определена слева и справа от нее.

Из определения можно сделать вывод, что в точке разрыва 1 – го рода функция может иметь только конечный скачок. В некоторых частных случаях точку разрыва 1 – го рода еще иногда называют устранимой точкой разрыва, но подробнее об этом поговорим ниже.

Определение. Точка х₀ называется точкой разрыва 2 – го рода, если в этой точке функция f(x) не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен.

77. Непрерывность основных элементарных функций.

Непрерывность элементарных функций.

Цель этого раздела - доказать факт, которым мы уже пользовались: любая элементарная функция непрерывна в любой точке своей области определения.

5.3.1. Непрерывность рациональных функций: 1. Постоянная функция y(х) = C = const, очевидно, непрерывна в любой точке (предел постоянной функции равен этой постоянной в любой точке).

Функция y(х)= х непрерывна в любой точке х (для "e>0 возьмём d = e, тогда если | х- х0|<d, то | f(х)- f(х0)| = | х- х0|<e=d).

Функция y(х)= х2 = х х непрерывна в любой точке х как произведение двух непрерывных функций.

По индукции функция y(х)= хn = хn-1 х непрерывна в любой точке х как произведение двух непрерывных функций. По той же причине непрерывна функция y(х)= аnхn, где аn=C=const.

Рациональная функция непрерывна в любой точке х как сумма непрерывных функций.

5.3.2. Непрерывность дробно-рациональных функций: непрерывна в любой точке х, в которой знаменатель отличен от 0, как частное непрерывных функций.

Непрерывность показательной функции . Требуется доказать, что . Рассмотрим разность (формула 6 табл.4.4.10) . Эта разность - БМ функция при х® х0, следовательно, ах® при при х® х0.

Непрерывность логарифмической функции . По формуле 7 табл.4.4.10 эквивалентных БМ ~

5.3.5. Непрерывность тригонометрических функций: а. .

при х ® х0 (мы воспользовались неравенством |sin х |£| х|, доказанным в 4.4.7.1. Первый замечательный предел).

б. непрерывна как суперпозиция непрерывных функций.

в. Функции и непрерывны в точках, в которых они определены, как частное непрерывных функций.

5.3.6. Гиперболические функции непрерывны (thx в точках, в которых shx¹0), так как они определяются через непрерывную функцию ех. Обратные гиперболические функции непрерывны, так как они выражаются через непрерывную функцию ln x.

Мы доказали непрерывность основных элементарных функций (кроме обратных тригонометрических, о которых ниже). Отсюда следует непрерывность всех элементарных функций в любой точке их областей определения, так как они определяются как функции, получающиеся из основных элементарных с помощью конечного числа арифметических действий и суперпозиций.

5.3.7. Из доказанного следует непрерывность показательно-степенной функции , , так как она представляется в виде 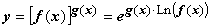, т.е. в виде суперпозиции непрерывных показательной и логарифмической функций.