События можно разделить на: достоверные, случайные и невозможные.
Случайным событием называется такое событие, которое при выполнении комплекса условий может произойти, а может и нет. Будем его обозначать буквами А, В, С и т.д.
Примеры. Выпадение "герба" при бросании монеты; появление на выходе приемника помехи в некотором интервале времени его работы; подавление радиоимпульса помехой.
Полной группой событий называются несколько событий таких что в результате опыта непременно должно произойти хотя бы одно из них.
События называют несовместными, если появление одного из них исключает появления других событий в одном и том же испытании.
События называют равновозможными, если есть основания считать, что ни одно из них не является более возможным, чем другое.
Множество всех элементарных событий, имеющих место в результате случайного эксперимента, будем называть пространством элементарных событий W (элементарное событие соответствует элементарному исходу).
Случайными событиями (событиями), будем называть подмножества пространства элементарных событий W.
Пример 1. Подбросим монету один раз. Монета может упасть цифрой вверх - элементарное событие w1, или гербом - элементарное событие w2. Соответствующее пространство элементарных событий W состоит из двух элементарных событий:
W = {w 1,w 2}.
Привести классификацию случайных явлений. Дать определение случайной величины и проанализировать связь с пространством случайных событий.
Смотри ответ на вопрос №18
Определить вероятность случайного события. Сформулировать основные аксиомы и законы теории вероятностей.
Вероятность – числовая характеристика степени возможности появления какого-либо случайного события при тех или иных определенных, могущих повторяться неограниченное число раз условиях
|
|
Способы задания вероятности: Аксиоматический, классический, статистическая вероятность, геометрический
Вероятностью события А называют сумму вероятностей элементарных событий, составляющих событие А:
.
Из определения вероятности события P(A) вытекают следующие свойства вероятности:
0£P(A); - аксиома неотрицательности;
P(W)=1; - аксиома нормировки;
Аксиома адитивности (сложения):
Если А иВ несовместные события (А Ì W, В Ì W,А·В= Æ), то Р(А+В)=Р(А)+Р(В).
Аксиома аддитивности может быть расширена на случай n попарно несовместимых событий, т.е.
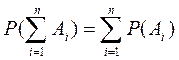, A i ÎW; Ai·A j =Æ; i,j = 
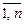, i¹j.
Вероятность суммы несовместимых событий равна сумме вероятностей этих событий.
Аксиому сложения вероятностей иногда называют теоремой сложения вероятностей, или правилом сложения вероятностей.
Если имеется счетное множество несовместимых событий А1,А2…Аn… (Ai·A j =Æ; i¹j) то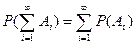 
;
Следствия из аксиом теории вероятностей:
Следствие 1: Если А Ì В, (влечении В), то Р(А)<Р(В).
Следствие 2: Р(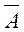
)=1-Р(А); А+ 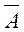=W; по аксиоме 3, А· 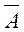=Æ,
Р(А)+Р(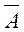)=Р(А+ 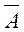)=Р(W)=1;
Следствие 3: Р(Æ)=0;
Следствие 4: Если А и В совмесимые события, наблюдаемые в одном и том же пространстве элементарных событий, W, тогда Р(А+В)=Р(А)+Р(В)-Р(А·В).