Определить функцию распределения системы двух с. в и ее основные свойства. Привести геометрическую интерпретацию, указать практическое применение.

Центральная предельная теорема теории вероятностей и ее практическое использование в задачах синтеза ТКС.

Теорема. Если случайные величины Х₁, Х₂,..., Х_n взаимно независимы и имеют один и тот же закон распределения f(x) и

то при неограниченном увеличении n закон распределения суммы неограниченно приближается к нормальному.

Она может быть сформулирована в более общем случае. Закон распределения вероятностей суммы независимых случайных величин одинакового порядка при неограниченном увеличении слагаемых вне зависимости законов распределения слагаемых стремится к нормальному закону с плотностью вероятностей

где

Теорема Чебышева и ее практическое использование в задачах анализа ТКС.

Пусть m_x и D_x – математическое ожидание и дисперсия случайной величины Х. Тогда неравенство Чебышева гласит: вероятность того, что отклонение случайной величины от ее математического ожидания будет по абсолютной величине не меньше любого положительного числа , ограничена величиной , т.е.

Теорема: при неограниченном увеличении числа независимых испытаний, среднее арифметическое значение дисперсии, сходится по вероятности от ее математического ожидания.

Определить понятие системы случайных величин. Дать определение зависимых случайных величии. Привести критерии независимости двух с. в., используемые практически.

Система случайных величин - упорядоченный набор (x1,x2,…xn) слу.величин Xi(i=1,n), заданных на одном и том же Пространстве Элементарных Событий Ω (называется n-мерной случайной величиной)

Две слу.величины называются зависимыми, если закон распределения вероятностей одной из них меняется в зависимости от того, какое значение принимает другая.

Если слу.вел. независимы, то

f(x,y)=f(x)*f(y)

K_xy=0(корреляционный момент=0, отсутствует линейная зависимость)

M[x y] =m_x* m_y (математическое ожидание)

r_xy=K_xy/(σ_x*σ_y); 0<=|r_xy|<=1

коефициент корреляции

Определить основные свойства с.в, имеющей равномерное распределение.

Непрерывная случайная величина X имеет равномерное распределение на интервале [x₁, x₂], если на этом интервале плотность вероятности постоянна, а вне его равна нулю:

Числовые характеристики:

M(x)=(x₁+x₂)/2

D(x)=((x₂- x₁)^2)/2

Функция распределения

Обосновать использование такой с.в. для получения белого шума.

Белый шум - случайный процесс с нулевым мат.ожиданием, имеющий автокорреляционную функцию, являющейся дельта-функцией Дираса.

M(t)=0

K(t₁,t₂)=σ²*ϑ*(t₁-t₂)

Определить функцию распределения системы двух с. в и ее основные свойства. Привести геометрическую интерпретацию, указать практическое применение.

Функцией распределения вероятностей F(x) или интегральным законом распределения случайной величины Х называется вероятность того, что случайная величина Х примет значение меньше х:

Двумерная функция распределения вероятностей случайных величин X и Y – это вероятность события [X<x,Y<y]

, где (X<x,Y<y) геометрическая интерпретация- случайная точка на плоскости XOY

Из определения функции распределения вероятностей следуют следующие ее свойства:

1) ;

2) ;

3)

4) не убываемая функция по одной переменной;

5) - функция распределения слу.вел. X и Y

6) Вероятность попадания (X,Y) в пределы прямоугольника R

8. Определить функцию плотности распределения вероятности системы двух с. в. и ее основные свойства. Привести геометрическую интерпретацию, указать практическое применение.

Плотностью распределения случайных величин (X,Y) определяется соотношением:

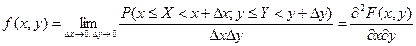, если предел существует.

Свойства плотности распределения:

1) ;

2) ;

3)

4) , где f_x(x) и f_y(y) – плотности распределения слу.вел. X и Y

5)

Геометрически - некая поверхность