Способы:
Множество может быть задано следующими способами: списком его элементов, порождающей процедурой и описанием свойств его элементов.
I. Списком могут быть заданы только конечные множества.  ;
;
этот способ не пригоден для задания бесконечных множеств и даже в случае конечных множеств не всегда практически реализуем.
II. Порождающая процедура описывает способ получения элементов множества из уже полученных элементов; используется для задания бесконечных и конечных множеств. Например, множество  порождающая процедура для которого определяется следующими двумя правилами:
порождающая процедура для которого определяется следующими двумя правилами:
1) 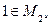 ;
;
2) если  то
то  .
.
Правила, описанные таким образом называются индуктивными или рекурсивными.
III. Задание множества описанием свойств его элементов. В случае, когда свойство элементов множества М может быть описано коротким выражением ρ(х), множество М задания при помощи обозначается:
М={х  ρ(х)}, которое читается так: М – это множество элементов х, обладающих свойством ρ. Вместо вертикальной черты часто используется двоеточие. ρ(х) –это либо высказывание, в котором что-либо утверждается об х, либо это некоторая функция переменной х, например:
ρ(х)}, которое читается так: М – это множество элементов х, обладающих свойством ρ. Вместо вертикальной черты часто используется двоеточие. ρ(х) –это либо высказывание, в котором что-либо утверждается об х, либо это некоторая функция переменной х, например:
С помощью указанных средств не возможно сконструировать все возможные множества. Уже в самом задании конкретного множества явно или неявно ограничивается совокупность допустимых объектов.
Операции:
Множества можно определять также при помощи операций над некоторыми другими множествами.
Пусть имеются два множества: А и В.
1. Объединением (суммой) множеств А и В называется множество С, состоящее из всех элементов множества А и всех элементов В (в том числе и тех, которые принадлежат А и В). Символически эту операцию можно записать так: А  В={х
В={х  А
А 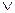 х
х  В}, здесь
В}, здесь 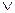 -«или».
-«или».
С=А+В=А  В, например А={1,2,3}; В={2,3,4}.
В, например А={1,2,3}; В={2,3,4}.
С= А  В={1,2,3,4}.
В={1,2,3,4}.

31)[2стр] 2. Пересечением множеств А и В называется множество С, состоящее из элементов, входящих одновременно в А и В. 
 , здесь
, здесь  - операция «И»
- операция «И»
если  ,то
,то  . Например,
. Например,  ,
,  ,
, 


Если  Ǿ., то такие множества называются непересекающимися.
Ǿ., то такие множества называются непересекающимися.
3. Разностью множеств А и В называется множество С, содержащее элементы множества А и не содержащее элементы множества В.  ,например:
,например:
 ;
;  ;
;
 ;
;
 .
.
Если  , то
, то 
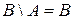 .
.

4. Симметрической разностью (дизъюнктивной суммой) называется множество С, элементы которого принадлежат либо А, либо В, но не обоим вместе (рис.5).
 =
= 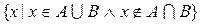 . Например,
. Например,  ;
;  ;
;
 .
.


5. Абсолютным дополнением множества А до универсального множества  называется множество, все элементы которого принадлежат
называется множество, все элементы которого принадлежат  и не принадлежат А.
и не принадлежат А.
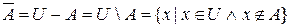 . (рис.6). Очевидно, что
. (рис.6). Очевидно, что  .
.
Дополнение А определяется отрицанием свойства 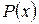 , с помощью которого определяется А.
, с помощью которого определяется А.

Рис.6.- Иллюстрация операции дополнение
Основные свойства алгебры множеств.
Операции над множествами обладают некоторыми свойствами, как и операции над числами, т.е. подчиняются следующим законам:
1. Коммутативный закон (переместительное свойство)
 ;
;  .
.
 ;
;
2. Ассоциативный закон (сочетательное свойство).
 ;
;  ;
;
 ;
;
3. Дистрибутивный закон (распределительное свойство)
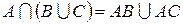 ;
;
 ;
;
4. Оригинальные операции:



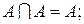
5. Закон поглощения:




6. Теорема де Моргана:
 ,
,
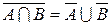
7.  ;
;  ;
;
8.  ;
;
