Коэффицие́нт асимметри́и в теории вероятностей — величина, характеризующая асимметрию распределения данной случайной величины.
Пусть задана случайная величина X, такая что E|X|3<∞. Пусть μ3 обозначает третий центральный момент: 
, а 
— стандартное отклонение X. Тогда коэффициент асимметрии задаётся формулой: 
.
Коэффицие́нт эксце́сса (коэффициент островершинности) в теории вероятностей — мера остроты пика распределения случайной величины.
Пусть задана случайная величина X, такая что E|X|4<∞.. Пусть μ4 обозначает четвёртый центральный момент: 
, а — стандартное отклонение X. Тогда коэффициент эксцесса задаётся формулой: 
.
Свойства коэффициента эксцесса
· 
.
· Пусть X1,X2,…,Xn— независимые случайные величины с равной дисперсией. Пусть 
. Тогда 
,где 
— коэффициенты эксцесса соответствующих случайных величин.
Коэффициент вариации случайной величины — мера относительного разброса случайной величины; показывает, какую долю среднего значения этой величины составляет ее средний разброс.
Равен отношению стандартного отклонения к математическому ожиданию.
Так же используется такие обозначение: 
Смысл коэффициента
В отличие от среднего квадратического или стандартного отклонения измеряет не абсолютную, а относительную меру разброса значений признака в статистической совокупности. Исчисляется в процентах. Вычисляется только для количественных данных.
Законы распределения дискретной случайной величины: биномиальное распределение. Параметры распределения. Математическое ожидание и дисперсия случайной величины, распределение по биномиальному закону.
Биномиа́льное распределе́ние в теории вероятностей— распределение количества «успехов» в последовательности из n независимых случайных экспериментов, таких что вероятность «успеха» в каждом из них равна P
Говорят, что с.в.Х имеет биномиальное распределение, если ее возможные значения равны 0,1,2…,к, …n, а соответствующие вероятности определяются по формуле (1).. Это название связано с тем, что 
равно коэффициенту при 
в разложении бинома
Возникает вопрос, какое максимальное значение принимает 
, если рассматривать , как функцию от k при фиксированном n? С этой целью рассмотрим отношение
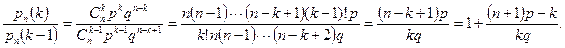
50)[стр2] Отсюда следует, что будет больше 
, если 
и меньше, если 
. Если 
- целое число, то Рn (m)=Рn (m-1). Это значит, что в двух точках достигается максимальное по k значение . Исключая эту ситуацию, имеем только одно целое число m, которое заключено в интервале
максимизирующее вероятность 
Распределение (1) зависит от двух параметров: 
и 
.
Рассмотрим числовые характеристики с.в., распределенной по биномиальному закону.
Математическое ожидание 
числа появления события А в n независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании: 
Очевидно, что общее число Х появлений события А в n испытаниях складывается из числа появления события А в отдельных испытаниях. Поэтому если Х1 число появлений события А в 1-м испытании, Х2 число появлений события А во 2-ом, Хn – в n 
-ом, то общее число появлений события А в n опытах будет равно:
Тогда 
, где
- математическое ожидание числа появления события А в i – ом опыте. Определим его 
Математическое ожидание числа появлений события в одном испытании равно вероятности этого события. Тогда
.
Дисперсия биномиального распределения с параметрами и равна произведению 
. 
.
Доказательство. По формуле дисперсии 
;
Поскольку Х1, Х2,…Хn независимы, то можно записать.
Определим 
;
; с вероятностью и 
:
; 
;
