Комбинаторика – это раздел математики, изучающий расположение объектов в соответствии с определёнными правилами и методы подсчёта всех возможных способов, которыми эти расположения могут быть сделаны.
Основное правило комбинаторики: Пусть требуется выполнить последовательно 
действий. Если первое действие можно выполнить 
способами, второе – 
способами, третье – 
способами, и так до -го действия, которое можно выполнить 
способами, то все действий вместе могут быть выполнены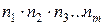 
способами
Перестановки, размещения.
Пусть W - множество, состоящее из 
элементов, из него можно образовать различные наборы (подмножества), состоящие из 
элементов, 
. Эти различные наборы (подмножества) могут быть перестановками, размещениями, сочетаниями.
Определение 1. Конечное множество называется упорядоченным, если каждому элементу этого множества поставлено в соответствие некоторое число (номер элемента) от 1 до , где - число элементов множества.
Всякое конечное множество (содержащее больше 1 элемента) можно упорядочить не единственным образом. Упорядоченные множества считаются разными, если они отличаются либо элементами, либо их порядком.
Определение 2. Различные упорядоченные множества, которые отличаются лишь порядком элементов (т.е. получены из того же самого множества), называются перестановками этого множества.
Пусть 
- число перестановок множества, содержащего элементов, имеет место равенство 
Определение 3. Размещением из элементов по , называется всякая упорядоченная часть множества, содержащая элементов.
Количество этих множеств легко посчитать, введя понятие выборки. Все множество элементов объёма (мощности ) будем называть генеральной совокупностью.
|
|
33)[стр2] Произвольное подмножество составленное из 
элементов генеральной совокупности 
назовём выборкой объёма . Возможны два случая выборки.
1. Размещения без повторений (выбор без возвращения). В этом случае каждый элемент генеральной выборки может встречаться не более одного раза в любой выборке.
Первый элемент выборки может быть выбран способами, второй - 
способами, и т. д., последний 
способом. Всего упорядоченных множеств объёма из множества объёма можно составить 
штук. Таким образом, число различных размещений из элементов по , которое обозначается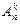 
будет равно
.
При 
2. Размещения с повторениями (выбор с возвращением).Размещение с повторениями - это такая выборка, в которой каждый элемент генеральной выборки объёма может встречаться любое число раз 
в каждой выборке объёма . Всего этих множеств будет 
. Иногда используется обозначение 
. Запишем всевозможные размещения с повторениями из множества 
по два элемента:
, всего 9 элементов, т.е. 
.
Сочетания.
Определение 5. Две неупорядоченные выборки объёма будем считать различными, если в одной из них содержится элемент, не содержащийся в другой.
Определение 6. Сочетаниями из элементов по называются различные выборки объёма из генеральной совокупности объёма .
Число различных выборок объёма k из генеральной совокупности, состоящей из n элементов, называется числом сочетаний из n по k элементов и обозначается 
. Выведем для определения этого числа формулу.
1. Сочетания без повторений. Мы знаем, что из генеральной совокупности объёма n можно 
способами получить упорядоченные выборки объёма k. По определению - число различных выборок объёма k, образованных из n элементов. Чтобы получить упорядоченные выборки на каждой из выборок нужно сделать все возможные перестановки, число таких перестановок 
. Тогда можно записать 
; 
.
|
|
Если выразить через факториалы, то 
.
Числа называются биномиальными коэффициентами: 
- биномиальная формула. Имеет место важное свойство биномиальных коэффициентов:
;
;
.
2. Сочетания с повторениями.
Определение 7. Сочетаниями из n элементов по k с повторениями, называются различные выборки объёма k из генеральной совокупности объёма n, в которых каждый элемент генеральной выборки может встречаться любое число раз .
;
Число сочетаний с повторениями, в которых каждый элемент представлен хотя бы один раз равно: 
.