1.Аксиоматический способ задания вероятностей.
Рассмотрим эксперимент, с конечным или счетным числом возможных исходов W={w1, w2, w i … }. Предположим, что каждому элементарному событию w i приписан некоторый ''вес'' p i, называемый вероятностью появления элементарного события w i, и потребуем, чтобы вероятность p i удовлетворяла следующим условием:
1)0£p(w i)£1 – неотрицательность
2)  ; - нормированость.
; - нормированость.
Для данного эксперимента построена вероятностная модель, если указано пространство элементарных событий W: 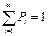 ; и известна вероятность элементарного события Р(w i), Р i ³ 0;
; и известна вероятность элементарного события Р(w i), Р i ³ 0; 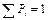 ,w i ÎW.
,w i ÎW.
Пусть А – произвольное случайное событие, наблюдаемое в данном эксперименте т.е. А Ì W. Тогда имеет место следующее определение.
Определение: Вероятностью события А называют сумму вероятностей элементарных событий, составляющих событие А:
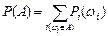 .
.
Из определения вероятности события P(A) вытекают следующие свойства вероятности:
0£P(A); - аксиома неотрицательности;
P(W)=1; - аксиома нормировки;
Аксиома адитивности (сложения):
Если А иВ несовместные события (А Ì W, В Ì W,А·В= Æ), то Р(А+В)=Р(А)+Р(В).
Эти аксиомы были сформулированы А.Н.Колмогоровым и оказали огромное влияние на развитие теории вероятностей..Такое задание вероятности события называются аксиоматическим.
Аксиома аддитивности может быть расширена на случай n попарно несовместимых событий, т.е.
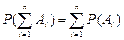 , A i ÎW; Ai·A j =Æ; i,j =
, A i ÎW; Ai·A j =Æ; i,j = 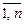 , i¹j.
, i¹j.
Вероятность суммы несовместимых событий равна сумме вероятностей этих событий.
Аксиому сложения вероятностей иногда называют теоремой сложения вероятностей, или правилом сложения вероятностей.
Если имеется счетное множество несовместимых событий А1,А2…Аn… (Ai·A j =Æ; i¹j) то 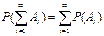 ;
;
Следствия из аксиом теории вероятностей:
Следствие 1: Если А Ì В, (влечении В), то Р(А)<Р(В).
Следствие 2: Р( )=1-Р(А); А+
)=1-Р(А); А+  =W; по аксиоме 3, А·
=W; по аксиоме 3, А·  =Æ,
=Æ,
Р(А)+Р(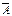 )=Р(А+
)=Р(А+  )=Р(W)=1;
)=Р(W)=1;
Следствие 3: Р(Æ)=0;
38)[стр2] Следствие 4: Если А и В совмесимые события, наблюдаемые в одном и том же пространстве элементарных событий, W, тогда
Р(А+В)=Р(А)+Р(В)-Р(А·В).
Замечание 1: Если имеется три совместных события А,В,С, связанных с одним и тем же испытанием, то можно показать, что
Р(А+В+С)=Р(А)+Р(В)+Р(С)-Р(А·В)-Р(А·С)-Р(В·С)+Р(А·В·С).
Замечание 2: Вероятность суммы событий в случае, когда число слагаемых больше 2-х, целесообразно вычислять переходом к противоположному по отношению к сумме событию.
Вывод: Аксиомы теории вероятностей позволяют вычислять вероятности любых случайных событий через вероятности элементарных событий, если их число конечно или счетно. Но теория вероятностей ''не учит'' тому, как правильно определять вероятности элементарных событий. На практике они определяются либо непосредственно по условиям опыта (если он обладает симметрией возможных исходов), либо на основе экспериментальных статистических данных, (если он такой симметрией не обладает).
2. Класический способ задания вероятностей.
Если элементарное событие wi равнозначны, т.е. Р(wi)=Р, (wi имеют одинаковый вес) и А={wi1,wi2,…,wim}, iÎI, W={w1,w2,…,wn}, то Р(W)=  ;
;
тогда Р(w i)=Р·1/n; и Р(А)=  .
.
При классическом подходе к определению вероятности вероятность события А можно трактовать как отношение исходов (элементарных событий) благоприятствующих появлению события А к общему числу равнозначных исходов. Классическое определение вероятностейоправдано тогда, когда на основании симметрии, однородности и т.п. можно говорить о равнозначных исходах или равнозначных событиях.
3. Статистическая вероятность
Наряду с классическим определением вероятности, которое базируется на понятии «равнозначности события» и применимо к конечному числу элементарных событий, используется понятие статистической вероятности. В качестве статистической вероятности принимают частоту появления события А при проведении многократных испытаниях. Пусть в результате n (n>>1) испытаний событие А появилось m раз, тогда статистическая вероятность
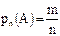
и получаем свойства:
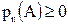 ,
, 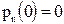 ,
, 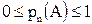 ,
,  .
.
Английский математик Пирсон бросал монету 24000 раз. «Герб» выпадал 12012 раз, а значит статистическая вероятность выпадения «герба» (событие А) была равной
 .
.
Недостаток этого определения при всей его привлекательности заключается в неоднозначности этого определения, т.е. в зависимости вероятности от числа испытаний. Другой статистический подход в определении вероятности заключается в том, что в качестве вероятности берут предел частоты появления события А при неограниченном числе испытаний:
 .
.
Однако такой подход трудно реализовать на практике, так как невозможно произвести бесконечное число испытаний.
4. Геометрическая вероятность.
Если число равновозможных элементарных событий бесконечно, то использовать классическое определение вероятности невозможно. Однако, в таких ситуациях иногда можно воспользоваться методом геометрической вероятности. Суть метода заключается в случайном бросании точки на ограниченый участок либо прямой, либо плоскости, либо пространство. Если брошенная точка обязательно попадет в неограниченную область W, содержащую область А (А Ì W), и вероятность попадания в любую часть W не зависит от формы этой части и пропорциональна её мере (длине, площади, объему), то вероятность попадания точки в область А равна отношению мер областей А и W:
 .
.