Функция распределения случайной величины, ее свойства. Функция распределения дискретной и непрерывной случайной величины.

Если имеется непрерывная случайная величина Х, то описать ее с помощью ряда распределения невозможно, т.к. вероятность принятия ею какого-либо конкретного значения равна нулю. Для непрерывной случайной величины вводится понятие функции распределения вероятностей.

Функцией распределения вероятностей F(x) или интегральным законом распределения случайной величины Х называется вероятность того, что случайная величина Х примет значение меньше х:

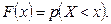
функция распределения это вероятность того, что случайная величина Х примет любое значение левее точки с абсциссой х. Функция распределения существует как для непрерывных, так и для дискретных случайных величин. Для дискретных величин она имеет ступенчатую структуру.

Из определения функции распределения вероятностей следуют следующие ее свойства:

;

;

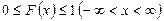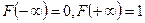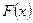не уменьшается при возрастанием х;

Дискретные распределения

Случайная величина называется простой или дискретной, если она принимает не более, чем счётное число значений. То есть 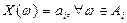, где 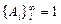- разбиение Ω.

Распределение простой случайной величины тогда по определению задаётся: 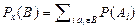. Введя обозначение p_i=P(A_i), можно задать функцию p (a_i) = p_i. Очевидно, что 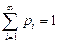. Используя счётную аддитивность P, легко показать, что эта функция однозначно определяет распределение X.

Функция p (a_i) = p_i, где 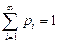называется дискретным распределением.

Дискретное распределение обладает следующими свойствами:

1. ;

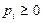2. .

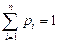Различия между функциями распределения вероятностей дискретной и непрерывной случайных величин хорошо иллюстрировать графиками. Пусть, например, дискретная случайная величина имеет n возможных значений, вероятности которых равны P{X=x_k}=p_k, k=1,2,..n. Если x ≤ x₁, то F(Х)=0, так как левее х нет возможных значений случайной величины. Если x₁< x ≤ x₂, то левее х находится всего одно возможное значение, а именно, значение х₁.

44)[стр2]

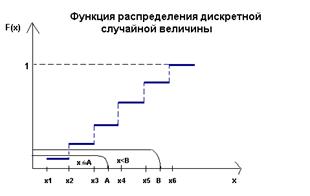
Значит, F(x)=P{X=x₁}=p₁.При x₂< x ≤ x₃ слева от х находится уже два возможных значения, поэтому F(x)=P{X=x₁}+P{X=x₂}=p₁+p₂. Рассуждая аналогично,приходим к выводу, что если х_k< x≤ x_k+1, то F(x)=1, так как функция будет равна сумме вероятностей всех возможных значений, которая по условию нормировки равна еденице. Таким образом, график функции распределения дискретной случайной величины является ступенчатым. Возможные значения непрерывной величины располагаются плотно на интервале задания этой величины, что обеспечивает плавное возрастания функции распределения F(x), т.е. ее непрерывность.

Рассмотрим вероятность попадания случайной величины в интервал [x, x+Δx], Δx>0: P{x≤X< x+Δx}=F(x+ Δx)-F(x). Перейдем к пределу при Δx→0:

lim_(Δx→0)P{x≤ X < x+Δx}=lim_(Δx→0)F(x+Δx)-F(x). Предел равен вероятности того, что случайная величина примет значение, равное х. Если функция F(x) непрерывна в точке х, то lim_(Δx→0)F(x+Δx)=F(x), т.е. P{X=x}=0.

Если F(x) имеет разрыв в точке х, то вероятность P{X=x} будет равна скачку функции в этой точке. Таким образом, вероятность появления любого возможного значения для непрерывной величины равна нулю. Выражение P{X=x}=0 следует понимать как предел вероятности попадания случайной величины в бесконечно малую окрестность точки х при P{Α< X≤ Β},P{Α ≤ X< Β},P{Α< X< Β},P{Α ≤ X≤ Β} равны, если Х - непрерывная случайная величина.

Для дискретных величин эти вероятности неодинаковы в том случае, когда границы интервала Α и(или) Β совпадают с возможными значениями случайной величин. Для дискретной случайной величины необходимо строго учитывать тип неравенства в формуле P{Α ≤X<Β}=F(Β)-F(Α).