1. Условная вероятность события
В ряде случаев приходится рассматривать вероятности случайных событий, в предположении, что произошло некоторое случайное событие.
Пусть пространство элементарных событий состоит из n одинаково возможных элементарных событий, событию А благоприятствует m элементарных событий, событию В состоит из l исходов, событию А·В благоприятствует ч исходов.
 ;
;
Если произошло событие В, то произошло одно из l элементарных событий. Событие А произойдет только тогда, когда произойдет одно из ч событий, т.е.
 ;
;
Определение: Условной вероятностью события А при условии, что произойдет событие В называют
 , (5.1)
, (5.1)
Из этого определения следует что вероятность события А/В можно рассматривать, как вероятность события АВ с нормировкой Р(В).
Отсюда следует, что условная вероятность обладает всеми свойствами вероятности:
0 £ p(A/B) £1;
p(A/A)=1 (p(0/A)=0);
p((A1+A2)/B)=p(A1/B)+p(A2/B) (если р(А1А2)=0).
Формулу (5.1) можно рассматривать в виде
P(AB)=P(A/B)*P(B) (теорема умножения).
Теорема умножения Вероятность произведения (пересечения, совмещения) двух событий равна вероятности одного из них, умноженной на условную вероятность второго при наличии первого
Т.е. вероятность произведения нескольких событий равна произведению вероятностей этих событий, причем вероятность каждого последующего события вычисляется при условии, что все предыдущие имели место
2. Формула полной вероятности.
Следствием обоих основных правил теории вероятности (правила сложения и правила умножения) – является формула полной вероятности.
Допустим, что предполагается провести опыт, об условиях которого можно сделать n исключающих друг друга предположений (гипотез).
Пусть гипотезы H1, H2,…, Hn образуют полную группу попарно несовместимых событий, т.е.
W= H1+ H2+… + Hn (Hi Hj=0, i¹j).
Каждая гипотеза осуществляется случайным образом и представляет собой некоторое событие. Вероятности гипотез известны и равны Р(H1),Р(H2),…,р(Hn).
Рассматривается некоторое событие А, которое может проявиться только вместе с одной из гипотез, заданы условные вероятности Р(А/Н i) события А при каждой из гипотез. Требуется найти вероятность события А. Представим событие А следующим образом:
А=АW=А(H1+ H2+… + Hn)= АH1+ АH2+… + АHn.
Так как события АH1, АH2,…, АHn также несовместимы, то используя правила сложения и умножения вероятностей, получим формулу полной вероятности:
Р(А) = р(АH1)+р(АH2)+…+р(АHn)=р(А/H1)р(В1)+р(А/H2)р(H2)+…+ р(А/Вn)р(Вn),
 .
.
Безусловная вероятность события А в опыте с гипотетическими условиями вычисляется как сумма произведений вероятностей каждой гипотезы на условную вероятность события А при этой гипотезе.
Формула полной вероятности применяется во всех случаях, когда опыт со случайным исходом распадается на два этапа: в первом как бы ''разыгрываются'' условия опыта; во втором – его результат.
3. Формула Байеса (теорема гипотез).
Следствием правил умножения и формулы полной вероятности является теорема гипотез или формула Байеса.
Представим себе следующую ситуацию. До опыта о его условиях можно было сделать ряд гипотез Н1, Н2,…,Нn, несовместимых и образующих полную группу
 Æ; (i ¹ j);
Æ; (i ¹ j);
39)[стр2] Вероятность гипотез до опыта (априорные вероятности) заданы и равны: Р(H1), Р(H2),…, Р(Hn);  ;
;
Теперь предположим, что опыт произведен, и в его результате появилось событие А. Спрашивается, как нужнопересмотреть вероятность гипотез, с учетом этого факта. Т.е. необходимо найти ''апостериорные вероятности'' гипотез, при условии, что опыт дал результат А, т.е Р(Н1/А); Р(Н2/А)… Р(Н i /А).
Решим эту задачу,используя правило умножения и формулу полной вероятности:
Возьмем любую гипотезу Н i и вычислим вероятность Р(Н i ·А) по правилу умножения в двух формах:
Р(Hi·A)= Р(Hi)· Р(A/Hi)=P(A)· Р(Hi/A);
Р(Hi)· Р(A/Hi)=P(A)· Р(Hi/A).
Разделим обе части на Р(А)¹0, т.е. 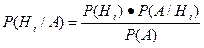 .
.
Заменим Р(А) его выражением из формулы полной вероятности, получим формулу Байеса:
 .
.